5.20: Solutions to Selected Problems
- Page ID
- 191275
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
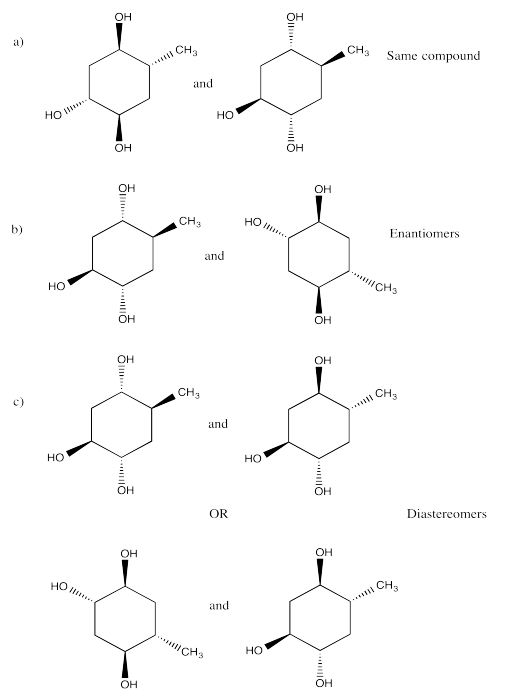
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 5.2.1:
Exercise 5.2.2:
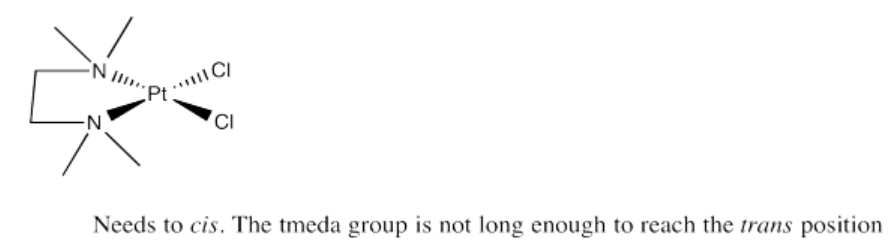
Exercise 5.3.1:
Clockwise.
Exercise 5.3.2:
Counter-clockwise.
Exercise 5.3.3:
Counter-clockwise.
Exercise 5.3.4:
Clockwise.
Exercise 5.3.5:
Enantiomer B has a molecular weight of 126 g/mol, a density of 0.995 g/mL, an optical rotation of [α] = – 26°, a melting point of 65°C and a boiling point of 225°C.
Exercise 5.3.6:

Exercise 5.3.7:
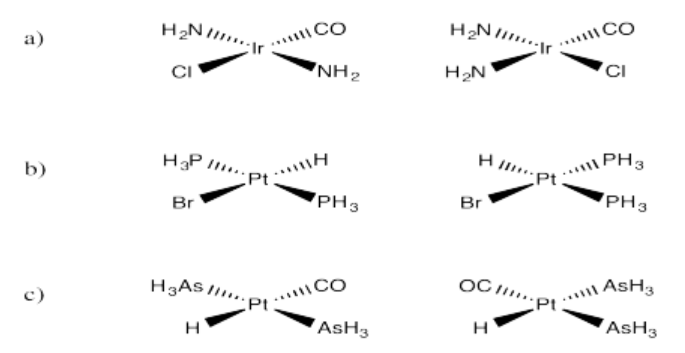
A. The plane of the page is a mirror plane. There is also one perpendicular to the page that reflects one H into the other.
B. The plane of the page contains one P-Cl bond and bisects the other Cl’s.
C. The plane of the page is a mirror plane.
D. Mirror plane contains P-Br bond and bisects the Cl’s.
E. There is no lone pair on the B. Therefore all atoms lie in a mirror plane.
F. No mirror planes--the molecule is therefore chiral.
G. There is a plane perpendicular to the page that contains the Br and Cl and bisects the cyclopropane ring.
H. No mirror planes--the molecule is therefore chiral.
I. There is a plane perpendicular to the page that contains the Br and Cl and bisects the cyclopropane ring.
J. The C-C bond can be rotated by 60 degrees so that there is a plane perpendicular to the C-C bond axis.
K. The C-C bond in one of the chlorine-containing arms can be rotated so that there is a mirror plane that goes through the ethyl group (with no Cl’s) and the P, and one chlorine containing arm is the reflection of the other.
L. Since a double bond is planar, there is a mirror plane that contains all six atoms.
M. There is a mirror plane that contains two C’s and bisects the two Cls.
N. No mirror planes--the molecule is therefore chiral. The rings are not in the same plane due to the CH3 and NH2 groups, which bump into each other. They also prevent rotation around the C-C bond between the rings.
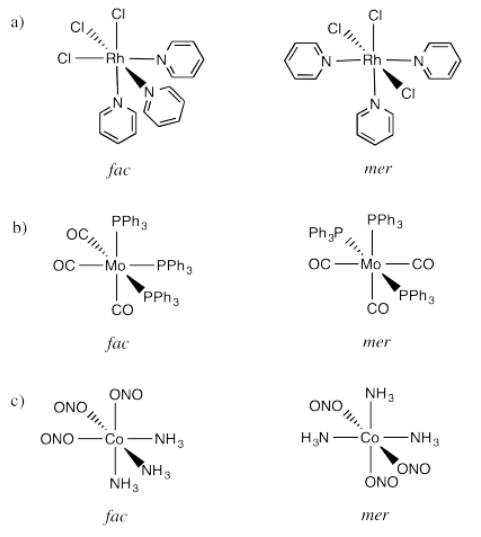
Exercise 5.3.8
Picture (a)
Exercise 5.3.9:
Picture (b)
Exercise 5.3.10:
Picture (d)
Exercise 5.3.11:
Picture (c)
Exercise 5.4.1:
Priority of groups:
1 Br (red)
2 Cl (bright green)
3 F (pale green)
4 H (white)
In the molecule in figure 5.4.2, with the low-priority hydrogen pointed away, bromine is at the top, chlorine is clockwise from the bromine, and fluorine is clockwise from the chlorine. It therefore has an assigned configuration of R.
In the molecule in figure 5.4.3, with the low-priority hydrogen pointed away, bromine is at the top, chlorine is counterclockwise from the bromine, and fluorine is counterclockwise from the chlorine. Thus, it has an assigned configuration of S.
Exercise 5.4.2
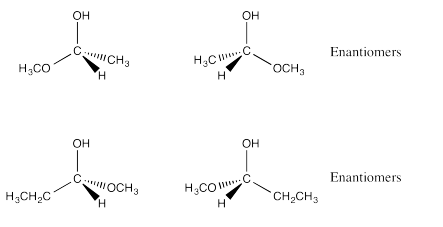
Exercise 5.4.3:
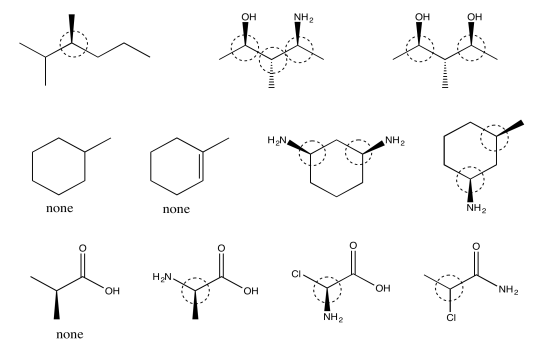
Exercise 5.4.4:
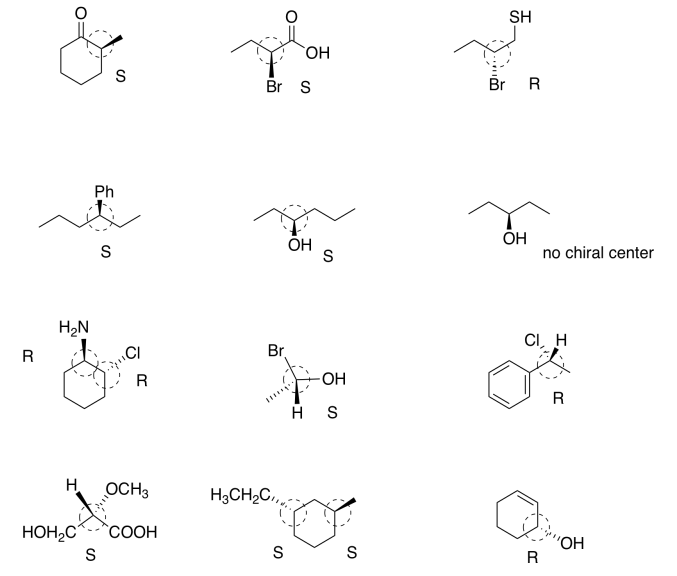
Exercise 5.4.5:

Exercise 5.4.6:
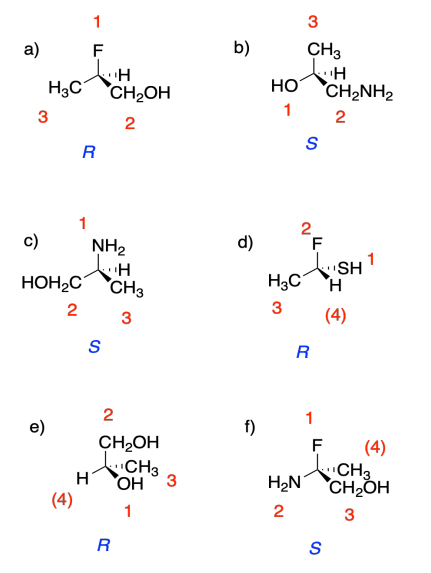
Exercise 5.5.1:
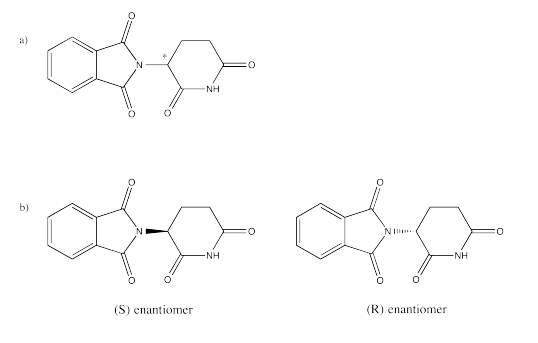
Exercise 5.5.2:

Exercise 5.5.3:
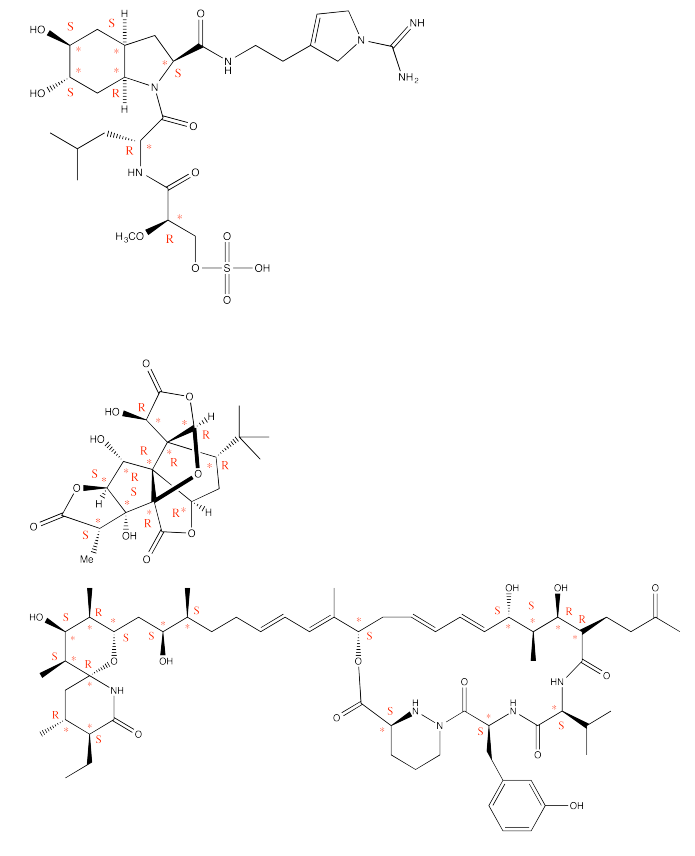
Exercise 5.6.1:
A pure sample of A would have \([\alpha] = 75^{\circ}\)
Optical purity or enatiomeric excess = \(\frac{50}{75} = 66 \% \)
% major enantiomer = \(66 + \frac{34}{2} = 83 \% \)
% minor enantiomer = \(100 - 83 = 17 \%\)
Exercise 5.6.2
\[ \% \: major \: = 90 \% \nonumber\]
\( \% \: major \: = 10 \%\)
Optical purity or enantiomeric excess = \( \frac{X}{-50} = 90-10 = 80 \% \)
Solve for X. \(X = -40^{\circ}\)
Exercise 5.6.4:
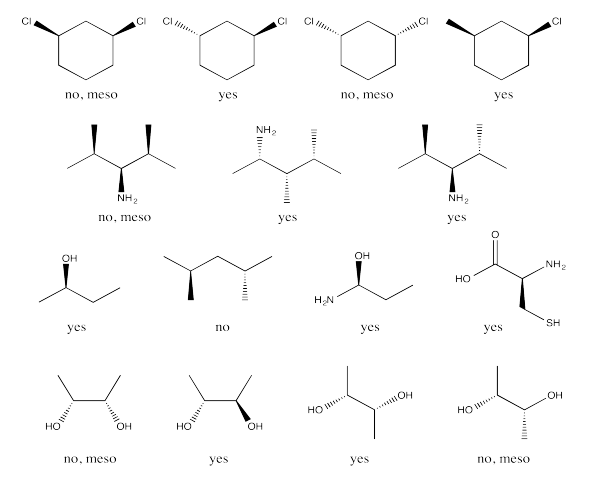
Exercise 5.7.1:
a) \([\alpha] = \frac{\alpha}{(c)(l)}\)
\(c = (\frac{0.250g}{2mL})(\frac{10mL}{1dL}) = 1.25 \frac{g}{dL}\)
\(\alpha = \frac{(0.775 ^{\circ} + 0.806 ^{\circ} + 0.682 ^{\circ})}{3} = 0.754 ^ {\circ} \)
\([\alpha] = \frac{\alpha}{(c)(l)} = \frac{(0.754 ^{\circ})}{(1.25 \frac{g}{dL})(0.5dm)} = + 1.21 ^{\circ}\)
b)
– 1.21°
Exercise 5.7.2:
\[[\alpha] = \frac{\alpha}{(c)(l)} \nonumber\]
\([\alpha] = 32 \circ\)
\(c = (\frac{0.150g}{1mL})(\frac{10mL}{1dL}) = 1.5 \frac{g}{dL}\)
c = (0.150g/ 1 mL)(10 mL/1 dL) = 1.5g/dL
\([\alpha] = \frac{\alpha}{(c)(l)} = 32 ^{\circ} = \frac{\alpha}{(1.5 \frac{g}{dL})(0.5dm)}\)
Solve for α. \( \alpha = + 24^{\circ}\)
Exercise 5.8.1:
D-glyceraldehyde is R
L-glyceraldehyde is S
Exercise 5.8.2:
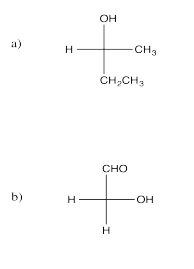
Exercise 5.8.3:
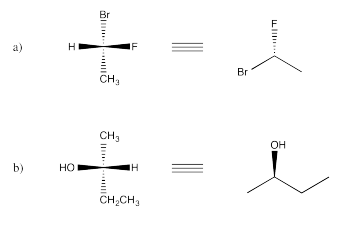
Exercise 5.9.1:
a) left b) right
Exercise 5.9.2:
a) right b) left
Exercise 5.9.1:
a) right b) right
Exercise 5.9.2:
a) left b) left
Exercise 5.9.5:
D-threose
2S, 3R
Exercise 5.9.6:
L-threose
2R, 3S
D- and L-threose are enantiomers of one another
Exercise 5.9.7:
L-erythrose
2S, 3S
L-erythrose and L-threose are diastereomers of one another.
Exercise 5.9.8:
a) (2)3 = 8 possible stereoisomers
RRR; SSS; RRS; SSR; RSS; SRR; SRS; RSR
b) 4 pairs
c) 12 different possible pairs of diastereomers
Exercise 5.9.9:
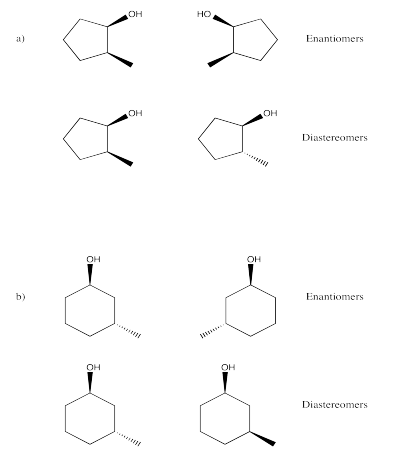
Exercise 5.9.10:
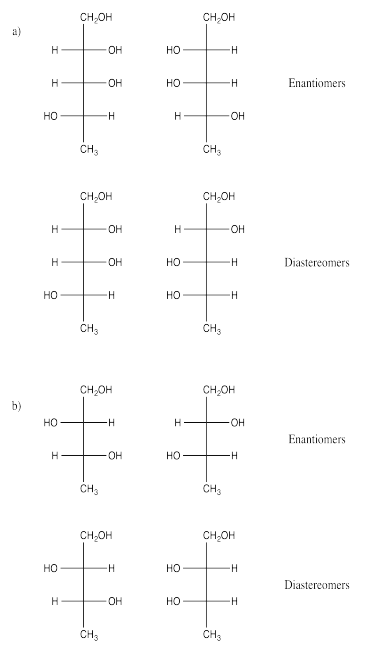
Exercise 5.10.1:
a) D-threitol → 2R, 3S
b) L- threitol → 2S, 3S
c) erythritol → 2S, 3R or 2R, 3S (a meso compound)
Exercise 5.10.2:
It does not matter which end you start counting from on these compounds since they are constituted the same.
Exercise 5.10.3:
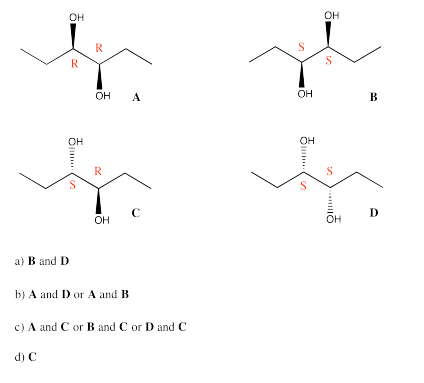
Exercise 5.10.4:
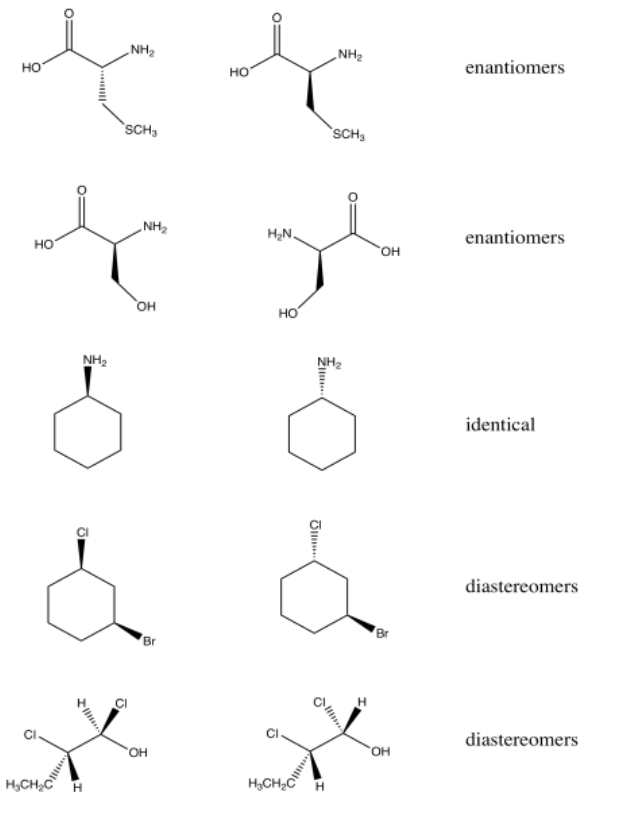

Exercise 5.11.1:
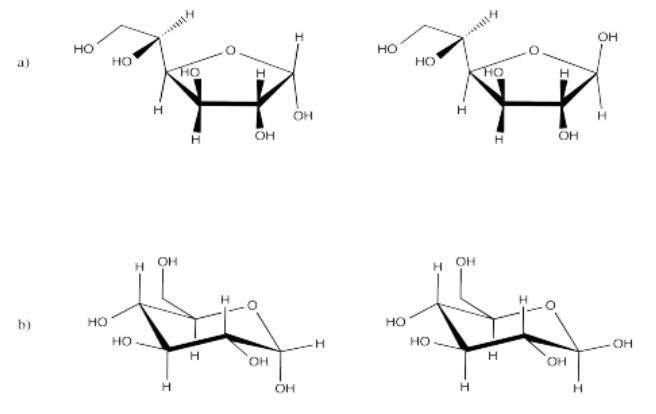
Exercise 5.11.2:
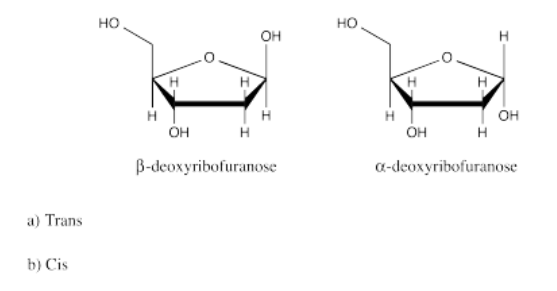
Exercise 5.12.1:
Glycine
Exercise 5.12.2:
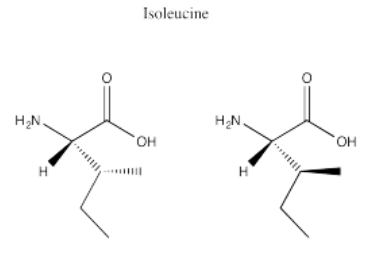
Exercise 5.12.3:
Proline
Exercise 5.12.4:
Glutamic acid and aspartic acid
Exercise 5.12.5:
Arginine, asparagine, glutamine, lysine; also tryptophan contains an aromatic heterocycle, although it is not basic.
Exercise 5.12.6:
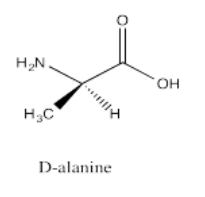
Exercise 5.12.7:
Cysteine
Exercise 5.13.1:
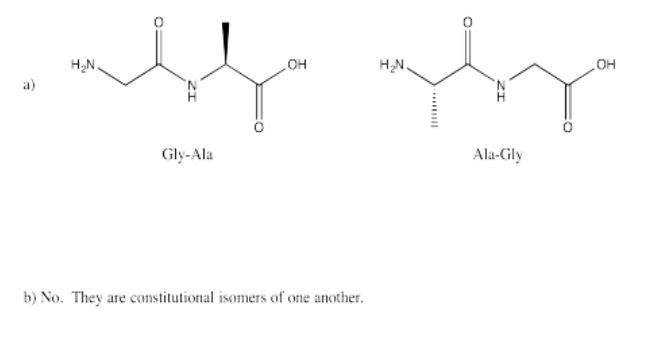
Exercise 5.13.2:
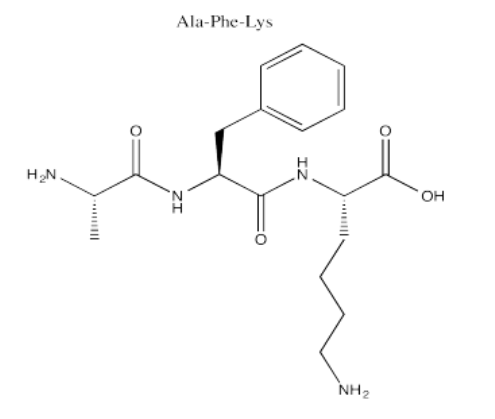
Exercise 5.14.1:
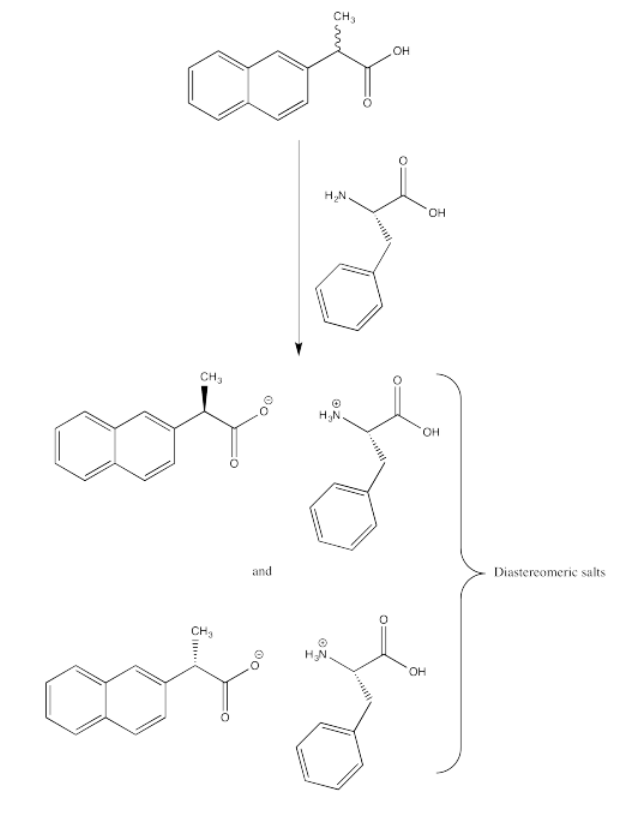
Exercise 5.15.1:
A. Cis
B. Trans
C. Trans
D. Neither (There is free rotation around the C-C single bond.)
E. Neither (C-C triple bonds have substituents at 180 degrees to each other (linear).
F. cis
Exercise 5.16.1:
A. Z
B. E
C. E
D. Z
E. E
F. E
G. Z
H. E
Exercise 5.17.1:
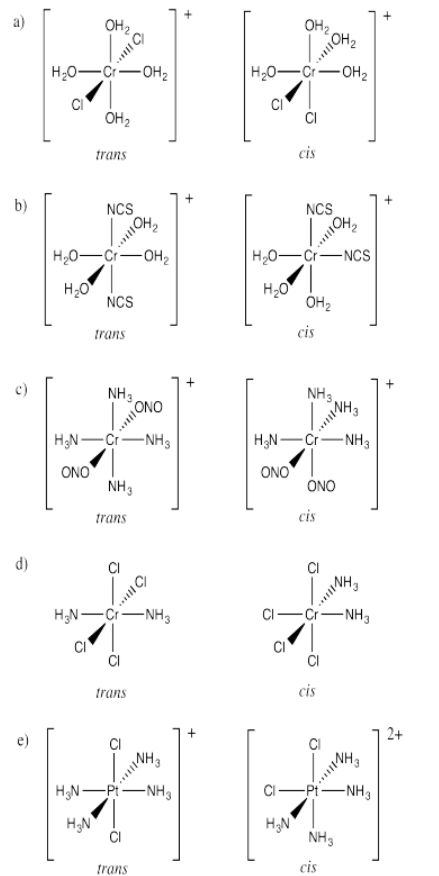
Exercise 5.17.2:
Exercise 5.18.1:
a) Enantiomers
b) Enantiomers
c) Identical
d) Identical
e) Enantiomers
f) Identical
g) Enantiomers
Exercise 5.18.2:
a) Δ b) Λ c) Δ d) Λ e) Δ f) Δ g) Λ h) Λ
Exercise 5.20.1:
Pure = 125°
Optical purity = \(\frac{100}{125} = 0.80\)
\[\% \: Major \: = 80 + \frac{20}{2} = 90\% \nonumber\]
\[\% \: Minor \: 100-90 = 10 \% \nonumber\]
Exercise 5.20.2
Pure = 100°
Optical purity = \(\frac{95}{100} = 0.95\)
\(\% \: Major \: = 95 + \frac{5}{2} = 97.5 \%\)
\[\% \: Minor \: 100-97.5=2.5 \% \nonumber\]
Exercise 5.20.3
\[Pure \: = 18^{\circ} \nonumber\]
\[\% \: Major \: = 60 \% \nonumber\]
\(\% \: Minor \: = 40 \% \)
Optical purity = \(\frac{X}{18} = 20 \%\)
Solve for X:
\[X = 3.6^{\circ} \nonumber\]
Exercise 5.20.4:
\[Pure \: = 25^{\circ} \nonumber\]
\[ \% Major \: = 80 \% \nonumber\]
\( \% Minor \: = 20 \% \)
Optical purity = \(\frac{X}{25} = 80-20= 60 \%\)
Solve for X:
\[X = 15^{\circ} \nonumber\]
Exercise 5.20.5
\[[\alpha] = \frac{observed \: rotation}{(l)(c)} \nonumber\]
\(c = \frac{0.050g}{2.0mL} = 0.025 \frac{g}{mL}\)
Average observed rotation = \(\frac{(0.625 + 0.706 + 0.682)}{3} = 0.671 ^{\circ}\)
\[[\alpha] = \frac{0.671 ^{\circ}}{(0.025 \frac{g}{mL})(0.5 dm)} = 53.68 ^{\circ} \nonumber\]
Exercise 5.20.6:
\[[\alpha] = \frac{observed \: rotation}{(l)(c)} \nonumber\]
\(c = \frac{0.540g}{2.0mL} = 0.27 \frac{g}{mL}\)
Average observed rotation = \(\frac{(1.225 + 1.106 + 1.182)}{3} = 1.171 ^{\circ} \)
\[[\alpha] = \frac{1.171 ^{\circ}}{(0.27 \frac{g}{mL})(1.0 dm)} = 4.34 ^{\circ} \nonumber\]
Exercise 5.20.7:
\[[\alpha] = \frac{observed \: rotation}{(l)(c)} \nonumber\]
\[c = \frac{0.250g}{2.0mL} = 0.125 \frac{g}{mL} \nonumber\]
\(42 ^{\circ} = \frac{observed \: rotation}{(0.125 \frac{g}{mL})(0.5dm)}\)
observed rotation = 2.625°
Exercise 5.20.8
a) \([\alpha] = \frac{observed \: rotation}{(l)(c)}\)
\[c = \frac{0.10g}{2.0mL} = 0.05 \frac{g}{mL} \nonumber\]
\(c = \frac{0.10g}{2.0mL} = 0.05 \frac{g}{mL}\)
Average observed rotation = \(\frac{(0.995 + 0.904 + 0.936)}{3} = 0.945 \circ \)
\([\alpha] = \frac{0.945 ^{\circ}}{(0.05 \frac{g}{mL})(1.0 dm)} = 18.9 \circ \)
b) % optical purity = \(\frac{(100)(18.9)}{25}= 75.6 \%\)
c) enantiomeric excess = 75.6%
d) \(\frac{(100-75.6)}{2} = 12.2 \%\)
12.2 % one enantiomer
87.8% other enantiomer
e) Enantiomers differ in how they interact with plane polarized light, but not in other physical analyses.
Exercise 5.20.9
\[[\alpha] = \frac{observed \: rotation}{(l)(c)} \nonumber\]
\[40 \circ = \frac{observed \: rotation}{(l)(c)} \nonumber\]
\(40 \circ = \frac{observed \: rotation}{(l)(1.1c)}\)
Observed rotation = 44°
Exercise 5.20.10
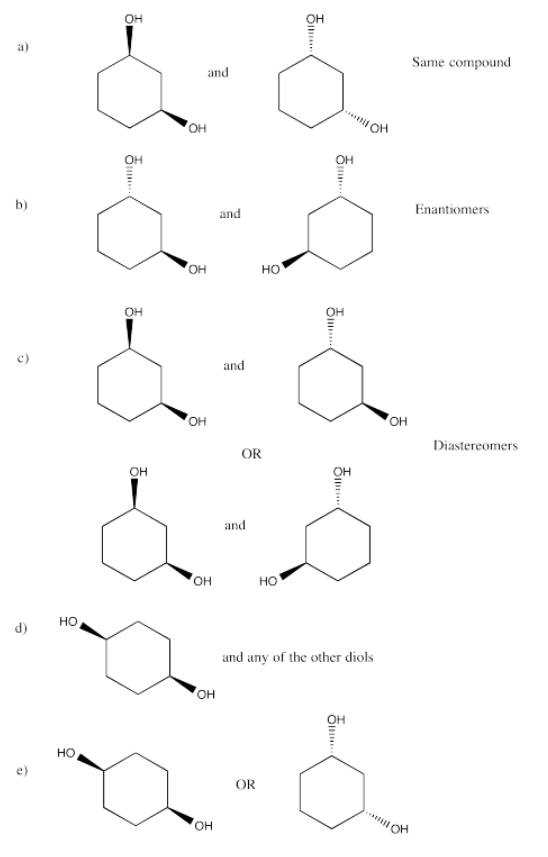
Exercise 5.20.11:
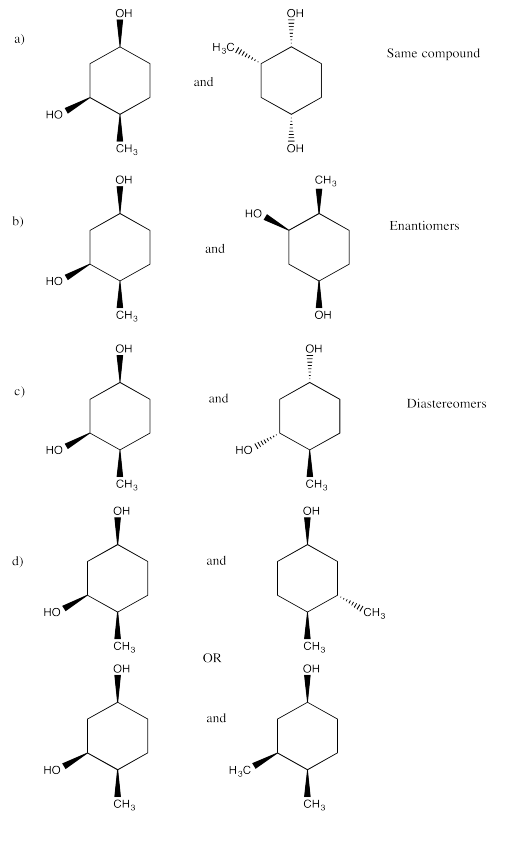
Exercise 5.20.12: