5.18: Enantiomers in Octahedral Complexes
- Page ID
- 191242
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Enantiomers are another kind of isomer that occur in octahedral metal complexes. Like the square planar platinum complexes seen before, these compounds consist of metal ions with other atoms or groups bound to them. More information about the binding of ligands to metals is found in the section on Lewis acids and bases.
These groups that bind to metal ions are called ligands. One example of a type of octahedral compounds that can form enantiomers is bidentate complexes. In bidentate complexes (from the Greek two teeth) or chelating complexes (from the Greek crab), a ligand binds very tightly to the metal because it holds onto the metal via more than one atom. Ethylenediamine is one example of a bidentate ligand.
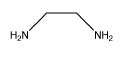
- Bidentate ligands bind very tightly to a metal because they form two bonds with it, rather than just one.
- In an octahedral complex, the two donor atoms in a bidentate ligand bind cis to each other. They can't reach all the way around the molecule to bind trans to each other.
The spatial relationship between the metal and the two atoms connected to it from the same ligand forms a plane. If more than one bidentate ligand is connected to the metal, the relative orientation of one plane to another creates the possibility of mirror images. A complex containing three bidentate ligands can take on the shape of a left-handed propeller or a right-handed propeller.
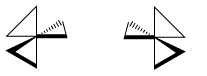
If you turned this propellor, in what direction would the air be pushed? Maybe it is an airplane propellor or maybe it is a fan blade. If you turned a lambda fan blade counter-clockwise, it would blow cool air on you. You would have to turn a delta fan clockwise to cool off.

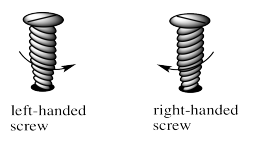
These shapes are alternatively described as a left-handed screw and a right handed screw. If you want to screw a right-handed screw into a floor, you turn the screwdriver clockwise. If you want to screw a right-handed screw into a floor, you turn the screwdriver counterclockwise. Screws are chiral in much the same way that a helix is chiral. The threads on the screw cycle either clockwise or counterclockwise as they run down the length of the screw.
If you can picture turning the "delta" or "lambda" propellor shape so that it screws into the page behind it, which direction would you turn it?

You would turn the lambda screw counter-clockwise to send it into the page behind it. You would have to turn the delta screw the opposite way; turning it clockwise would send it into the page.
Examples of this enantiomeric relationship include cobalt complexes of bidentate ligands.
Go to Animation SC17.3. A three-dimensional model of Δ-Co(en)3.
Go to Animation SC17.3. A three-dimensional model of Λ-Co(en)3.
These relationships are also seen when there are just two bidentate ligands in the compound.
Go to Animation SC17.3. A three-dimensional model of ΛCo(en)2(NH3Cl.
Go to Animation SC17.3. A three-dimensional model of ΔCo(en)2(NH3Cl.
What do we know about enantiomers?
- enantiomers have identical physical properties, except...
- enantiomers have opposite optical rotation.
These kinds of complexes were historically important in demonstrating how small molecules and ions bound to metal cations. By showing that some metal complexes were chiral and displayed optical activity, early 20th century workers such as Alfred Werner were able to rule out some competing ideas about the structures of metal compounds.
Today, we know that metal complexes play important roles in enzymes in biology, and Werner's work on metal complexes laid the groundwork for how we think about these complexes.
In addition, stereochemistry in metal complexes became very important in the late 20th century, especially as pharmaceutical companies looked for catalysts that could aid in the production of one enantiomer of a drug, and not the other, in order to maximize pharmaceutical effectiveness and minimize side effects.
Exercise \(\PageIndex{1}\)
Identify the relationships between the following pairs of iron(III) oxalate ions.
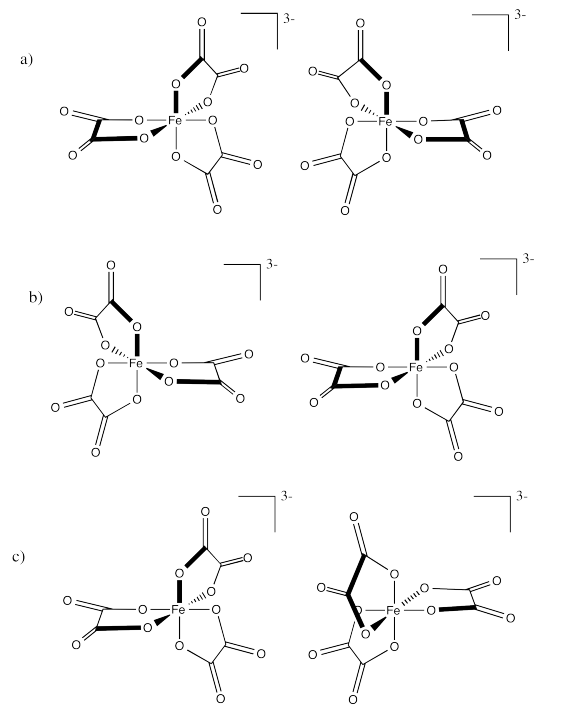
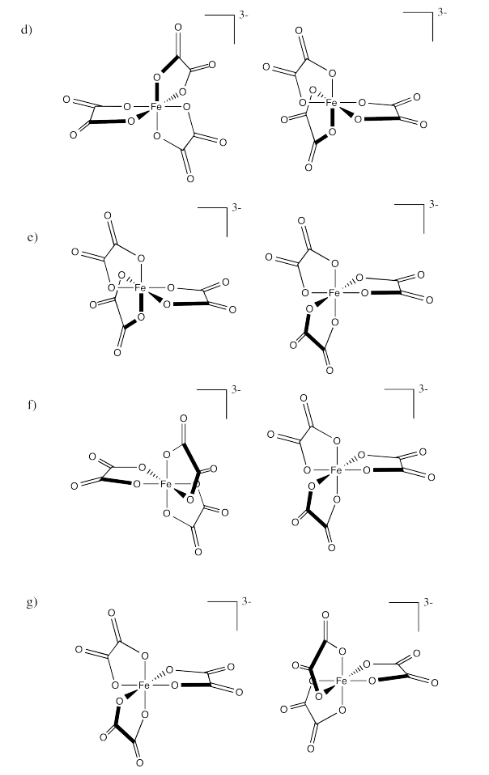
- Answer a:
-
Enantiomers
- Answer b:
-
Enantiomers
- Answer c:
-
Identical
- Answer d:
-
Identical
- Answer e:
-
Enantiomers
- Answer f:
-
Identical
- Answer g:
-
Enantiomers
Exercise \(\PageIndex{2}\)
Indicate whether each of the following compounds is the Δ or Λ isomer and draw its enantiomer.
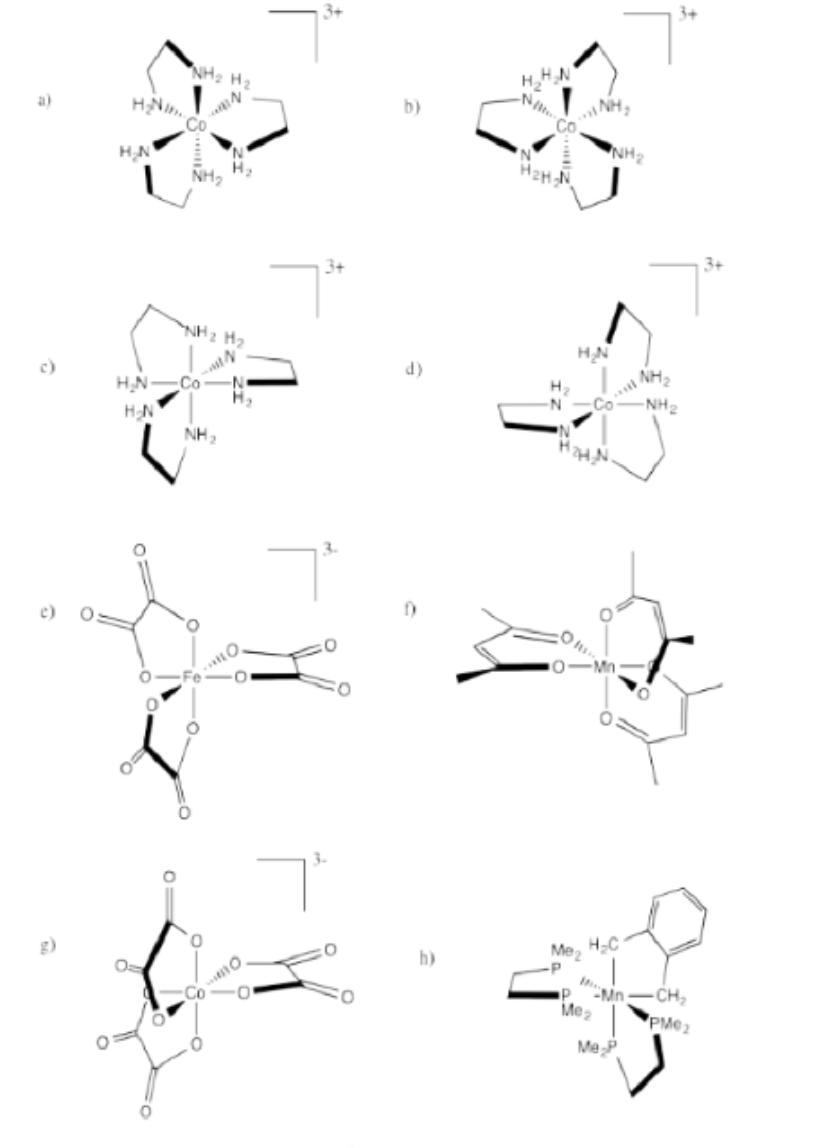
- Answer a:
-
Δ
- Answer b:
-
Λ
- Answer c:
-
Δ
- Answer d:
-
Λ
- Answer e:
-
Δ
- Answer f:
-
Δ
- Answer g:
-
Λ
- Answer h:
-
Λ
Exercise: How many stereoisomers does an octahedral complex have? (contribution from B.J. Johnson)


