2.5: Metals- Solutions to Selected Problems
- Page ID
- 189616
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 2.1.1
The second metal atom is a different size than the principle metal atom. It will not quite fit into the array of atoms. Consequently, the atoms will not be able to slide past each other as easily.
Exercise 2.1.2
\[2Fe: \: (3^{+}) \times 2 = (6^{+}) \nonumber\]
\[3 O: \: (2^{-}) \times 3 = (6^{-}) \nonumber\]
Fe2O3: neutral
Exercise 2.1.3
The longer the box, the longer the possible wavelength.
Exercise 2.2.1
The pattern also repeats diagonally.
Exercise 2.2.2
The squares can form a number of regularly repeating patterns. The rows can exactly repeat (an aaa pattern), or they can be shifted slightly, so that every other row exactly repeats the first row (an ababab pattern). They could even be shifted so that every third row is an exact repeat of the first (abcabcabc).
The pentagons do not form a repeating layer in two dimensions.
Exercise 2.2.3
In the simple square packing, the holes are roughly diamond shaped.
In the hexagonal pattern, the holes are roughly triangular.
Exercise 2.2.6
- Using quarters, the distance is about 5 mm.
- Using quarters, the distance is about 2.5 mm.
A free electron would be closer to the atoms in a hexagonal close packed layer. There would be stronger electron-ion attraction in that case.
Exercise 2.2.7
- Using dimes, the distance is about 3.5 mm.
- Using dimes, the distance is about 1.5 mm.
A free electron would be closer to the atoms if the atoms were smaller. There would be stronger electron-ion attraction in that case.
Exercise 2.2.8
- melting points (and force of attraction between atoms): Fr < Cs < K < Na < Li
- This trend mirrors the sizes of the atoms. Lithium is the smallest and francium the largest. The electron / ion attraction is greatest in Li and weakest in Fr.
Exercise 2.2.9
a) The total area of this square is
\[Area \:= w^{2} \nonumber\]
in which w = width of the unit cell. The width of the unit cell is
\[w = 2r \nonumber\]
in which r = radius of titanium atom.
\[Area \: = 4r^{2} = 4(2.00 \times 10^{-10} m)^{2} = 4(4.00 \times 10^{-20} m^{2}) = 1.60 \times 10^{-19} m^{2} \nonumber\]
b) The total area of this rhombus is
\[ Area \: = s^{2} sin \theta \nonumber\]
in which s = one side of unit cell and θ = an angle of the unit cell (either 60° or 120°). But
\[s = 2r \nonumber\]
in which r = radius of titanium atom.
\[Area \: = (2 \times 2.00 \times 10^{-10} m)^{2} \: sin(60) = 1.60 \times 10^{-19} \: (0.87) m^{2} = 1.39 \times 10^{-19} m^{2} \nonumber\]
Exercise 2.2.10
- \( 4 \times \frac{1}{4} = \: 1 \: atom\)
- \( 2 \times \frac{1}{6} + 2 \times \frac{1}{3} = \frac{2}{6} + \frac{4}{6} = \: 1 \: atom\)
Exercise 2.2.11
The cross-sectional (two dimensional) area of a titanium atom is the area of a circle
\[Area \: = \pi r^{2} \nonumber\]
\[Area \: = 3.1415 \times (2.00 \times 10^{-10} m)^{2} = 3.1415 \times 4.00 \times 10^{-20} m^{2} = 1.257 \times 10^{-19} m^{2} = 1.26 \times 10^{-19} m^{2} \nonumber\]
Exercise 2.2.12
- \(Efficiency \: = \frac{occupied}{total} \times 100 \% = (\frac{1.26 \times 10^{-19} m^{2}}{1.60 \times 10^{-19} m^{2}}) \times 100 \% = 79 \%\)
- \(Efficiency \: = (\frac{occupied}{total}) \times 100 \% = (\frac{1.26 \times 10^{-19} m^{2}}{1.39 \times 10^{-19} m^{2}}) \times 100 \% = 91 \%\)
A greater percentage of space is occupied in hexagonal close packing.
Exercise 2.2.13
- coordination number = 4
- coordination number = 6
Exercise 2.2.14
- Assuming the pattern extends linearly, coordination number = 2. Otherwise, coordination number = 2 for interior atoms and coordination number = 1 for terminal atoms.
- Assuming the pattern extends in two dimensions, coordination number = 3. Otherwise, coordination number = 3 for interior atoms, coordination number = 2 for side edge atoms and coordination number = 1 for corner atoms.
Exercise 2.3.0
- (i) 8; (ii) 6
- (i) 4; (ii) 4
- (i) 5; (ii) 5
- (i) 5; (ii) 6
- (i) 6; (ii) 8
Exercise 2.3.1
- 1/8 atom at each corner
- 8 corners in a cube
- \(8 \times \frac{1}{8} = 1\) atom per simple cube
Exercise 2.3.2
- 1/8 atom at each corner
- 8 corners in a cube
- 1 atom in middle of cube
- \(1 + 8 \times \frac{1}{81 + 8 x 1/8 = 2 atoms per body-centered cube
Exercise 2.3.3
Hexagonal close packed pattern is ABAB.
Exercise 2.3.4
- At both the top and bottom layer, two atoms are 1/3 within the cell and two atoms are 1/6 within the cell.
- That makes \(2 \times (2 \times \frac{1}{3} + 2 \times \frac{1}{6}) = \frac{4}{3} + \frac{4}{6} = \frac{4}{3} + \frac{2}{3} = 1\) atom total in corners
- 1 atom inside the cell.
- 2 atoms total.
Exercise 2.3.5
The pattern in this variation is ABACA.
Exercise 2.3.6
ABCABC.
Exercise 2.3.7
- The rhombus-shaped hexagonal unit cell.
- 4 layers.
Exercise 2.3.8
- 1/8 atom at each corner
- 8 corners in a cube
- 1/2 atom on each face of cube
- \(6 \times \frac{1}{2} + 8 \times \frac{1}{8} = 4\) atoms per face-centered cube
Exercise 2.3.9
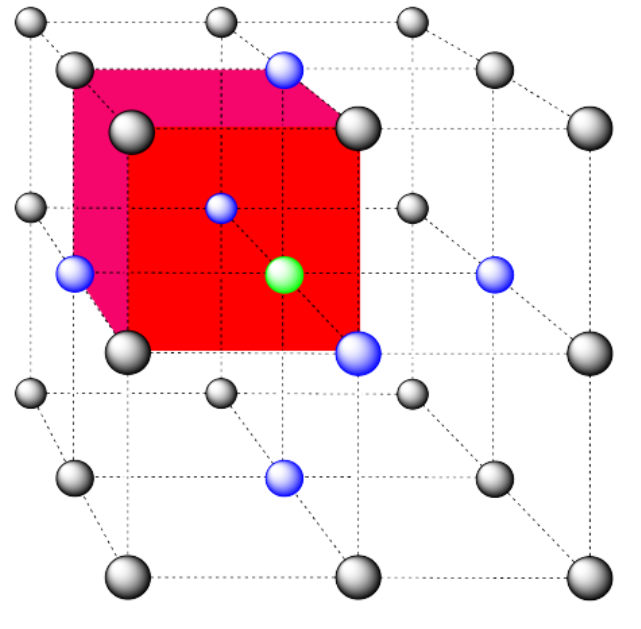
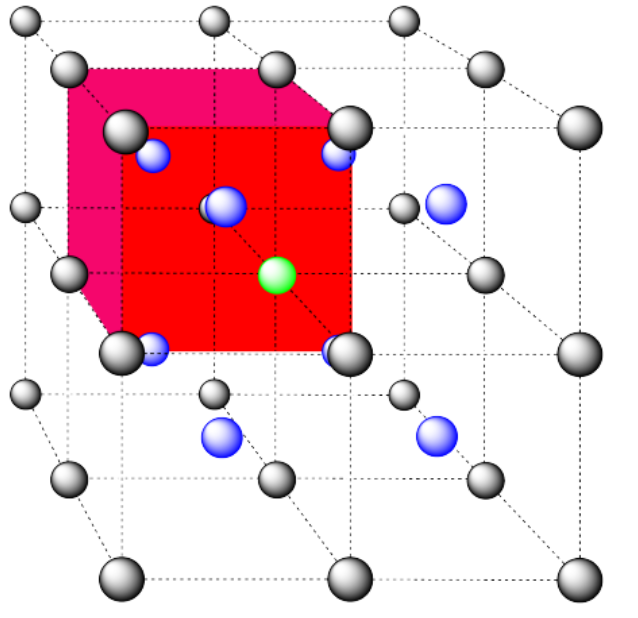
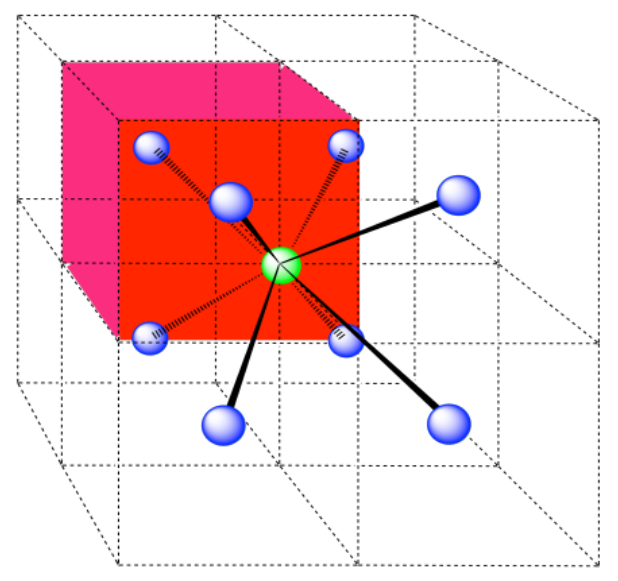
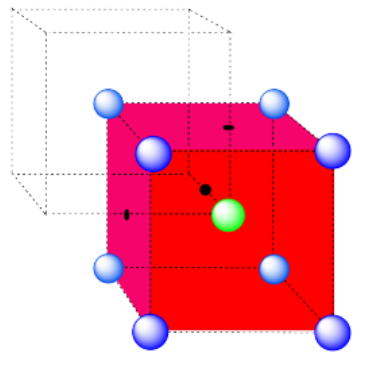
a) coordination number = 6 (3 within the cube, along the three adjacent edges, plus three on adjacent cubes).
In the picture, consider the green atom coordinated by its nearest neighbors, the blue atoms. One unit cell is highlighted in red.
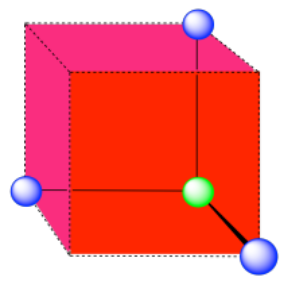
Here is the coordination environment without the surrounding atoms.
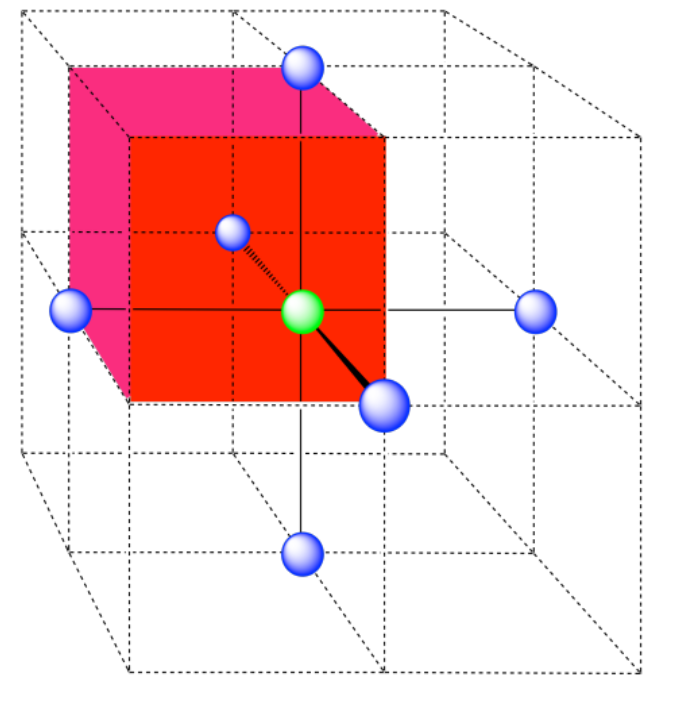
A single unit cell is shown for comparison. The three other nearest atoms are in cells below, behind and to the right of the one shown.
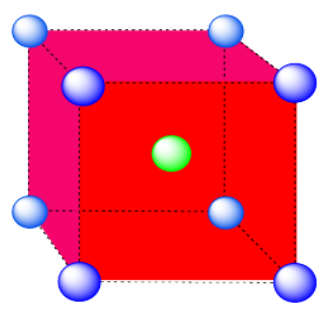
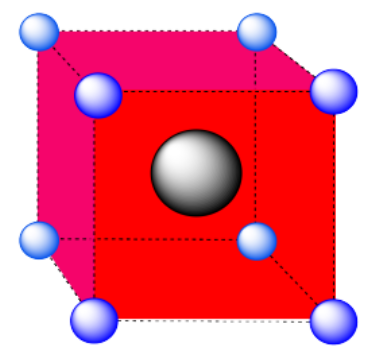
b) coordination number = 8 (corners of the cube).
Here is the coordination environment without the surrounding atoms.
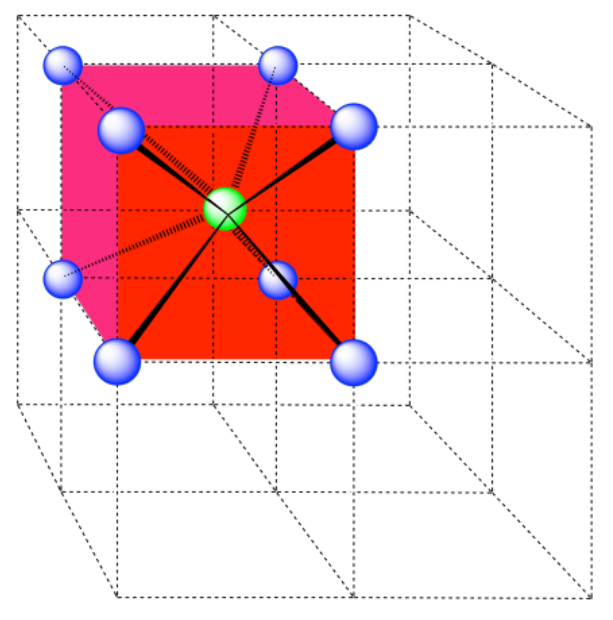
A single unit cell is shown below for simplicity. All of the coordinated atoms are found within the cell.
c) the closest atoms are in the centers of the adjacent cells; the other corners are further away; coordination number = 8.
Here is the coordination environment without the surrounding atoms.
A single unit cell is shown below, for simplicity. Because the atom is in a corner, there are eight other cells arranged around this one: one on the right, two behind, and then four more below.
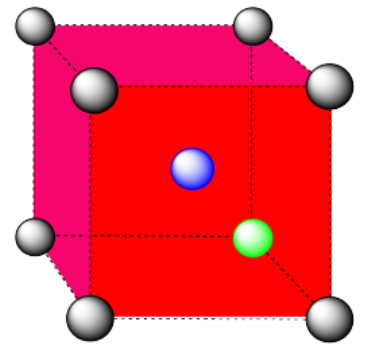
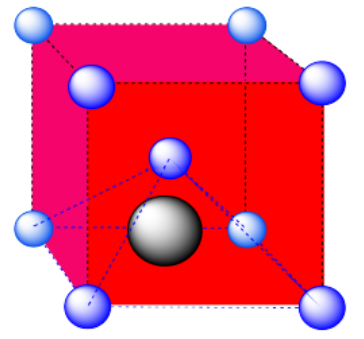
d) The closest atoms are on the faces adjacent to the corner position; these faces are found along three planes, with four faces surrounding the corner on each plane; coordination number = 12.
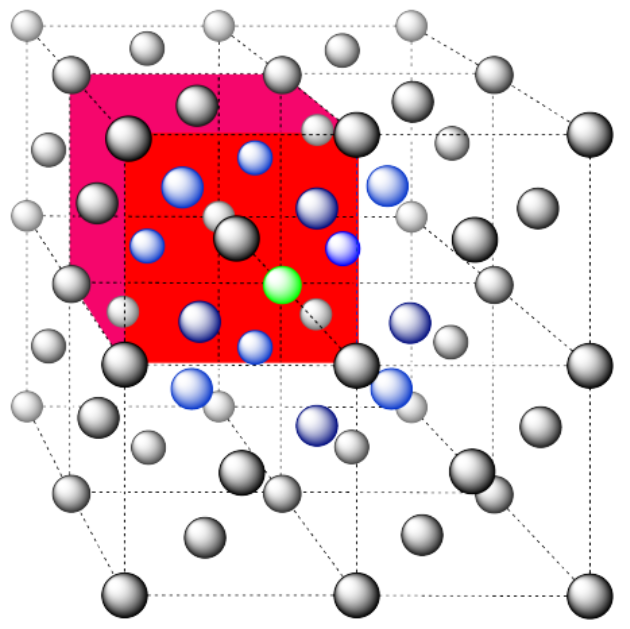
Here is the coordination environment, without the atoms that are further from the green one.
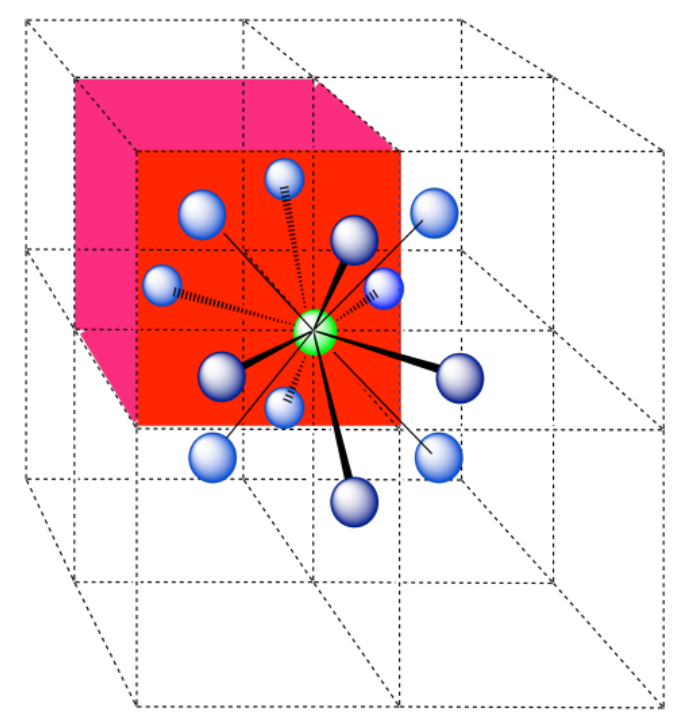
A single unit cell is shown below. Because the atom is in a corner, there are seven other cells arranged around this one: one on the right, two behind, and then four more below.

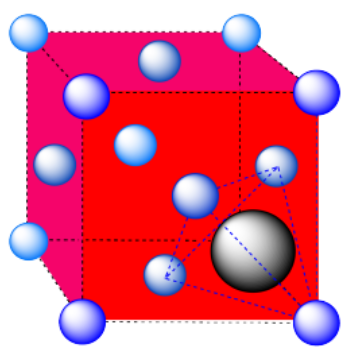
e) The closest atoms are at the corners around the face (4), as well as the atoms in the middle of each adjacent face (8); coordination number = 12.
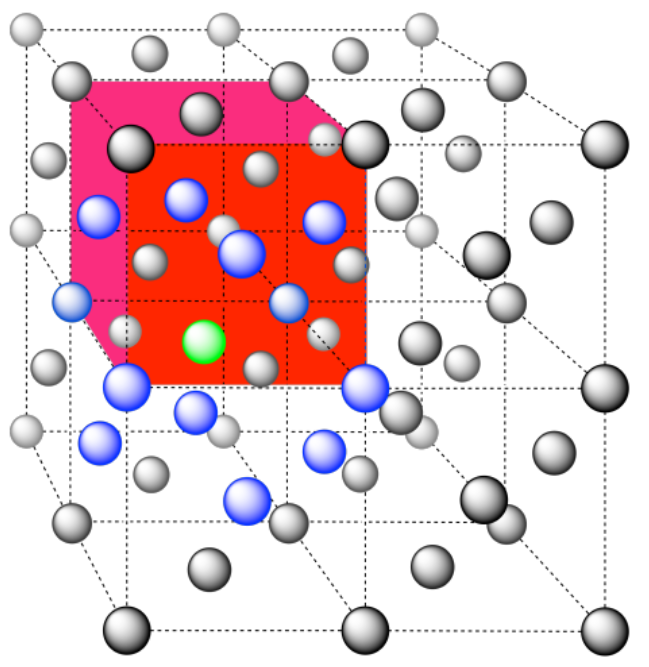
Here is the coordination environment without the other atoms.
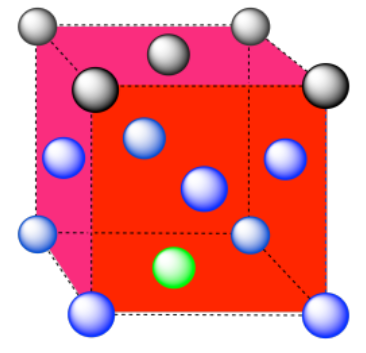
A single unit cell is shown below. There is another cell directly below it.
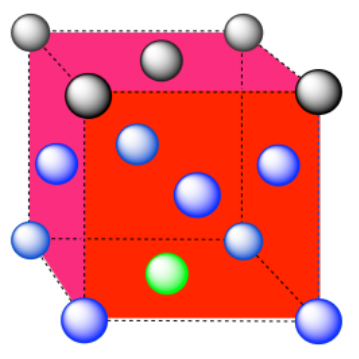
Exercise 2.3.10
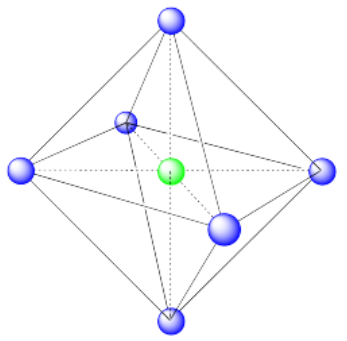
a) Octahedral. An octahedron has six vertices and eight faces.
b) Cubic. A cube has eight vertices and six faces.
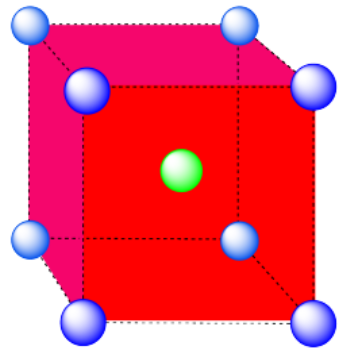
c) This is also a cube, translated from the last one (i.e. the cube is just shifted to a different position in the lattice).
Exercise 2.3.11
a) A cubic hole.
b) A square pyramidal hole. The atom in the hole is above a square of atoms, with an additional atom right above it.
c) An octahedral hole. The atom occupying the hole has been pushed all the way to the face of the cube. It is right in the middle of a square of atoms. One of the vertices is in the center of the next cube.

d) A tetrahedral hole. Note that the layers in the cubic closest-packed system run diagonally through the cubic unit cell. The atom in the hole sits above a trio of atoms on three adjacent faces, and is topped by the atom in the corner of the cube. Because a tetrahedron is so symmetric, the arrangement can be described in a number of other ways, choosing any three surrounding atoms as the base and the fourth atom as the cap of the tetrahedron.
e) An octahedron. Again, the hexagonal layers run diagonally through the unit cell.

Exercise 2.3.16
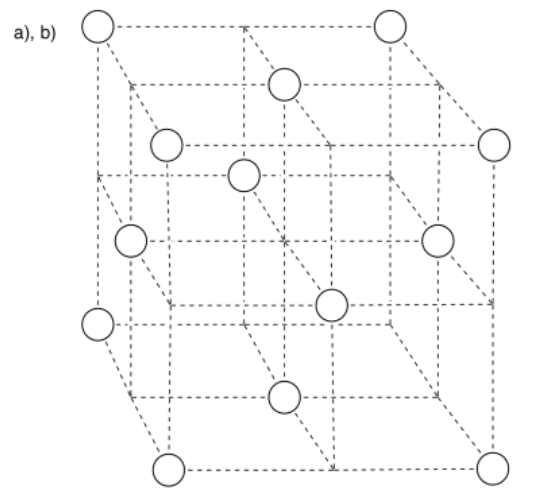
Exercise 2.4.1
c) There are eight atoms in the corner; each is shared by eight neighbouring cubes. There are six atoms on the faces; each is shared by two neighbouring cubes.
\[ \# \: atoms = 8 (\frac{1}{8})+ 6 (\frac{1}{2}) = 1 + 3 = 4 \: atoms \nonumber\]
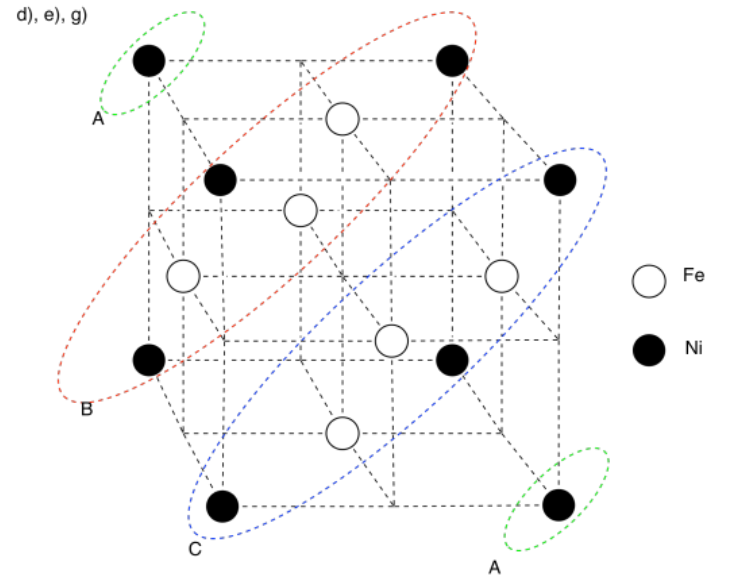
h) Nickel is a little smaller than iron. A row of atoms rolling along in the layer above would fall into the "pothole" caused by the smaller nickel atom and get stuck.


