18.11: Catalysis
- Page ID
- 49622
Altering the mechanism of a reaction so that the activation energy is lower is the second major way to speed up the reaction. A catalyst can do this by participating in the activated complex for the rate-limiting step, even though the catalyst itself is neither a reactant nor a product in the overall stoichiometric equation. A good example of catalysis is provided by the effect of I2 on the rate of isomerization of cis-2-butene. You will recall that the rate law for the catalyzed reaction involves the concentration of I2 raised to the one-half power. This implies that half a molecule of I2 (that is, an I atom) is involved in the activated complex, which probably has the structure
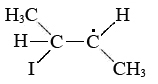
Since there is no double bond between the two central C atoms, one end of the activated complex can readily twist around the other.
The currently accepted mechanism for this catalyzed reaction involves three steps:
\[\frac{1}{2} \ce{I2} \rightleftharpoons \ce{I} \nonumber \]
\[\ce{I + cis-C4H8 -> trans-C4H8 + I} \nonumber \]
\[\ce{I} \rightleftharpoons \ce{ \frac{1}{2} I2} \nonumber \]
The first and last steps have coefficients of one-half associated with I2 because each I2 molecule that dissociates produces two I atoms, only one of which is needed to help a given cis-2-butene molecule to read. Note also that for every I2 molecule which dissociates in the first step of the mechanism, an I2 molecule is eventually regenerated by the last step. As a result, the concentration of I2 after the reaction remains exactly the same as before.
If we consider the energetics of each step in the proposed mechanism, we find that much less than the 262 kJ mol–1 activation energy of the uncatalyzed reaction is required. A complete energy profile for the catalyzed process is compared with that of the uncatalyzed one in Figure 1. The bond enthalpy is 151 kJ mol–1 (from Table 1 in the bond enthalpy section), and so 75.5 kJ mol–1 will be required for formation of the I atom in the first step. An additional increase in energy occurs as the I atom collides with cis-2-butene and bonds with it. Then about 12 kJ mol–1 is required for twisting around the C—C single bond in the activated complex. All told 115 kJ mol–1 is required to go from the initial molecules to the activated complex. When rotation to a trans structure is complete, the I atom dissociates fromtrans-2-buten and eventually reacts with another I atom to form I2. These last two processes involve an overall decrease in energy which is nearly the same as the increase required to achieve the activated complex.
The reduction in activation energy illustrated in Figure \(\PageIndex{1}\) is the chief factor in speeding up the catalyzed reaction.
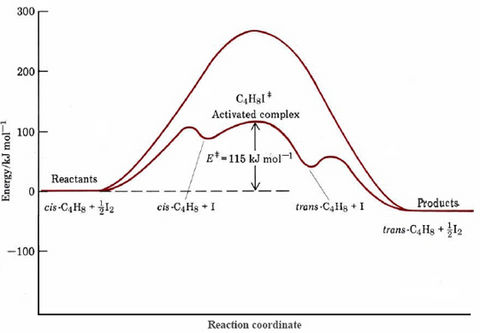
Based on activation energies given, how many times larger would the rate constant be for the catalyzed rather than for the uncatalyzed isomerization of cis-2-butene at a temperature of 500 K?
Solution
The fraction of molecules which have sufficient energy to achieve the activated complex can he calculated using equation 1 from the section on the effect of temperature on catalysis:
\[\text{Fraction (catalyzed)} = 10^{\dfrac{-115 \frac{kJ}{mol}}{(2.303 \times 8.314 \frac{J}{K*mol}*500K)}} = 10^{-12.0} = 1 \times 10^{-12} \nonumber \]
\[\text{Fraction (uncatalyzed)} = 10^{\dfrac{-262 \frac{kJ}{mol}}{(2.303 \times 8.314 \frac{J}{K*mol}*500K)}} = 10^{-27.4} = 4 \times 10^{-28} \nonumber \]
Since the respective rate constants should be proportional to these fractions,
\[\dfrac {k (catalyzed)}{k(uncatalyzed)} = \frac{1*10^{-12}}{4 \times 10^{-28}} = 2.5 \times 10^{15} \nonumber \]
Thus at unit concentrations of cis-2-butene and iodine, the catalyzed reaction will be more than 1015 times faster.
Another example of catalysis is involved in the reaction between H2O2 and the I– ion. In discussing this reaction in example 2 in the rate equation section we noted that it is first order in H2O2 and first order in I– ion between pH = 3 and pH = 5. At lower pH values, however, a different mechanism takes over, and the rate law becomes
\[\text{Rate}= k(c_{H_2O_2})(c_{I^-})(c_{H^+}) \nonumber \]
This indicates that the activated complex contains an additional proton when compared with the uncatalyzed case. This proton apparently adds to the H2O2 molecule, forming H3O2+. Because of the positive charge, less energy increase occurs as an I– ion approaches H3O2+ and the reaction
\[\ce{H3O2+ + I- -> H2O + HOI} \nonumber \]
has a lower activation energy than
\[\ce{H2O2 + I- -> OH- + HOI} \nonumber \]
The latter is the rate-limiting step in the mechanism at higher pH (Eqs. (1a), (1b), and (1c) in the reaction mechanisms section), and so protonating H2O2 results in a faster overall reaction. Measurements over a range of temperatures show that the activation energy is lowered from 56 to 43.6 kJ mol–1 by this change of mechanism.
The peroxide-iodide reaction is one example of a great many acid-catalyzed reactions. In most of these the hydrogen ion concentration appears in the rate law, indicating that the activated complex contains an extra proton. The positive charge of this proton allows negative ions to combine more readily with the protonated species. The proton may also shift electron density toward itself and away from some other site in the protonated molecule, allowing a negative species to bond to that site more readily. The net result is a lower activation energy and a more rapid reaction. The preceding examples are illustrative of the three main features of catalysis:
- The catalyst allows the reaction to proceed via an alternative mechanism.
- The catalyst is directly involved in this mechanism, but for every step in which a catalyst molecule is a reactant, there is another step where the catalyst appears as a product. Thus there is no net consumption of the catalyst.
- The catalyzed mechanism results in a faster reaction, usually because the overall activation energy is lowered.


