18.5: Unimolecular Processes
- Page ID
- 49589
A reaction is said to be unimolecular if, on the microscopic level, rearrangement of the structure of a single molecule produces the appropriate product molecules. An example of a unimolecular process is conversion of cis-2-butene to trans-2-butene (in the absence of any catalyst):
All that is required for this reaction to occur is a twist or rotation around the double bond, interchanging the methyl group with the hydrogen atom on the right-hand side. Only one cis-2-butene molecule need be involved as a reactant in this process.
Rotating part of a molecule about a double bond is not easy, however, -because it involves a distortion of the electron clouds forming the double bond. This barrier to rotation was described in orbital descriptions of multiple bonds. A considerable increase in energy is required to twist one end of cis-2-butene around the other. This is shown in Figure 1, where the energy has been plotted as a function of the angle of rotation. The maximum energy is reached when one end of the molecule has been rotated by 90° with respect to the other.
This conformation is 262 kJ mol–1 higher than the energy of the original planar molecule. From this maximum it is downhill energetically on either side; so if the molecule has twisted this far, it should keep on twisting, eventually becoming trans-2-butene when the angle of rotation reaches 180°. Trans-2-butene is slightly lower in energy than cis-2-butene, as indicated the enthalpy change of – 4 kJ mol–1 for the overall reaction.
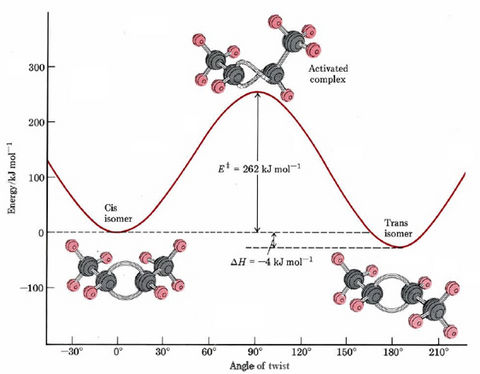
Figure \(\PageIndex{1}\) shows that the barrier to rotation around a double bond is an energy barrier. At least 262 kJ mol–1 must be supplied to transform cis-2-butene into trans-2-butene by a rotation such as we have described. The minimum quantity of energy required to surmount an energy barrier during a chemical reaction is called the activation energy, and the molecular species at the top of the barrier is called the activated complex or the transition state. Quantities associated with this activated complex are usually denoted by a double dagger (‡). For example, the activation energy is given the symbol E‡.
In the sample of gaseous cis-2-butene at room temperature, only a tiny fraction of molecules have enough energy to surmount the activation-energy barrier. (Recall from figure 2 in the section on molecular speed distribution in gases that only a very small fraction of all gas molecules are traveling at very high speeds and hence have large kinetic energies. The same applies to the energy a molecule has because it is vibrating or rotating.) Not only do few molecules have enough energy to overcome the activation-energy barrier, but fewer still have that energy concentrated so that it can cause the atomic movements needed for the reaction to occur. In the case of cis-2-butene for example, very few of the high-energy molecules have their energy distributed so that most of it is causing a twist around the double bond. Thus over a given period of time only a very small fraction of the cis-2-butene molecules will be converted to trans-2-butene.
Now suppose that we double the concentration of a sample of cis-2-butene. This means that there will be twice as many molecules in each cubic decimeter. At a given temperature the fraction of the molecules which can react during a given time interval will be the same, but with twice as many molecules there will be twice as many conversions to trans-2-butene. Therefore in a period of 1 s the change in the amount of substance per unit volume will be twice as great, and this means that the reaction rate is twice as great.
What we have just said applies to any unimolecular process. The reaction rate must always be directly proportional to the concentration of the reacting species. That is, for a general unimolecular process, A → products, the rate equation must be first order in A:
\[Rate = kc_A \nonumber \]


