9.4: Measurement of Pressure
- Page ID
- 49360
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The pressure of the atmosphere is exerted in all directions, not just downward, at any given altitude. You can show this with a simple party trick that allows you to invert a cup of water without spilling a drop.
The video above certainly goes a long way towards showing that air exerts pressure in all directions, but how do we go about measuring that pressure? Below you see a barometer, which is a device for measuring pressure invented a long time ago and is still used today. To find out how it works, read on.
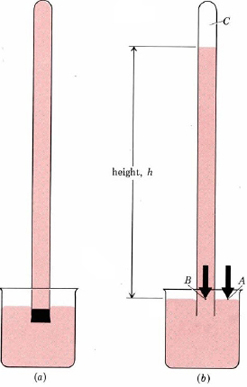
Barometers measure pressure in a rather indirect way, using liquid displacement to define how how much pressure is applied. An inverted tube (see above) is placed into a beaker full of a liquid (often mercury or water). The pressure of the air presses down on the liquid in the beaker, causing it to rise into the tube. The amount of liquid that rises into the tube can be measured (usually in terms of height) and compared, giving us a comparable and repeatable measurement.
To summarize, the maximum height of liquid which can be supported by atmospheric pressure provides a measure of pressure. It turns out that a column of water about 10 m (more than 30 ft) high can be held up by earth's atmosphere. This would be an inconvenient height to measure in the laboratory, and so a much denser liquid, mercury, is used instead. The mercury barometer, a device for measuring atmospheric pressure, is shown in Figure \(\PageIndex{1}\).
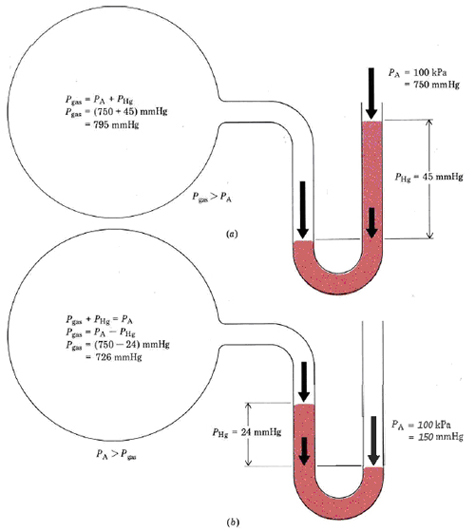
Another tool of measurement is the manometer, pictured below. A manometer has a bulb (pictured below as the giant circle) with a known pressure. The tube section connected to the ball is filled with a liquid, in this case mercury. The end of the tube is open to the atmosphere, which exerts a pressure on the mercury. The pressure inside of the bulb exerts a pressure from the other side.
If the atmospheric pressure is greater than the internal pressure, the manometer will look like the second image. If the atmospheric pressure is less than the internal pressure, then the manometer will look like the first image. If the pressures are the same, the levels will be equal on each side. The difference in height between the two sides of the two can be quantified, providing a measurement of pressure.
Although the Pascal is the accepted SI unit of pressure, it is not yet in general use in the United States. Therefore, one must also be familiar with the atmosphere. The atmosphere is also convenient because 1.000 atm is nearly the same as the atmospheric pressure each of us experiences every day of our lives. This gives a concrete reference with which other pressures can be compared. For these reasons we will usually employ the atmosphere as the unit of pressure for the remainder of this chapter. Nevertheless, there are a number of cases where using the Pascal gives a significant insight into gas behavior. In such cases we shall use the newer internationally recognized unit.
A barometer is constructed as shown in Figure 1. The cross-sectional area of the tube is 1.000 cm², and the height of the mercury column is 760.0 mm. Calculate the atmospheric pressure.
Solution First calculate the volume of mercury above point B. Use the density of mercury to obtain the mass, and from this, calculate force and pressure as in Example 1 from "Pressure."
\(V = 1.000 \text{ cm}^{2} \times 760.0 \text{ mm} = 1000 \text{ cm} \times 760.0 \text{ mm} \times 1 \text{ cm} \times (10 \text{ mm})^{-1} = 76.00 \text{ cm}^{-3}\) \( m_\text{Hg} = 76.00 \text{ cm}^{3} \times 13.595 \text{ g}\text{ cm}^{-3} = 1033.2 \text{ g} = 1.0332 \text{ kg} \)\(F = ma = 1.0332 \text{ kg} \times 9.807 \text{ m}\text{ s}^{-2} = 10.133 \text{ kg m}\text{ s}^{-2}= 10.133 \text{ N}\)
\(P = \frac{F}{A} = \frac{10.133 \text{ N}}{1 \text{ cm}^{2}} = \frac{10.133 \text{ N}}{1 \text{ cm}^{2}} \times \big( \frac{100 \text{ cm}}{\text{m}}\big) ^{2} = 10.133 \times 10^{4} \text{ N} \text{ m}^{-2} = 101.33 \text{ kPa}\)
The preceding example shows that a mercury column 760.0 mm high and 1.000 cm2 in area produces a pressure of 101.33 kPa (1 atm). It can also be shown that only the height of the mercury column affects its pressure. For a larger cross section there is a greater mass of mercury and therefore a greater force, but this is exerted over a greater area, leaving force per unit area unchanged. For this reason it is convenient to measure pressures of gases in terms of the height of a mercury column that can be supported. That is, we might report the atmospheric pressure in Example 1 as 760 mmHg instead of 101.3 kPa or 1.000 atm. It is useful to remember that \(760 \text{ mmHg} = 1.000 \text{ atm} = 101.3 \text{ kPa}\) The pressure of a gas in a container is often measured relative to atmospheric pressure using a manometer. This is a U-shaped tube containing mercury and connecting the container to the air (Figure 2).A mercury manometer is used to measure the pressure of a gas in a flask. As shown in Figure 2b, the level of mercury is higher in the arm connected to the flask, but the difference in levels is 43 mm. Barometric pressure is 737 mmHg. Calculate the pressure in the container (a) in millimeters of mercury; (b) in kilopascals; and (c) in atmospheres.
Solution
a) \( P_{gas} + P_{Hg} = P_{A} \)\( P_{gas} = P_{A} - P_{Hg} \)
\(P_{gas} = 737 \text{ mmHg} - 43 \text{ mmHg} = 694 \text{ mmHg}\)
b) \(P_{gas}=\text{694 mmHg }\times \text{ }\frac{\text{101}\text{.3 kPa}}{\text{760 mmHg}}=\text{92}\text{.5 kPa}\) c) \(P_{gas}=\text{694 mmHg }\times \text{ }\frac{\text{1 atm}}{\text{760 mmHg}}=\text{0}\text{.913 atm}\)Note that essentially the same procedure suffices to convert from millimeters of mercury to either kilopascals or atmospheres. Laboratory measurements are usually made in millimeters of mercury, but further calculations almost invariably are more convenient if kilopascals or atmospheres are used.


