3.2.3: Everyday Life- Why Fats Don't Add Up on Food Nutrition Labels
- Page ID
- 50015
Equations and Mass Relationships in Everyday Life
If you're observant and pay attention to nutrition labels on foods, you may have noticed labels like the one here, where the fats don't seem to add up.
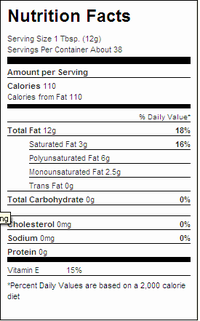
If one 12 g serving of Crisco® contains 3 g of saturated fat, 0g of trans fat, 6 g of polyunsaturated fat, and 2.5 g of monounsaturated fat[1] what happened to the missing 0.5 g of fat? 3 g + 0 g + 6 g + 2.5 g = 11.5 g!
In many cases there's a bigger disparity than this. The fats don't add up[2] because the weight of glycerol is not included in the separately listed components. Trans fatty acids are now recognized as a major dietary risk factor for cardiovascular diseases, and the US FDA has revised food labeling requirements to include trans fats.[3]
Are companies pulling the wool over our eyes? In order to understand what's going on, we need to look into the nature of vegetable fats and oils, which are triglycerides.
Triglycerides
Vegetable fats and oils are all triglycerides, which contain a glycerol (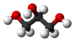 ) three carbon "backbone" with 3 long chain "fatty acids" attached through ester linkages, as in the figure below. The actual shape is shown in the Jmol model, which can be rotated with the mouse. Triglycerides are called "fats" when they're solids or semisolids, and "oils" when they're liquids.
) three carbon "backbone" with 3 long chain "fatty acids" attached through ester linkages, as in the figure below. The actual shape is shown in the Jmol model, which can be rotated with the mouse. Triglycerides are called "fats" when they're solids or semisolids, and "oils" when they're liquids.
|
A triglyceride, overall unsaturated, with the glycerol "backbone" on the left, and saturated palmitic acid, monounsaturated oleic acid, and polyunsaturated alpha-linolenic acid. The shape of the acids is not accurately represented.
|
The long chain fatty acids may be saturated with hydrogen atoms, in which case they have all single bonds like the top fatty acid in the Figure (which is palmitic acid). If they have fewer hydrogen atoms, they are unsaturated and have double bonds like the middle fatty acid in the Figure (which is oleic acid). The bottom fatty acid is polyunsaturated, with multiple double bonds (it is linolenic acid). Various cooking oils have |known concentrations of saturated and unsaturated fatty acids.
As of 2010, Crisco consists of a blend of soybean oil, fully hydrogenated cottonseed oil, and partially hydrogenated soybean and cottonseed oils. Each of these oils is a complex mixture of triglycerides, all with different fatty acid substituents. (We've discussed the benefits and drawbacks of saturated and unsaturated oils elsewhere).
A triglyceride would be called "unsaturated" if it contained just 1 unsaturated fatty acid (and 2 unsaturated), so how can the actual amount of saturated and unsaturated fatty acids be reliably reported? The tryglycerides have to be decomposed into their component fatty acids, and the total amount of each kind (saturated, monounsaturated, and polyunsaturated) reported separately. But this leaves out the glycerol that results from the decomposition, as shown in the equation below for the triglyceride containing 2 palmitic acid (P = C16H32O2) and 1 linolenic acid (L = C18H30O2) substituents. The triglyceride can be abbreviated "GPPL" for glycerol (G) with 2 palmitic acid and 1 linolenic acid (L) substituents:
\[\ce{(C16H32O2)}\textbf{CH}_\textbf{2}\textbf{CH} \ce{(C16H32O2)}\textbf{CH}_\textbf{2}\ce{-(C18H30O2) + 3 H2O} \xrightarrow{\ce{NaOH}} \ce{1 C3H6O3 + 2 C16H32O2 + 1 C18H30O2} \nonumber \]
-
-
-
-
- GPPL + 3 H2O Glycerol + 2 P + 1 L (1)
-
-
-
This is called a "hydrolysis" reaction, because water causes the decomposition. Sodium hydroxide (NaOH) written above the arrow indicates that NaOH is a catalyst, and isn't consumed or integrated into the products of the chemical reaction.
This balanced chemical equation can tell us where the missing mass from the nutrition label has gone.
The equation not only tells how many molecules of each kind are involved in a reaction, it also indicates the amount of each substance that is involved, so it will allow us to find out how much water is consumed and how much glycerol is produced, and those will explain the "missing" masses on the nutrition label.
The equation says that 1 GPPL molecules can react with 3 H2O molecules to give 1 G molecule, 2 P molecules and 1 L molecule. It also says that 1 mol GPPL would react with 3 mol H2O yielding 1 mol G, 2 mol P, and 1 mol L.
The balanced equation does more than this, though. It also tells us that 2 × 1 = 2 mol GPPL will react with 2 × 3 = 6 mol H2O, to form 2 × 1 = 2 mol G, and that ½ × 1 = 0.5 mol GPPL requires only ½ × 3 = 1.5 mol H2O. In other words, the equation indicates that exactly 3 mol H2O must react for every 1 mol GPPL consumed, and for every 1 mol GPPL is consumed, 1 mol G, 2 mol P, and 1 mol L will be produced. For the purpose of calculating how much H2O is require to react with a certain amount of GPPL, the significant information contained in Eq. (1) is the ratio
\[\dfrac {\text {3 mol H}_{\text{2}}{\text{O}}} {\text {1 mol GPPL}} \nonumber \]
We shall call such a ratio derived from a balanced chemical equation a stoichiometric ratio and give it the symbol S. Thus, for Eq. (1), \(\text{S}\left( \frac{\text{H}_{\text{2}}\text{O}}{\text{GPPL}} \right)~=~\frac{\text{3 mol H}_{\text{2}}\text{O}}{\text{1 mol GPPL}\text{)}}\)
The word stoichiometric comes from the Greek words stoicheion, “element,“ and metron, “measure.“ Hence the stoichiometric ratio measures one element (or compound) against another.
Derive all possible stoichiometric ratios from Eq. (1)
Solution
Any ratio of amounts of substance given by coefficients in the equation may be used:
\[\text{S}\left( \frac{\text{GPPL}}{\text{G}} \right)=\frac{\text{1 mol GPPL}}{\text{1 mol G}}\]
\[\text{S}\left( \frac{\text{L}}{\text{P}} \right)=\frac{\text{1 mol L}}{\text{2 mol P}}\]
\[\text{S}\left( \frac{\text{GPPL}}{\text{P}} \right)=\frac{\text{1 mol GPPL}}{\text{2 mol P}}\]
\[\text{S}\left( \frac{\text{L}}{\text{H}_{\text{2}}\text{O}} \right)=\frac{\text{1 mol L}}{\text{3 mol H}_{\text{2}}\text{O}}\]
\[\text{S}\left( \frac{\text{P}}{\text{H}_{\text{2}}\text{O}} \right)=\frac{\text{2 mol P}}{\text{3 mol H}_{\text{2}}\text{O}}\]
\[\text{S}\left( \frac{\text{G}}{\text{H}_{\text{2}}\text{O}} \right)=\frac{\text{1 mol G}}{\text{3 mol H}_{\text{2}}\text{O}}\]
When any chemical reaction occurs, the amounts of substances consumed or produced are related by the appropriate stoichiometric ratios. Using Eq. (1) as an example, this means that the ratio of the amount of H2O consumed to the amount of GPPL consumed must be the stoichiometric ratio S(H2O/GPPL):
\(\frac{n_{\text{H}_{\text{2}}\text{O}\text{ consumed}}}{n_{\text{GPPL}\text{ consumed}}}\)\(=\text{S}\left( \frac{\text{H}_{\text{2}}\text{O}}{\text{GPPL}} \right)=\frac{\text{3 mol H}_{\text{2}}\text{O}}{\text{1 mol GPPL}}\) Similarly, the ratio of the amount of G produced to the amount of GPPL consumed must be
S(G/GPPL):
\[\frac{n_{\text{G produced}}}{n_{\text{GPPL}\text{ consumed}}}~=~\text{S}\left( \frac{\text{G}}{\text{GPPL}} \right)=\frac{\text{1 mol G}}{\text{1 mol GPPL}}\]
In general we can say that
\[\text{Stoichiometric ratio }\left( \frac{\text{X}}{\text{Y}} \right)=\frac{\text{amount of X consumed or produced}}{\text{amount of Y consumed or produced}}\text{ (3}\text{a)}\]
or, in symbols,
\[\text{S}\left( \frac{\text{X}}{\text{Y}} \right)=\frac{n_{\text{X consumed or produced}}}{n_{\text{Y consumed or produced}}}\text{ (3}\text{b)}\]
Note that in the word Eq. (3a) and the symbolic Eq. (3b), X and Y may represent any reactant or any product in the balanced chemical equation from which the stoichiometric ratio was derived. No matter how much of each reactant we have, the amounts of reactants consumed and the amounts of products produced will be in appropriate stoichiometric ratios.
Find the amount of glycerol produced when 3.68 mol H2O is consumed according to Eq. (1).
(C16H32O2)CH2CH(C16H32O2)CH2-(C18H30O2) + 3 H2O \(\xrightarrow{\text{NaOH}}\)1 C3H6O3 + 2 C16H32O2 + 1 C18H30O2
-
-
-
-
- GPPL + 3 H2O \(\xrightarrow{\text{NaOH}}\) Glycerol + 2 P + 1 L (1)
-
-
-
Solution
The amount of glycerol produced must be in the stoichiometric ratio S(G/H2O)to the amount of water consumed:
\[\text{S}\left( \frac{\text{G}}{\text{H}_{\text{2}}\text{O}} \right)=\frac{n_{\text{G produced}}}{n_{\text{H}_{\text{2}}\text{O consumed}}}\]
Multiplying both sides nH2O consumed, by we have
\[n_{\text{G}\text{O produced}}=n_{\text{H}_{\text{2}}\text{O}\text{ consumed}}\times \text{S}\left( \frac{\text{G}}{\text{H}_{\text{2}}\text{O}} \right)=\text{3}\text{.68 mol H}_{\text{2}}\text{O}\times \frac{\text{1 mol G}}{\text{3 mol H}_{\text{2}}\text{O}}=\text{1}\text{0.23 mol H}\]
This is a typical illustration of the use of a stoichiometric ratio as a conversion factor. Example 2 is analogous to Examples 1 and 2 from Conversion Factors and Functions, where density was employed as a conversion factor between mass and volume. Example 2 is also analogous to Examples 2.4 and 2.6, in which the Avogadro constant and molar mass were used as conversion factors. As in these previous cases, there is no need to memorize or do algebraic manipulations with Eq. (3) when using the stoichiometric ratio. Simply remember that the coefficients in a balanced chemical equation give stoichiometric ratios, and that the proper choice results in cancellation of units. In road-map form \(\text{amount of X consumed or produced}\overset{\begin{smallmatrix} \text{stoichiometric} \\ \text{ ratio X/Y} \end{smallmatrix}}{\longleftrightarrow}\text{amount of Y consumed or produced}\) or symbolically. \(n_{\text{X consumed or produced}}\text{ }\overset{S\text{(X/Y)}}{\longleftrightarrow}\text{ }n_{\text{Y consumed or produced}}\)
When using stoichiometric ratios, be sure you always indicate moles of what. You can only cancel moles of the same substance. In other words, 1 mol NH3 cancels 1 mol NH3 but does not cancel 1 mol H2O
The next example shows that stoichiometric ratios are also useful in problems involving the mass of a reactant or product.
- Calculate the mass of glycerol (G) produced when 3.84 mol GPPL is reacted with adequate H2O according to Equation (1).
- Show that a nutritional label for this fat would have trans, unsaturated, and polyunsaturated fats that don't add up to the total fat.
Solution
The problem asks that we calculate the mass of glycerol produced. As we learned in Example 2 of The Molar Mass, the molar mass can be used to convert from the amount of glycerol to the mass of glycerol. Therefore this problem in effect is asking that we calculate the amount of glycerol produced from the amount of GPPL consumed. This is the same problem as in Example 2. It requires the stoichiometric ratio
\[\text{S}\left( \frac{\text{G}}{\text{GPPL}} \right)=\frac{\text{1 mol G}}{\text{1 mol GPPL}}\]
The amount glycerol, G, produced is then
\[n_{\text{G produced}}=n_{\text{GPPL consumed}}\text{ }\!\!\times\!\!\text{ conversion factor}=\text{3}\text{.84 mol GPPL}\times \frac{\text{1 mol G}}{\text{1 mol GPPL}}=\text{3}\text{.84 mol G}\]
The mass of glycerol, (G = C3H6O3) is \(\text{m}_{\text{G}}~=~\text{3}\text{.84 mol G}\times \frac{\text{92}\text{.1 g G}}{\text{1 mol G}}=\text{354 g G}\) With practice this kind of problem can be solved in one step by concentrating on the units. The appropriate stoichiometric ratio will convert moles of O2 to moles of SO2 and the molar mass will convert moles of SO2 to grams of SO2. A schematic road map for the one-step calculation can be written as \(n_{\text{G}} ~ \xrightarrow{S\text{(G}\text{/GPPL}\text{)}}~ n_{\text{G}}~\xrightarrow{M_{\text{G}}} ~ m_{\text{G}}\) Thus \(\text{m}_{\text{G}}=\text{3}\text{.84 mol GPPL}\times ~ \frac{\text{1 mol G}}{\text{1 mol GPPL}} ~ \times ~ \frac{\text{92}\text{.1 g}}{\text{1 mol G}}=\text{354 g}\) These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. You may verify the additional calculations.
| C16H32O2)CH2CH(C16H32O2)CH2-(C18H30O2) GPPL |
+ 3 H2O | → C3H6O3 G |
+ 2 C16H32O2 P |
+ 1 C18H30O2 L |
|
|---|---|---|---|---|---|
| m (g) | 3185 | 208 | 354 | 1969 | 1069 |
| M (g/mol) | 829.3 | 18.02 | 92.1 | 256.4 | 278.4 |
| n (mol) | 3.84 | 11.52 | 3.84 | 7.68 | 3.84 |
b. When we calculate the masses of all reactants and products, we get the results shown in the table. In this case, the total mass of fat is 3185 g. It is a mixed saturated (palmitic acid) and polyunsaturated (linolenic acid) fat, that is degraded to 1969 g of saturated fat and 1069 g of polyunsaturated fat. We assume that no trans fat was produced, and no monounsaturated fatty acids are present. So the label would have numbers proportional to:
| Total Fat | 3185 |
| Saturated Fat | 1969 |
| Trans Fat | 0 |
| Unsaturated Fat | 0 |
| Polyunsaturated Fat | 1069 |
The components add up to 3038 g, which is less than the total fat because the mass of glycerol (354 g) and water (207.6) are not accounted for.
Show that the calculation of the mass of water required to react with 3.68 mol of GPPL in the example above is correct.
Solution
Symbolically
\[n_{\text{GPPL}} ~ \xrightarrow{S\text{(H}_{\text{2}}\text{O}\text{/GPPL}\text{)}} ~ n_{\text{H}_{\text{2}}\text{O}}~\xrightarrow{M_{\text{H}_{\text{2}}\text{O}}} ~ m_{\text{H}_{\text{2}}\text{O}}\]
\[3.84 \text{mol GPPL}~\times~\frac{\text{3 mol H}_{\text{2}}\text{O}}{\text{1 mol GPPL}} ~ \times ~ \frac{\text{18}\text{.02 g}}{\text{1 mol H}_{\text{2}}\text{O}}=\text{208 g }\]
References
- www.crisco.com/Products/Produ...=17&prodID=803
- Wolke, R. L. "What Einstein Told His Cook", W.W. Norton & Co., NY 2002, p. 72
- Template:Cite journal


