17.4: Polymerization Ratchet and Translocation Ratchet

Polymerization and translocation ratchets refer to processes that result in directional displacements of a polymer or oligomer chain rather than a specific protein. The models for these ratchets also involve rectified Brownian motion, in which a binding unit is added to a diffusing chain to bias the diffusive motion in a desired direction. Once the displacement reaches a certain diffusion length, a monomer or binding protein can add to the chain, locking in the forward diffusion of the chain. In this case, it is the binding or attachment of protein units that consumes energy, typically in the form of ATP or GTP hydrolysis.

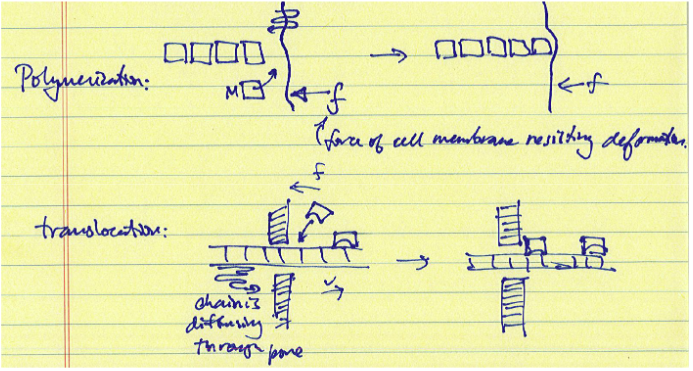
Translocation Ratchet¹

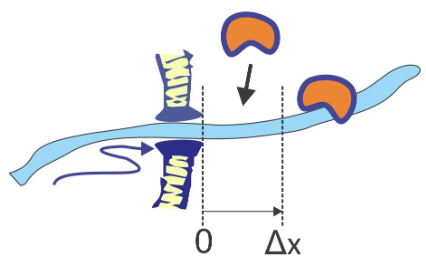Protein translocation across cell membranes is a ubiquitous process for transporting polypeptide chains across bacterial and organelle membranes through channels with the help of chaperone proteins on the inner side of the membrane. The translocation ratchet refers to a model in which the transport of the chain occurs through Brownian motion which is rectified by the binding of proteins to the chain on one side of the pore as it is displaced. Once the chain diffuses through the pore for a distance Δx, a protein can bind to the chain, stopping backward diffusion. At each step, energy is required to drive the binding of the chaperone protein.

The translocation ratchet refers to a continuum model for the diffusion of the chain. It is possible to map this diffusion problem onto a Smoluchowski equation, but it would be hard to solve for the probability density. It is easier if we are just interested in describing the average velocity of the chain under steady state conditions, we can solve for the steady-state chain flux across the pore:

\[J(x) = -D \left( \dfrac{\partial P}{\partial x} + \dfrac{f}{k_BT}P \right) \]

where f is the force acting against the chain displacement. Steady state behavior corresponds to \( \partial P/\partial t =0 \) , so from the continuity equation

\[ \dfrac{\partial P}{\partial t} = -\dfrac{\partial J}{\partial x} \nonumber \]

we know that \(\partial J/\partial x = 0 \). Therefore J is a constant. To find P, we want to solve

\[ \dfrac{\partial P}{\partial x} + \dfrac{f}{k_BT}P+\dfrac{J}{D} = 0 \nonumber \]

for which the general solution is \(P=A_1e^{-fx/k_BT}+A_2\). We find the integration constants using the boundary condition \(P(\Delta x,t )=0 \), which reflects that a protein will immediately and irreversibly bind once the diffusing chain reaches an extension \(\Delta x\). (No back-stepping is allowed.) And we use the conservation statement:

\[ \int_0^{\Delta x} dx P(x) = 1 \nonumber \]

which says that a protein must be bound within the interval 0 to Δx. The steady-state probability distribution with these two boundary conditions is

\[ P(x) = \dfrac{ \underset{ \sim }{f} \left[ \exp \left( \underset{ \sim }{f} (1-x/\Delta x) \right) -1 \right] }{\Delta x\left( 1+ \underset{ \sim }{f} - e^{ \underset{ \sim }{f} } \right) } \]

\[ \underset{ \sim }{f} = \dfrac{f \Delta x}{k_BT} \nonumber \]

\( \underset{\sim}{f}\) is a dimensionless constant that expresses the load force in units of k_BT opposing ratchet displacement by Δx.

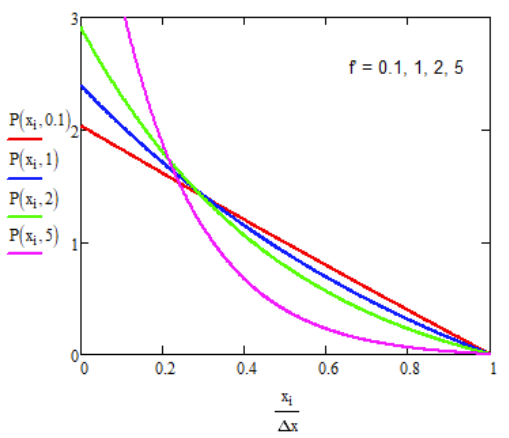
Substituting eq. (17.4.2) into eq. (17.4.1) allows us to solve for J.

\[J(x) =\dfrac{-D\underset{ \sim }{f}^2 }{\Delta x^2\left( 1+ \underset{ \sim }{f}-e^{\underset{ \sim }{f}} \right) } \left( 1-2\exp \left[ \underset{ \sim }{f} \left( \dfrac{x}{\Delta x} -1 \right) \right] \right) \nonumber \]

Now, the average velocity can be determined from \(\langle \nu \rangle = J\Delta x \). Evaluating the flux at x = Δx:

\[ \langle \nu \rangle =\dfrac{2D}{\Delta x} \left[ \dfrac{\underset{ \sim }{f}^2/2}{e^{\underset{ \sim }{f}}-\underset{ \sim }{f}-1} \right] \nonumber \]

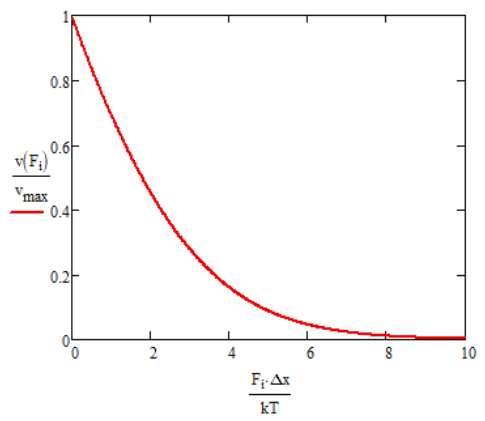
Now look at low force limit \(f \rightarrow 0 \). Expand \(e^{\underset{ \sim }{f}}=1+\underset{ \sim }{f}+\underset{ \sim }{f}^2/2 \):

\[ \langle \nu \rangle \rightarrow \dfrac{2D}{\Delta x} = v_{max} \nonumber \]

Note that this is the maximum velocity for ideal ratchet, and it follows the expected behavior for pure diffusive motion.

Now consider probability of the protein binding is governed by equilibrium between free and bound forms:

\[ F \overset{k_a}{\underset{k_d} \rightleftharpoons} B \qquad \qquad K= \dfrac{k_a}{k_d} = \dfrac{\tau_B}{\tau_F} \nonumber \]

Here k_a refers to the effecting quasi-first-order rate constant for binding at a chaperone concentration [chap]: \(k_a = k_a' [ chap ] \).

Fast kinetics approximation

\[ \begin{aligned} &\langle \nu \rangle = \dfrac{2D}{\Delta x} \left[ \dfrac{\underset{ \sim }{f}^2/2}{\dfrac{e^{\underset{ \sim }{f}}-1}{1-K(e^{\underset{ \sim }{f}}-1)}-\underset{ \sim }{f}} \right] \\ &\langle \nu \rangle_{max} = \dfrac{2D}{\Delta x} \left( \dfrac{1}{1+2K} \right) \end{aligned} \]

Stall Load

\[ f_0 = \dfrac{k_BT}{\Delta x} \ln \left( 1+ \dfrac{1}{K} \right) \nonumber \]

________________________________

1. C. S. Peskin, G. M. Odell and G. F. Oster, Cellular motions and thermal fluctuations: the Brownian ratchet, Biophys. J. 65 (1), 316–324 (1993).