2.2: Ideal Lattice Gas
- Page ID
- 294277
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Lattice Gas
The description of a weakly interacting fluid, gas, solution, or mixture is dominated by the translational entropy or entropy of mixing. In this case, we are dealing with how molecules occupy a volume, which leads to a translational partition function. We begin by defining a lattice and the molecules that fill that lattice:
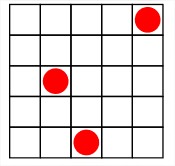
Parameters:
Total volume: \(V\)
Cell volume: \(v\)
Number of sites: \(M = V/v\)
Number of particles: \(N\ (N \le M)\)
Fill Factor: \(x = N/M\ (0 \le x \le 1)\)
Number of contacts each cell has with adjacent cells: \(z\)
We begin my assuming that all microstates (configurations of occupied sites in the volume) are equally probable, i.e., \(E_i = \text{constant}\). This is the microcanonical ensemble, so the entropy of the fluid is given by Boltzmann's equation
\[S=k_{B} \ln \Omega\]
where \(\Omega\) is the number of microstates available to the system. If \(M\) is not equal to \(N\), then the permutations for putting \(N\) indistinguishable particles into \(M\) sites is given by the binomial distribution:

Also, on cubic lattice, we have 6 contacts that each cell makes with its neighbors. The contact number is \(z\), which will vary for \(2D\ (z = 4)\) and \(3D\ (z = 6)\) problems.
How do we choose the size of \(v\)? It has to be considered on a case-by-case basis. The objective of these models is to treat the cell as the volume that a particle excludes to occupation by other particles. This need not correspond to an actual molecular dimension in the atomic sense. In the case of the traditional derivation of the translational partition function for an ideal gas, \(v\) is equivalent to the quantization volume \(\Lambda^{3}=\left(h^{2} / 2 \pi m k_{B} T\right)^{3 / 2}\).
From \(\Omega\) we can obtain the entropy of mixing from \(S = k_B \ln \Omega\) with the help of Sterling’s approximation \(\ln (M !) \simeq M \ln (M) - M\):
\[\begin{array} {rcl} {S} & = & {k_B (M \ln M - N \ln N - (M - N) \ln (M - N))} \\ {} & = & {-Mk_B (x \ln x + (1 - x) \ln (1 - x))} \end{array}\]
In the last line, we introduced a particle fill factor
\[x = N/M \nonumber\]
which quantifies the fraction of cells that are occupied by particles, and is also known as the mole fraction or the packing ratio. Since \(x < 1\), the entropy of mixing is always positive.
For the case of a dilute solution or gas, \(N \ll M\), and \((1 - x) \approx 1\), so
\[S_{\text{dilute}} \approx -N k_B \ln x \ \ \ \ or \ \ \ \ -nR \ln x\nonumber\]
We can derive the ideal gas law \(p = Nk_B T/V\) from this result by making use of the thermodynamic identity \(p = T (\partial S / \partial V)_N\).


