Entropy and Probability (Worksheet)
- Page ID
- 96613
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without accessing the Internet.
Entropy is a state function that is often erroneously referred to as the 'state of disorder' of a system. Qualitatively, entropy is simply a measure how much the energy of atoms and molecules become more spread out in a process and can be defined in terms of statistical probabilities of a system or in terms of the other thermodynamic quantities. Entropy is related to the number of available states that correspond to a given arrangement:
- A state of low entropy has a low number of states available
- A state of high entropy has a high number of states available
In an irreversible process, the universe moves from a state of low probability to a state of higher probability. We will illustrate the concepts by considering the free expansion of a gas from volume \(V_i\) to volume \(V_f\). The gas always expands to fill the available space. It never spontaneously compresses itself back into the original volume.
Two definitions:
- Microstate: a description of a system that specifies the properties (position and/or momentum, etc.) of each individual particle.
- Macrostate: a more generalized description of the system; it can be in terms of macroscopic quantities, such as P and V, or it can be in terms of the number of particles whose properties fall within a given range.
In general, each macrostate contains a large number of microstates.
Q1
Imagine a gas consisting of just two molecules and we want to consider whether the molecules are in the left (L) or right (R) half of the container.
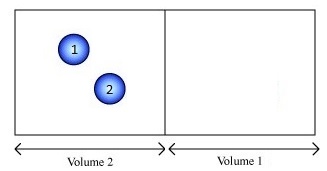


For this system, there are three macrostates:
- both molecules on the left,
- both on the right, and
- one on each side.
If we can distinguish the balls (with numbers) we have 4 microstates possible:
- L1L2
- R1R2
- L1R2
- R1L2
How many microstates are there in each macrostate?
Q2
How many macrostates and microstates are there if one molecule were in the box? How many microstates are there in each macrostate?
Q3
How many macrostates and microstates are there if three molecules were in the box? Answer given:
\[ \underbrace{L_1L_2L_3}_{\text{all L}}, \underbrace{(L_1L_2R_3, L_1R_2L_3, R_1L_2L_3)}_{\text{2 left and 1 right}}, \underbrace{(L_1R_2R_3, R_1L_2R_3, R_1R_2L_3)}_{\text{2 right and 1 left}}, \underbrace{R_1R_2R_3}_{\text{all right}}\nonumber \]
8 Microstates (above), but only 4 macrostates (below). How many microstates are there in each macrostate?
Q4
How many macrostates and microstates are there if four molecules were in the box? How many microstates are there in each macrostate?
Q5
Fill in the table below with the number of macrostates and microstates estimated in the questions above.
| Number of Molecules (N) | Microstates (W) | Macrostates (M) |
|---|---|---|
| 1 | ||
| 2 | 4 | 3 |
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Q6
Confirm that the number of microstates (W) and macrostates (M) entered in Table 1 follow the formula below for the number of molecules (N) in the box. Also, enter in the number of macrostates and microstates for N=5 to N=8; that is, complete the table.
\[W= 2^N\nonumber \]
and
\[M=N+1\nonumber \]
Weights and Probabilities
From basic combinatorics (statistics), the number of combinations of microstates with a specific permutations (i.e., for picking \(n\) items from \(N\) total) is given by
\[W_{N,n} = \dfrac{N!}{n!(N-n)!} \label{combo} \]
where ! is factorial and is the product of an integer and all the integers below it (e.g., 4! = 24). W is called the weight or “multiplicity” of this microstate and the sum of weights per macrostate equals the total number of microstates for the system:
\[W = 2^N = \sum_n W_{N,n} = \sum_n \dfrac{N!}{n!(N-n)!}\nonumber \]
If we assume all microstates are equally probable. then the probability \(P(N,n)\) of observing a specific macrostate \(n\) is
\[ P(N,n)= \dfrac{W_{N,n}}{2^N}\nonumber \]
Thus, we can calculate the likelihood of finding a given arrangement of molecules in the container. For example, the weight of the configuration of 2 molecules on the left side of a box with 6 molecules in it is:
\[ W_{6,2} = \dfrac{6!}{2!4!} = 15\nonumber \]
and the probability of this state being observed is
\[ W_{6,2}/2^N = \dfrac{15}{64}= 0.234\nonumber \]
or there is a 23.4% chance of observing this state.
Q7
- What is the probability of observing each of possible macrostates for a 5 particle in a box system?
- Which macrostate has the lowest probability of being observed?
- Which macrostate has the highest probability of being observed?
Entropy and Weights
Events such as the spontaneous compression of a gas (or spontaneous conduction of heat from a cold body to a hot body) are not impossible, but they are so improbable that they never occur. We can relate the weight (W) of a system to its entropy \(S\) by considering the probability of a gas to spontaneously compress itself into a smaller volume.
If the original volume is \(V_i\), then the probability of finding \(N\) molecules in a smaller volume \(V_f\) is
\[P = \dfrac{W_f}{W_i} = \left(\dfrac{V_f}{V_i} \right)^N\nonumber \]
taking the natural logarithm
\[\ln\left( \dfrac{W_f}{W_i} \right) = N \ln\left( \dfrac{V_f}{V_i} \right) = n N_A \ln \left( \dfrac{V_f}{V_i} \right)\nonumber \]
For a free expansion of an ideal gas (take for granted at this time)
\[\Delta S = n R \ln \left( \dfrac{V_f}{V_i} \right)\nonumber \]
so inserting the relationship with weights
\[\Delta S = (R/N_A) \ln \left( \dfrac{W_f}{W_i} \right) = k \ln\left( \dfrac{W_f}{W_i} \right)\nonumber \]
or via properties of logarithms
\[S_f - S_i = k \ln W_f - k \ln W_i \nonumber \]
Thus, we arrive at an equation, first deduced by Ludwig Boltzmann, relating the entropy of a system to the number of microstates:
\[S = k \ln(W) \nonumber \]
He was so pleased with this relation that he asked for it to be engraved on his tombstone (and it is).
Q8
What is the entropy of each of the macrostates tabulated in Q7? What is the change in entropy for an expansion of all balls (molecules) originally in half the volume of the box into the full box?

