Ksp and Calcium Fortification

Orange juice

Yogurt sauce

Sardines

An adequate dietary calcium intake is necessary to achieve peak bone mass and minimize bone loss with aging.^[1] The adequate intake of calcium is 1300 mg/day, but it may vary depending on gender and age. ^[2] Besides its role in bone health, calcium has been associated with low risk of colorectal cancer^[3] and low blood pressure.^[4] On the other hand, an excess in the consumption of dietary calcium can decrease the absorption of other minerals such as iron, phosphorus, magnesium, and zinc.^[5] An intake of dietary calcium above 2000 mg/day has been linked to prostate cancer.^[6]

Vitamin D and phosphorous, the other bone forming mineral, are two key factors affecting the metabolism of calcium in bone. Calcium and phosphorous must exist in adult diets in a molar ratio of Ca:P (or 1.3 weight ratio) to ensure adequate bone health.^[7]However in many countries, the consumption of P is higher to that of calcium resulting in low Ca:P dietary ratios.^[8] In animal models, low Ca:P ratios have been associated to hyperparathyroidism (cause for high levels of calcium in blood), loss of bone, and osteopenia (lower than normal bone mineral density). In contrast, high Ca:P ratios seem to be favorable to bone mineralization. In women with adequate calcium intake, low Ca:P molar ratios of 0.5 or less resulted in higher serum parathyroid hormone and urinary calcium level. Such conditions could disturb Ca metabolism and bone health. In the cited study, however, the participants with a high Ca intake did not achieve Ca:P ratio of 1 and Ca:P ratios above 0.5 would be sufficient if the calcium intake is at the recommended level.^[9]

Foods naturally rich in calcium include sardines, yogurt, cheese, and milk. However, in response to the importance of calcium in the diet, processing companies are supplementing numerous food products with this mineral. Some of the factors to take into account when adding calcium salts in formulations are taste, mouthfeel, calcium content of the salt, and interactions of calcium with other food components. Calcium salts in excess may contribute with a soapy taste especially in high fat foods subjected to heating (saponification), they may also result in gritty or chalky mouthfeel due to their low solubility. Calcium bioavailability is reduced by the presence of phosphates, phytic, and oxalic acids and in some cases it is only absorbed with meals. Finally, calcium may interact with proteins and some polysaccharides (pectins) present in the food resulting in a firmer structure.

Sources of phosphorous in the diet include cola beverages and processed foods which may contain several phosphates. Calcium phosphates are widely used in processed foods as leavening, anticacking, and buffering agents. Examples of these additives are tricalcium phosphate, calcium carbonate, monocalcium phosphate, and dicalcium phosphate. When evaluating the actual consumption of calcium and phosphorous, it is necessary to take into account the amounts provided by food additives consumed in the diet. Given the importance of the Ca:P ratio, salts other than phosphates can be used as calcium supplements. Some alternatives are oxalates, lactates, citrates, and carbonates. However, some of these anions may bind and lower the bioavailability of other important minerals such as iron and magnesium.

The solubility of calcium salts is highly dependent on pH and changes of this parameter during processing or storage can favor salt precipitation. Strategies to prevent it include combining calcium salts containing different anions, control the pH, and adding sequestering salts such as citrates. Again, some of these factors can reduce calcium bioavailability and obtaining calcium supplemented foods with the desired balance between sensory profile and nutritional quality requires careful consideration of the interactions between calcium and other food components.

How do we calculate the solubility of salts with limited solubility?

Calcium oxalate, one of many salts with very limited water solubility, is a compound implicated in the formation of kidney stones. When CaC₂O₄ crystals are shaken with water, so little dissolves that it is impossible to see that anything has happened. Nevertheless, the few Ca²⁺(aq) and C₂O₄^2–(aq) ions that do go into solution increase the conductivity of the water, allowing us to measure their concentration. We find that at 25°C

\[[\text{Ca}^{2+}] = \text{4.82} \times \text{10}^{-5} \text{mol dm}^{-3} = [\text{C}_2\text{O}_4^{2-}]\label{1}\]

so that we would describe the solubility of CaC₂O₄H₂O as 4.82 × 10^–5 mol dm^–3 at this temperature. The solid salt and its ions are in dynamic equilibrium, and so we can write the equation

\[\ce{CaC2O4 (s) <-> Ca^{2+}(aq) + C2O4^{2-} (aq)}\]

As in other dynamic equilibria, a particular Ca²⁺ ion will sometimes find itself part of a crystal and at other times find itself hydrated and in solution.

Since the concentration of CaC₂O₄•H₂O has a constant value, it can be incorporated into K_c for Eq. (2). This gives a special equilibrium constant called the solubility product K_sp:

\[\text{K}_{sp} = \text{K}_c [\text{CaC}_2\text{O}_4] = [\text{Ca}^{2+}][\text{C}_2\text{O}_4^{2-}]\label{3}\]

For CaC₂O₄, K_sp is easily calculated from the solubility by substituting Eq. \(\ref{1}\) into \(\ref{3}\):

\[\text{K}_{sp} = (\text{4.82} \times \text{10}^{-5} \text{mol dm}^{-3}) (\text{4.82} \times \text{10}^{-5} \text{mol dm}^{-3}) = \text{2.32} \times \text{10}^{-9} \text{mol}^2 \text{dm}^{-6}\nonumber\]

In the general case of an ionic compound whose formula is A_xB_y, the equilibrium can be written

\[\text{A}_x\text{B}_y(s) \rightleftharpoons x\text{A}^{m+}_{(aq)} + y\text{A}^{n+}_{(aq)} \]

The solubility product is then

\[\text{K}_{sp} = [\text{A}^{m+}]^x[\text{B}^{n+}]^y\]

Example \(\PageIndex{1}\): Calcium Lactate Crystals

When crystals of calcium lactate (Ca(C₃H₅O₃)₂) are shaken with water at 16.7°C, it was found that after five days, 1.6 × 10^–2 mol Ca(C₃H₅O₃)₂ dissolved per cubic decimeter of solution.^[10] Find the value of K_sp at this temperature.

Solution We first write out the equation for the equilibrium:

\[\ce{Ca(C3H5O3)2 (s) <-> Ca(2+) (aq) + 2C3H5O3- (aq)}\]

so that

\[\text{K}_{sp} (\text{Ca(C}_3\text{H}_5\text{O}_3)_2) = [\text{Ca}^{2+}][\text{C}_3\text{H}_5\text{O}_3 ^{-}]^2 \]

Since 1.6 × 10^–2 mol Ca(C₃H₅O₃)₂ dissolves per cubic decimeter, we have

\[[\text{Ca}^{2+}] = \text{1.6} \times \text{10}^{-2} \text{mol dm}^{-3}\nonumber\]

while

\[[\text{C}_3\text{H}_5\text{O}_3 ^{-}] = 2 \times \text{1.6} \times \text{10}^{-2} \text{mol dm}^{-3}\nonumber\]

since 2 mol C₃H₅O₃^– ions are produced for each mol Ca(C₃H₅O₃)₂ which dissolves. Thus

\[\text{K}_{sp} = (\text{1.6} \times \text{10}^{-2} \text{mol dm}^{-3}) (2 \times \text{1.6} \times \text{10}^{-2} \text{mol dm}^{-3}) = \text{1.64} \times \text{10}^{-5} \text{mol}^3 \text{dm}^{-9}\nonumber\]

Calcium sulfite

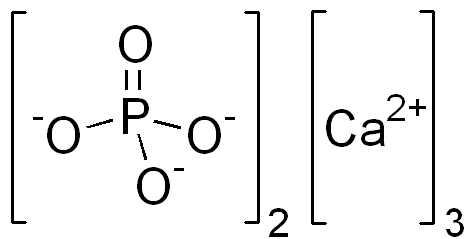
Tricalcium phosphate

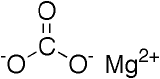
Magnesium carbonate

Table \(\PageIndex{1}\)/ Some low solubility salts used in processed foods[1] [2]

Salt	Formula	Function	Foods	Ksp
Calcium sulphate	CaSO4	Emulsifying salt, thickener, coagulant in tofu production	Dairy products, breakfast cereals, fat emulsions	4.93x10^-5
Calcium sulfite	CaSO3	Source of sulfur dioxide, antimicrobial, and enzyme inhibitor	Fruit juice, wine, and other fruit beverages	3.1x10^-7
Iron (III) phosphate dihydrate	FePO4•2H2O	Supplement, source of iron	Various	9.91x10^-16
Magnesium carbonate pentahydrate	MgCO3•5H2O	Anticacking agent, color retention	Dry whey and whey products	3.79x10^-14
Magnesium hydroxide	Mg(OH)2	Color retention, acidity regulator	Processed fruits and various	5.61x10^-12

The solubility products for some of the more common sparingly soluble inorganic compounds are given here.

Example \(\PageIndex{2}\): Solubility of a Salt

The solubility product of tricalcium phosphate, Ca₃(PO₄)₂, is 2.0 × 10^–29 mol⁵ dm^–15. Find the solubility of this salt.

Solution

Again we start by writing the equation

\[\ce{Ca3(PO4)2 (s) <-> 3Ca^(2+) (aq) + 2PO4 ^(3-) (aq)}\nonumber\]

from which

\[\text{K}_{sp}(\text{Ca}_3(\text{PO}_4)_2) = [\text{Ca}^{2+}]^3[\text{PO}_4^{3-}]^2 = \text{2.0} \times \text{10}^{-29} \text{mol}^5 \text{dm}^{-15}\nonumber\]

Let the solubility be x mol dm^–3. Then

\([\text{PO}_4^{3-}] = 2x \text{mol dm}^{-3}\) and \([\text{Ca}^2+] = 3x \text{mol dm}^{-3}\)

Thus

\[\text{K}_{sp} = (3x \text{mol dm}^{-3})^3( 2x \text{mol dm}^{-3})^2\nonumber\]

\[ = (3x)^3(2x)2 \text{mol}^5\text{dm}^{-15} = \text{2.0} \times \text{10}^{-29} \text{mol}^3\text{dm}^{-9}\nonumber\]

or \(\text{108}x^5 = \text{2.0} \times \text{10}^{-29}\)

and

\[x^5 = \dfrac{\text{2.0}}{\text{108}} \times \text{10}^{-29} = \text{1.85} \times \text{10}^{-31} = \text{185} \times \text{10}^{-33}\nonumber\]

so that \( x = \text{7.13} \times \text{10}^{-7}\)

Thus the solubility of tricalcium phosphate is 7.13 × 10^–7 mol dm^–3.

From ChemPRIME: 14.10: The Solubility Product

References

1. ↑ www.codexalimentarius.net/gsf...s/index.html#M
2. ↑ Food Additives, 2nd ed. 2002, Branen, A., Davidson, M.P., Salminen, S. and Thorngate III, J.H.

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.