Laser Radiation Properties
- Page ID
- 74652
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Laser Radiation Properties I
- Laser radiation is nearly monochromatic. Monochromatic refers to a single wavelength, or “one color” of light. Laser radiation contains a narrow band of wavelengths and can be produced closer to monochromatic than light from other sources.
- Laser radiation is highly directional. The radiation is produced in a beam that is spatially narrow and has low divergence relative to other light sources.
- Laser radiation is highly coherent, which means the waves of light emitted have a constant relative phase. The waves of light in a laser beam are thought of as in phase with one another at every point. The degree of coherence is proportional to the range of wavelengths in the light beam, or the beam’s monochromaticity. Laser radiation has both spatial and temporal coherence, characterized by the coherence length and the coherence time.
Coherence

- Temporal coherence is the ability of light to maintain a constant phase at one point in space at two different times, separated by delay τ. Temporal coherence characterizes how well a wave can interfere with itself at two different times and increases as a source becomes more monochromatic.
- A coherence time (τcor) and coherence length (c × τcor, where c is the speed of light) can be calculated from the spread of wavelengths (Δλ), or frequencies (Δν), in a beam. Expressed in terms of Δν, or “bandwidth”:
\[\tau_{cor} = \dfrac{1}{2 \pi Δν}\]
Laser Radiation Properties II
- Laser radiation has high brightness, a quantity defined as the power emitted per unit surface area per unit solid angle. Because laser light is emitted as a narrow beam with small divergence, the brightness of a 1 mW laser pointer, for example, is > 1,000 ×’s greater than that of the sun, which emits more than 1025 W of radiant power a.
- Laser output can be continuous or pulsed. Continuous wave (CW) lasers are characterized by their average power, whereas peak power, energy per pulse and pulse repetition rate are figures of merit that apply to pulsed lasers. Pulse widths in the ns-ps range are employed more routinely than fs pulses, and attosecond pulses can be generated. A 10 fs pulse with only 10 mJ energy has a peak power of 1012 W, or 1 TW!
Laser Radiation Properties III
- The narrow range of frequencies, or wavelengths, emitted is referred to as the laser bandwidth. This output is determined by the spectral emission properties of the gain medium and the modes supported by the cavity.
- When the bandwidth of the gain medium is larger than the cavity mode spacing, the laser output consists of a series of narrow spectral bands (see the following figure and “Laser Radiation Properties IV” below).
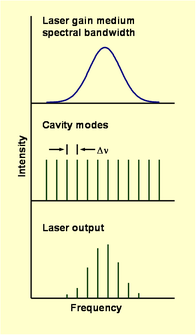
- Cavity modes develop as a consequence of the properties of light reflection and interference. In the simplest case of a cavity formed by two flat mirrors, the allowable axial modes have wavelength λ = 2L/q, where L is the cavity length and q is an integer. The frequency spacing (Δν) between modes is given by Δν = c/(2L), where c is the speed of light. Parabolic mirrors produce more complex cavity modes leading to a Gaussian beam b.
Laser Radiation Properties IV
Laser bandwidth frequency (Δν) and wavelength (Δλ) are related as follows:
\[\Delta \lambda \approx\left(\frac{\lambda_{0}^{2}}{c}\right) \Delta v\]
where λo is the band center wavelength and c is the speed of light. A HeNe laser operating at 632.8 nm has a gain bandwidth of 1.5 GHz, or 0.002 nm. When the gain medium bandwidth is smaller than the cavity mode spacing, the laser output consists of a single mode and operates as a single frequency laser c.
- A HeNe laser with 20 cm cavity length has mode spacings of Δν = 750 MHz, or Δλ = .001 nm. HeNe lasers are often equipped for and use single frequency operation c, d.
- Mode locking e produces a fixed phase relationship between laser cavity modes and results in pulsed output. See Refs [2,7,8,9] for more details on mode locking and methods for producing ultra-short laser pulses and other aspects of single frequency laser operation.


