Reduction Potential Intuition

Reduction potentials are relative and are reported relative to the reduction of protons in a standard hydrogen electrode (SHE) in Tables P1 and P2. However, what would we see if we used some other sort of electrode for comparison? For example, instead of a hydrogen electrode, we might use a fluorine electrode, in which we have fluoride salts and fluorine gas in solution with a platinum electrode. The "reduction potentials" we measure would all be relative to this reaction now. They would tell us: how much more motivated is this ion to gain an electron than fluorine? The resulting table would look something like this:

Table \(\PageIndex{1}\): Standard Reduction Potentials

Half Reaction (species are aqueous unless noted otherwise)	Potential, Volts, Relative to Fluorine Reduction
Li^+ + e^- \(\rightleftharpoons\) Li (s)	- 5.91
Al(OH)3(s) + 3e^- \(\rightleftharpoons\) Al(s) + 3OH^-	- 5.18
Sc^3^+ + 3e^- \(\rightleftharpoons\) Sc (s)	- 4.95
Al^3^+ + 3e^- \(\rightleftharpoons\) Al (s)	- 4.53
V^2^+ + 2e^- \(\rightleftharpoons\) V (s)	- 4.00
Zn^2^+ + 2e^- \(\rightleftharpoons\) Zn (s)	- 3.632
Fe^2^+ + 2e^- \(\rightleftharpoons\) Fe (s)	- 3.31
CO2(g) + 2H^+ + 2 e^- \(\rightleftharpoons\) CO(g) + H2O	- 2.98
Cu^+ + e^- \(\rightleftharpoons\) Cu (s)	- 2.98
2 H^+ + 2 e^- \(\rightleftharpoons\) H2(g)	- 2.87
Fe3O4(s) + 8 H^+ + 8 e^- \(\rightleftharpoons\) 3Fe(s) + 4 H2O	- 2.79
Cu^2^+ + 2e^- \(\rightleftharpoons\) Cu^0	- 2.53
CO(g) + 2H^+ + 2 e^- \(\rightleftharpoons\) C(s) + H2O	- 2.35
MnO4^- + 2 H2O + 3e^- \(\rightleftharpoons\) MnO2(s) + 4 OH^-	- 2.28
Fe^3^+ + e^- \(\rightleftharpoons\) Fe^2^+	- 2.10
Ag^+ + e^- \(\rightleftharpoons\) Ag (s)	- 2.074
MnO2 + 4 H^+ + 2e^- \(\rightleftharpoons\) Mn^2^+ + 2 H2O	- 1.64
MnO4^- + 4 H^+ + 3e^- \(\rightleftharpoons\) MnO2(s) + 2 H2O	- 1.17
Au^+ + e^- \(\rightleftharpoons\) Au (s)	- 1.04
F2 (g) + 2e^- \(\rightleftharpoons\) 2F^-	0.00

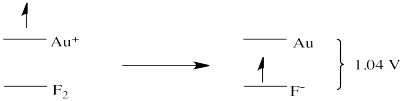
The trouble is, there is not much out there that would be more motivated than fluorine to gain an electron. All of the potentials in the table are negative because none of the species on the left could take an electron away from fluoride ion. However, if we turned each of these reactions around, the potentials would all become positive. That means gold, for instance, could give an electron to fluorine to become \(\ce{Au^{+}}\). This electron transfer would be spontaneous, and a voltmeter in the circuit between the gold electrode and the fluorine electrode would measure a voltage of -1.04 V.

That potential is generated by the reaction:

\[ \ce{ 2 Au (s) + F_2 (g) -> 2 Au^{+} + 2 F^{-}} \nonumber \]

Notice that, because 2 electrons are needed to reduce the fluorine to fluoride, and because gold only supplies one electron, two atoms of gold would be needed to supply enough electrons.

The reduction potentials in Table \(\PageIndex{1}\) are, indirectly, an index of differences in electronic energy levels. The electron on gold is at a higher energy level than if it were on fluoride. It is thus motivated to spontaneously transfer to the fluorine atom, generating a potential in the circuit of -1.04V.

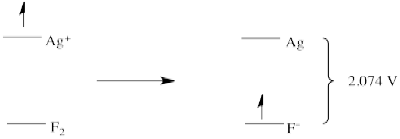
Silver metal is even more motivated to donate an electron to fluorine. An electron from silver can "fall" even further than an electron from gold, to a lower energy level on fluoride. The potential in that case would be - 2.074 V.

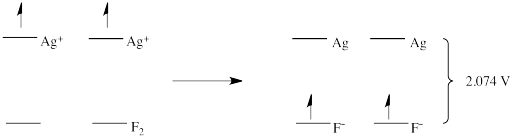
There are a couple of things to note here. The first is that, if potential is an index of the relative energy level of an electron, it does not matter whether one electron or two is transferred. They are transferred from the same, first energy level to the same, second energy level. The distance that the electron falls is the same regardless of the number of electrons that fall. A reduction potential reflects an inherent property of the material and does not depend on how many electrons are being transferred.

• Reduction potentials reflect the energy difference between two states
• The difference between those two states involves an exchange of one or more electrons
• Frequently, the reduction potential simply reflects the energy level of the electron in one state versus the other (although we will see other factors later)
• The number of electrons transferred does not affect the energy difference between the two states, and so does not affect the reduction potential
• The number of electrons would affect the overall energy gained / released during the electron transfer reaction (because ΔG = - nFE)

Another important note is that, if reduction potentials provide a glimpse of electronic energy levels, we may be able to deduce new relationships from previous information. For example, if an electron on gold is 1.04 V above an electron on fluoride, and an electron on silver is 1.04 V above an electron on fluoride, what can we deduce about the relative energy levels of an electron on silver vs. gold?

The answer is that the electron on silver is 1.034 V above the electron on gold. We know this because reduction potentials are "state functions", reflecting an intrinsic property of a material. It does not matter how we get from one place to another; the answer will always be the same. That means that if we transfer an electron from silver to gold indirectly, via fluorine, the overall potential will be the same as if we transfer the electron directly from silver to gold. So, the electron drops from silver to fluorine (a drop of 2.074 V). The electron then hops (under duress) up to gold (a climb of 1.04 V). The net drop is only 1.034 V.

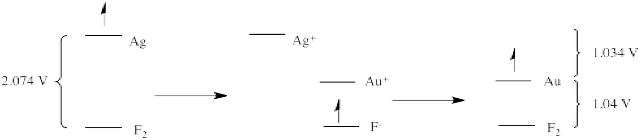
That's the same value we would expect to measure if we took a standard solution of gold salts and a gold electrode and connected it, via a circuit, to a standard solution of silver salts and a silver electrode.

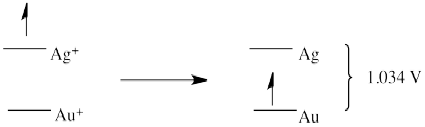
In fact, the table above does not reflect any experimental measurements; it's simply the table of standard reduction potentials from the previous page, with the reduction potential of fluorine subtracted from all the other values.

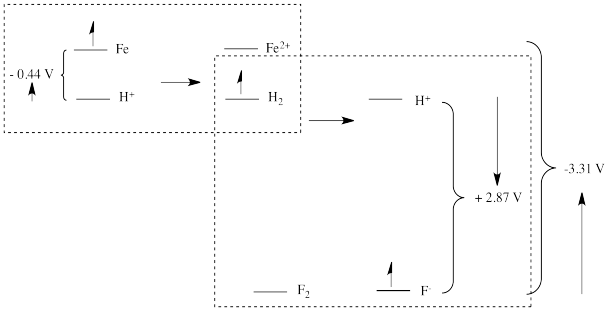
In other words, mapping out the distance from iron to SHE (in terms of the reduction potential for \(Fe^{2+} + 2 e^- \rightarrow Fe(s)\)), together with the distance from SHE to fluorine gives the potential relative to IFE (imaginary fluorine electrode).

Problems

1

1. Show an energy diagram showing the relative energy levels when an electron is transferred from silver to gold(I) ion. What is the potential for this reaction?
2. Show an energy diagram showing the relative energy levels when an electron is transferred from copper to silver(I) ion. What is the potential for this reaction?
3. Show how the results of (a) and (b) can be used to determine the potential for the transfer of an electron from copper to gold(I) ion.

2

Frequently in biology, electron transfers are made more efficient through a series of smaller drops rather than one big jump. To think about this, consider the transfer of an electron from lithium to fluorine. (Neither of these species is likely to be found in an organism, but this transfer is a good illustration of a big energy difference.)

1. Write an equation for this reaction.
2. What would be the potential for this reaction?
3. This is a highly exothermic reaction; however, our imaginary organism that attempts to harness this reaction as an energy source is likely to burst into flames every time the reaction occurs. Comment on the organism's Darwinian fate.
4. Propose, instead, a series of reactions that the organism could use to slow down the release of energy. Suppose the organism, apart from fluorine and lithium, also harbors reserves of scandium(III), silver(I), copper(I), vanadium(II) and gold(I). Show an energy diagram for this series of reactions and label the potential for each step.
5. Explain why this approach would more efficiently harness the energy of lithium's electron.

3

An "activity series" is a ranking of elements in terms of their "activity" or their ability to provide electrons. The series is normally written in a column, with the strongest reducing metals at the top. Beside these elements, we write the ion produced when the metal loses its electron(s). Looking at the table of reduction potentials relative to fluorine on this page, construct an activity series for the available elements.

4

Construct an activity series for the alkali metals using the following standard reduction potentials (relative to SHE): Fr, -2.9 V; Cs, -3.026 V; Rb, -2.98 V; K, -2.931 V; Na, -2.71 V; Li, -3.04 V.

5

In reality, the energy gap that leads to a reduction potential is sometimes more complicated than following an electron as it moves from one level to another. Use the activity series you have constructed for the alkali metals to compare and contrast the redox potential with your expectations of energy level / ease of electron donation based on standard periodic trends.

Contributors and Attributions

• Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)