Nonstandard Conditions: The Nernst Equation

The standard cell potentials refer to cells in which all dissolved substances are at unit activity, which essentially means an "effective concentration" of 1 M. Similarly, any gases that take part in an electrode reaction are at an effective pressure of 1 atm. If these concentrations or pressures have other values, the cell potential will change in a manner that can be predicted from the principles you already know.

Cell potentials depend on Concentrations

Suppose, for example, that we reduce the concentration of \(Zn^{2+}\) in the \(Zn/Cu\) cell from its standard effective value of 1 M to an to a much smaller value:

Zn(s) | Zn²⁺(aq, .001M) || Cu²⁺(aq) | Cu(s)

This will reduce the value of \(Q\) for the cell reaction

Zn(s) + Cu²⁺ → Zn²⁺ + Cu(s)

thus making it more spontaneous, or "driving it to the right" as the Le Chatelier principle would predict, and making its free energy change \(\Delta G\) more negative than \(\Delta G°\), so that E would be more positive than E°.

The relation between the actual cell potential E and the standard potential E° is developed in the following way. We begin with the equation derived previously which relates the standard free energy change (for the complete conversion of products into reactants) to the standard potential

\[\Delta G° = –nFE° \nonumber \]

By analogy we can write the more general equation

\[\Delta G = –nFE \nonumber \]

which expresses the change in free energy for any extent of reaction— that is, for any value of the reaction quotient \(Q\). We now substitute these into the expression that relates \(\Delta G\) and \(\Delta G°\) which you will recall from the chapter on chemical equilibrium:

\[\Delta G = \Delta G° + RT \ln Q \nonumber \]

which gives

\[–nFE = –nFE° + RT \ln Q \nonumber \]

which can be rearranged to

\[ E=E° -\dfrac{RT}{nF} \ln Q \label{1} \]

This is the Nernst equation that relates the cell potential to the standard potential and to the activities of the electroactive species. Notice that the cell potential will be the same as \(E°\) only if \(Q\) is unity. The Nernst equation is more commonly written in base-10 log form and for 25 °C:

\[ E=E° -\dfrac{0.059}{n} \log_{10} Q \label{2} \]

The equation above indicates that the electrical potential of a cell depends upon the reaction quotient \(Q\) of the reaction. As the redox reaction proceeds, reactants are consumed, thus concentration of reactants decreases. Conversely, the products concentration increases due to the increased in products formation. As this happens, cell potential gradually decreases until the reaction is at equilibrium, at which \(\Delta{G} = 0\).

Significance of the Nernst eqation

The Nernst equation tells us that a half-cell potential will change by 59 millivolts per 10-fold change in the concentration of a substance involved in a one-electron oxidation or reduction; for two-electron processes, the variation will be 28 millivolts per decade concentration change.

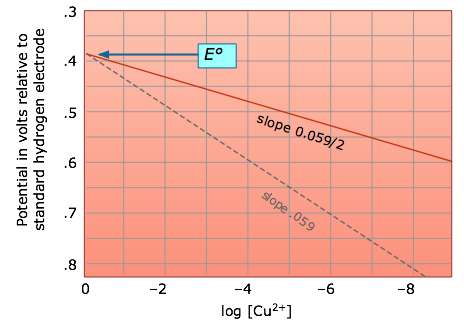
Thus for the dissolution of metallic copper

Cu(s) → Cu²⁺ + 2e^–

the potential

E = (– 0.337) – .0295 log [Cu²⁺]

becomes more positive (the reaction has a greater tendency to take place) as the cupric ion concentration decreases. This, of course, is exactly what the Le Chatelier Principle predicts; the more dilute the product, the greater the extent of the reaction.

Example \(\PageIndex{1}\):

Consider the Zn-Cu redox reaction:

\[Zn_{(s)} + Cu^{2+}_{(aq)} \rightarrow Zn^{2+}_{(aq)} + Cu_{(s)} E^{o}_{cell} = +1.10 \; V \nonumber \]

Solution

Initially, [Cu²⁺] = [Zn²⁺] = 1.0 M at standard T = 298K As the reaction proceeds, [Cu²⁺] decreases as [Zn²⁺] increases. Lets say after one minute, [Cu²⁺] = 0.05 M while [Zn²⁺] = 5.0 M. According to Nernst, cell potential after 1 minute is:

\[E = E^o - \dfrac{0.0592 V}{n} \log Q \nonumber \]

\[E = 1.10V - \dfrac{0.0592 V}{2} \log\dfrac{5.0 \; M}{.05 \; M} \nonumber \]

\[E = 1.04 \; V \nonumber \]

As you can see, the initial cell potential is \(E = 1.10\, V\), after 1 minute, the potential drops to 1.04 V. As the reaction continues to progress, more Cu²⁺ will be consumed and more Zn²⁺ will be generated. As a result, the cell potential continues to decrease and when the cell potential drops down to 0, the concentration of reactants and products stops changing. This is when the reaction is at equilibrium.

At equilibrium, the reaction quotient \(Q = K_{eq}\). Also, at equilibrium, \(\Delta{G} = 0\) and \(\Delta{G} = -nFE\), so \(E = 0\).

Therefore, substituting \(Q = K_{eq}\) and \(E = 0\) into the Nernst equation, we have:

\[0 = E^o - \dfrac{RT}{nF} \ln K_{eq} \nonumber \]

At standard conditions, the equation above simplifies into:

\[0 = E^o - \dfrac{0.0592}{n} \log K_{eq} \nonumber \]

This equation can be rearranged into:

\[log K_{eq} = \dfrac{nE^o}{0.0592} \nonumber \]

The equation above indicates that the equilibrium constant K_eq is proportional to the standard potential of the reaction. Specifically, when:

• \(K > 1, E^o > 0\), reaction favors products formation.
• \(K < 1, E^o < 0\), reaction favors reactants formation.

This result fits Le Châtlier's Principle, which states that when a system at equilibrium experiences a change, the system will minimize that change by shifting the equilibrium in the opposite direction.

Outside Links

• Feiner, A.-S.; McEvoy, A. J. "The Nernst Equation." J. Chem. Educ. 1994, 71, 493.
• Thompson, Martin L.; Kateley, Laura J. "The Nernst Equation: Determination of Equilibrium Constants for Complex Ions of Silver." J. Chem. Educ. 1999 76 95.