Half-Cell Reaction
- Page ID
- 36510
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Explain chemical reactions for each electrode of a battery or galvanic cell.
- Use notations to depict an electrode.
- Describe oxidation and reduction reactions.
- Construct a hydrogen electrode.
Half Cell Reactions
A half cell is one of the two electrodes in a galvanic cell or simple battery. For example, in the \(\ce{Zn-Cu}\) battery, the two half cells make an oxidizing-reducing couple. Placing a piece of reactant in an electrolyte solution makes a half cell. Unless it is connected to another half cell via an electric conductor and salt bridge, no reaction will take place in a half cell.
On the cathode, reduction takes place.
- \(\ce{Oxidant + n\: e^- \rightarrow Reductant}\)
- Example: \(\ce{Cu^2+ + 2 e^- \rightarrow Cu}\)
- \(\ce{Cu^2+}\) is the oxidizing agent and \(\ce{Cu}\) the reducing agent.
On the anode, oxidation takes place.
- \(\ce{Reductant \rightarrow Oxidant + n\: e^-}\)
- Example: \(\ce{Zn \rightarrow Zn^2+ + 2 e^-}\).
- \(\ce{Zn}\) is the reducing agent, and \(\ce{Zn^2+}\) the oxidizing agent.
A battery requires at least two electrodes, the anode at which oxidation occurs, and the cathode at which reduction occurs. Reduction and oxidation are always required in any battery setup.
A battery operation requires an anode, a cathode, a load, and a salt bridge (if the salt bridge is not there already). These are the key elements of a battery.
Write the anode and cathode reactions for a galvanic cell that utilizes the reaction
\(\ce{Ni_{\large{(s)}} + 2 Fe^3+ \rightarrow Ni^2+ + 2 Fe^2+}\)
Solution
Oxidation takes place at the anode, and the electrode must be \(\ce{Ni\, |\, Ni^2+}\),
\(\ce{Ni_{\large{(s)}} \rightarrow Ni^2+_{\large{(aq)}} + 2 e^-}\)
and the reduction occurs at the cathode: \(\ce{Fe^3+,\: Fe^2+}\):
\(\ce{2 Fe^3+ + 2 e^- \rightarrow 2 Fe^2+}\)
For every \(\ce{Ni}\) atom oxidized, two \(\ce{Fe^3+}\) ions are reduced. The electrons from the \(\ce{Ni}\) metal will flow from the anode, pass the load, and then carry out the reduction at the surface of the cathode to reduce the ferric (\(\ce{Fe^3+}\)) ions to ferrous ions. In the meantime the ions in the solution move accordingly to keep the charges balanced.
Discussion
The galvanic cell is:
\(\ce{Ni_{\large{(s)}}\, |\, Ni^2+_{\large{(aq)}}\, ||\, Fe^3+_{\large{(aq)}},\: Fe^2+_{\large{(aq)}}\, |\, Pt_{\large{(s)}}}\)
where "\(\ce{Fe^3+_{\large{(aq)}},\: Fe^2+_{\large{(aq)}}}\)" represents a solution containing two types of ions. An inert \(\ce{Pt}\) electrode is placed in the solution to provide electrons for the reduction.
The charge on an electron is 1.602x10-19 C (coulomb). What is the charge on 1 mole of electrons?
Solution
The charge on one mole (Avogadro's number of) electrons is called a Faraday (F).
\(\begin{align}
F &= (6.022045\times10^{23} / \ce{mol}) \times (1.602\times10^{-19}\: \ce C)\\
&= \textrm{96485 C/mol}
\end{align}\)
The chemical history involving the determination of Avogadro's number, and the charge on an electron, and how the two values agree with each other is very interesting.
Discussion
Who determined the charge on a single electron? Robert Millikan was awarded with the Nobel Prize for his determination of electron charge at University of Chicago.
If 96485 C of charge is required to deposit 107.9 g of silver, what is the charge of an electron?
A galvanic cell with a voltage of 1.1 V utilizes the reaction
\(\ce{Zn + Cu^2+ \rightarrow Cu + Zn^2+}\)
as a source of energy. If 6.3 g of \(\ce{Cu}\) and 11 g \(\ce{Zn}\) are used, what is the maximum usable energy in this battery?
Solution
The 6.3 g \(\ce{Cu}\) and 11 g \(\ce{Zn}\) correspond to 0.10 and 0.17 mol of \(\ce{Cu}\) and \(\ce{Zn}\) respectively. Thus, \(\ce{Cu}\) is the limiting reagent, and 0.10 mol corresponds to a charge of 2×96485×0.10 C (2 significant figures). The maximum available energy is then
\(\begin{align}
\textrm{Max. Energy} &= \mathrm{(1.1\: V)(96485\: C)(2)(0.10)}\\
&= \mathrm{22000\: J \hspace{15px} (1\: J = 1\: VC)}
\end{align}\)
Discussion
This energy corresponds to 2500 cal, which is enough to bring 25 g water from 273 K to its boiling point (373 K). Another way of looking at it: 22000 J is enough energy to send a 20-gram rocket to a height of 56 m.
If the galvanic cell of Example 3 is used to power a calculator, which consumes 1 mW, how long theoretically will the battery last in continuous operation?
Solution
Power consumption of 1 mW is equivalent to 0.001 J/sec.
\(\begin{align}
\mathrm{\dfrac{22000\: J}{0.001\: J/sec}} &= \textrm{2.2E7 sec}\\
&= \textrm{6200 hrs}\\
&= \textrm{254 days}
\end{align}\)
This is a realistic example. Most recent calculators use very little power. I noted that a SHARP programmable calculator uses 15 mW, a Casio calculator uses 0.5 mW, and an HP 25 uses 500 mW.
The Hydrogen Half Cell
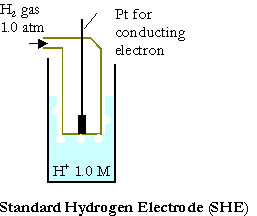 A half cell consists of an electrode and the species to be oxidized or reduced. If the material conducts electricity, it may be used as an electrode. The hydrogen electrode consists of a \(\ce{Pt}\) electrode, \(\ce{H2}\) gas and \(\ce{H+}\). This half cell is represented by:
A half cell consists of an electrode and the species to be oxidized or reduced. If the material conducts electricity, it may be used as an electrode. The hydrogen electrode consists of a \(\ce{Pt}\) electrode, \(\ce{H2}\) gas and \(\ce{H+}\). This half cell is represented by:
\(\ce{Pt_{\large{(s)}}\, |\, H_{2\large{(g)}}\, |\, H+_{\large{(aq)}}}\)
where the vertical bars represent the phase boundaries. Conventionally, the cell potential for the hydrogen electrode is defined to be exactly zero if it has the condition as given below:
\(\ce{Pt\, |\, H_{2\: \large{(g,\: 1\: atm)}}\, |\, H+_{\large{(aq)}},\: 1\: M}\)
The notations for half cells are not rigid, but a simplified way to represent a rather complicated setup.
Standard Reduction Potential
The tendency for a reduction reaction is measured by its reduction potential.
- \(\ce{Oxidant + n\: e^- \rightarrow Reductant} \hspace{15px} E^{\ce o}\)
- For example: \(\ce{Cu^2+ + 2 e^- \rightarrow Cu} \hspace{15px} E^{\ce o} = 0.339\: \ce V\)
The reduction potential is a quantity measured by comparison. As mentioned earlier, the reduction potential of the standard hydrogen electrode (SHE) is arbitrarily defined to be zero as a reference point for comparison. When a half cell \(\ce{Cu^2+ || Cu}\) for the reaction
\(\ce{Cu^2+ + 2 e^- \rightarrow Cu}\)
is coupled with the Standard Hydrogen Electrode (SHE), the copper electrode is a cathode, where reduction takes place. The potential across the cell
\(\ce{Pt\, |\, H_{2\: \large{(g,\: 1\: atm)}}\, |\, H+_{\large{(aq)}},\: 1\: M\, ||\, Cu^2+ \, |\, Cu}\)
has been measured to be 0.339 V. This indicates that \(\ce{Cu^2+}\) ions are easier to reduce than the hydrogen ions, and we usually represent it by
\(\ce{Cu^2+ + 2 e^- \rightarrow Cu} \hspace{15px} E^{\ce o} = 0.339\: \ce V\)
A positive cell potential indicates a spontaneous reaction.
When the cell \(\ce{Zn\, |\, Zn^2+}\) is coupled with the SHE,
\(\ce{Zn\, |\, Zn^2+_{\large{(aq)}}\: 1\: M\, ||\, H+_{\large{(aq)}},\: 1\: M\, |\, H_{2\: \large{(g,\: 1\: atm)}}\, |\, Pt}\)
The potential has been measured to be 0.76 V. However, in this cell, \(\ce{Zn}\) is oxidized, and its electrode is the anode. Therefore, the reduction potential has a negative value for the reduction reaction
\(\ce{Zn^2+ + 2 e^- \rightarrow Zn} \hspace{15px} E^{\ce o} = - 0.76\: \ce V\)
This means that \(\ce{Zn^2+}\) ions are less ready to accept electrons than hydrogen ions.
Ideally, for every redox couple, there is a reduction potential. Reduction potentials of standard cells have been measured against the SHE or other standards; their potentials are measured. These values are usually tabulated in handbooks. A short Standard Reduction Potentials table is available from the HandbookMenu, but you may also click the live link to see one.
Questions
- Choose the single correct or the single incorrect statement:
- At the anode, oxidation takes place only when used as a battery.
- At the anode, oxidation takes place in a battery and in an electrolysis operation.
- At the cathode, oxidation takes place only when used as a battery.
- At the cathode, oxidation takes place in a battery and in an electrolysis operation.
- All chemical reactions that supply the power to a battery are oxidation reduction reactions. True or false?
- The half-cell using the reaction:
\(\mathrm{2 H^+_{\large{(aq,\: 1.00\: F)}} + 2 e^- \rightarrow H_{2\:\large{(g,\: 1\:atm)}}}\)
has a half cell potential of zero because- it is so defined.
- hydrogen is not very reactive.
- its potential is absolutely zero.
- it is not a useful electrode.
- The notation to indicate a boundary between two phases in an electrochemical cell is
- |
- /
- ||
- \
- The notation to indicate a salt bridge between two half electrochemical cells is
- |
- /
- ||
- \
Solutions
- Answer... B.
Consider...
It is a convention to call the reduction electrode a cathode in a battery or in an electrolysis operation. The oxidation reaction occurs at the anode. - Answer... True!
Consider...
Only RedOx reactions involve electron transfer. Even concentration cells involve oxidation and reduction of the same material. Note that \(\ce{Ag+ + Cl- \rightarrow AgCl_{\large{(s)}}}\) is an ionic reaction, not a redox reaction. -
Answer... A.
Consider...
No cell potential is ABSOLUTELY zero. \(\ce{H2}\) is reactive. This is not the reason at all. -
Answer... A.
Consider...
The vertical bar | is used to indicate a boundary between two phases.
\(\ce{Pt\, |\, H2\, |\, H+}\: (1.0\: \ce M)\) represents the hydrogen half cell. -
Answer... C.
Consider...
Only | and || are used among the four notations. Two vertical bars, ||, represent a salt bridge.
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)

