3: Mass Transport Mechanisms
- Page ID
- 61293
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The faradaic current that flows at any time is a direct measure of the rate of the electrochemical reaction taking place at the electrode. Further, the current itself is dependent upon two things:
- the rate at which material gets from the bulk of solution to the electrode, known as mass transport, and
- the rate at which electrons can transfer across the interface, or charge transfer kinetics.
These two processes are inexorably intertwined in the flow of current.
There are three basic mechanisms of mass transport:
- Diffusion – defined as the spontaneous movement of any material from where it is to where it is not
- Migration – the movement of charged particles in an electric field
- Convection – movement of material contained within a volume element of stirred (hydrodynamic) solution
Diffusion
The random movement of molecules from a region of high concentration to regions of lower concentration, shown in Figure 7 for one dimension, is called diffusion. The rate at which a molecule diffuses is dependent upon the difference in concentration between two points in solution, called the concentration gradient, and on the diffusion coefficient, \(D\), which has a characteristic value for a specific solution species at fixed temperature.
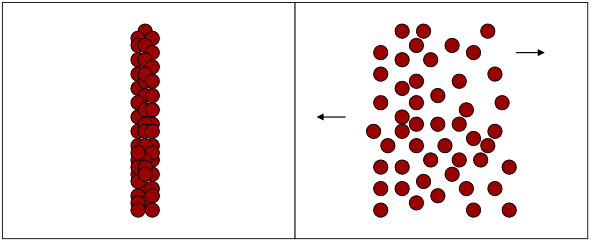
Figure 7
This movement of a chemical species under the influence of a concentration gradient is described by Fick’s first law. A particle i will diffuse through a cross-sectional area as a function of the concentration gradient across the selected area. Flux, as particles per unit time across the given segment, is expressed as Ji according to
\[J_i = -D_i \dfrac{∂C_i}{∂x}\]
where \(∂C_i / ∂x\) expresses the concentration gradient and \(D_i\) the diffusion coefficient for particle \(i\).
Migration
The movement of charged particles in response to a local electric field is called migration. The contribution of migration to the total flux is proportional to the charge of the ion, the ion concentration, the diffusion coefficient, and the magnitude of the electric field gradient experienced by the ion. A change in the applied potential to a solid electrode in a solution containing ions affects charge migration as illustrated in Figure 8 for increasing negative charge at the electrode surface.
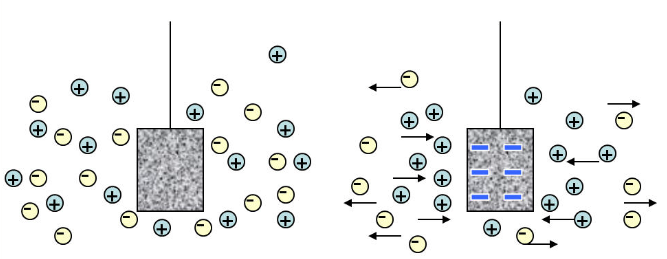
Figure 8
Convection
The movement of fluids is described by hydrodynamics. Convection as it applies to electrochemistry is forced movement of solution species by mechanical (stirring) or other means. The rate at which a solution is stirred can generally be controlled, with the convective contribution (in one dimension) to total flux of a species described in terms of its hydrodynamic velocity, νx. The effect of stirring a solution is shown in Figure 9.
Figure 9
Total Mass Transport
The total mass transport of material, or flux, to an electrode is described for one dimension by the Nernst-Planck equation
\[\mathrm{J_{(x,t)} = -[D (∂C_{(x,t)} / ∂x)] - [(zF/ RT)\: D\: C_{(x,t)}](∂φ_{(x,t)} / ∂x) + C_{(x,t)}ν_{x\, (x,t)}}\]
where J is the flux (mol cm-2 s-1), D is the diffusion coefficient of the solution species (cm2/s), C is the concentration of the species (mol/cm3), φ is the electrostatic potential, and νx is the hydrodynamic velocity. The Nernst-Planck equation combines the individual contributions from diffusion (concentration gradient), migration (electric field), and convection (hydrodynamic velocity). This equation shows that the flux of material towards the electrode surface is proportional to either of three slopes of concentration, electrostatic potential, or hydrodynamic velocity, all as a function of distance from the electrode surface.
Electrochemical experiments can be designed to eliminate the contributions of electrostatic potential and hydrodynamic velocity to the overall flux of electroactive species, limiting mass transport to the contribution from diffusion. The currents resulting from these experiments can then be classified as diffusion controlled.
Contributions from migration can be effectively eliminated by adding an inert electrolyte to the solution at a 10 – 100 fold excess with respect to the redox couple of interest. The electric field between the two electrodes involved in the measurement is dissipated over all of the ions in solution and not just the electroactive material. Under these conditions, the contribution of migration to the observed current is < 1%. Contributions from convection can be reduced or eliminated by working in quiet (unstirred) solutions. With careful control of external vibration and temperature, diffusion controlled measurements for up to 20 seconds or so can be made without significant convective effects.
The flux can then be related to the observed current at the working electrode by
\[\mathrm{i_t = n\, F\, A\, D\, (∂C_i / ∂x) │_{x = 0}}\]
where A is the electrode area (cm2), and other symbols have their previous meaning. We will investigate this relationship further in the next section.


