Analysis of Anions by Spectrophotometry
- Page ID
- 220914
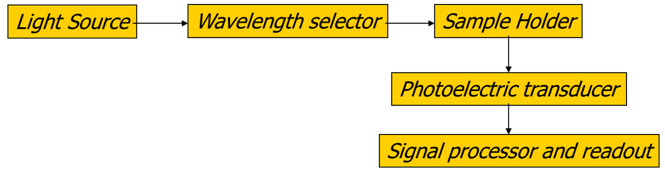
Q1: Draw a block diagram of the components of a spectrophotometer.
A simple diagram may look like:
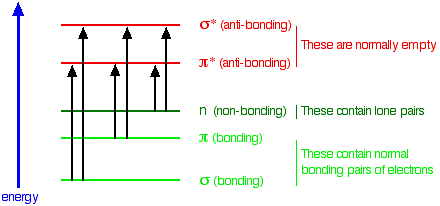
Q2: What molecular properties must a compound have in order to absorb UV-VIS radiation?
The compound must have electrons that absorb light in the UV-VIS range. For example, in organic molecules, this is due to electronic transitions from a bonding or non-bonding orbital to an empty anti-bonding. The following diagram summarizes possible absorption transitions.
Q3: Do you think phosphate ions have the ability to absorb UV or visible radiation? Justify your answer.
Phosphate might be able to absorb light in the UV or visible range but this transition may not be very specific and therefore may not be useful for analytical determinations.
The next activity can be performed in lab using a spectrophotometer and solutions of red and blue dyes or can be simulated using the simulator at the following website http://web.mst.edu/~gbert/ColorScan/Spectrophotometry.HTML
Prepare solutions of red dye and blue dye and record their spectra between 400 and 700 nm.
- The blue dye has a maximum absorption peak at approximately 630 nm.
- At which wavelength does the red dye absorb the most?
The red dye has a maximum absorption peak at approximately 520 nm.
- What is the value of the transmittance at λmax for each dye? What is the value of the absorbance?
The blue dye has an absorbance at λmax of approximately 0.88 and 13% transmittance.
The red dye has an absorbance at λmax of approximately 1.0 and 10% transmittance.
- What wavelength would you choose to quantitatively determine the concentration of the red dye? Why did you choose this wavelength?
Since one wants to achieve the best sensitivity for the analysis, λmax is the best choice. For quantitative determinations of the red dye, one would want to tune the spectrophotometer to 520 nm.
- What wavelength would you choose to quantitatively determine the concentration of blue dye? Why did you choose this wavelength?
For the same reason explained above, one would want to work at 630 nm to determine the concentration of blue dye.
Q4: Is it possible to determine the concentration of the blue dye if it is contaminated with some of the red dye?
When observing the absorption spectrum of the red dye, one can see that its absorbance at 630 nm is basically zero. Therefore, it is possible to determine the concentration of blue dye in presence of red dye because there is not an overlap of the two absorptions at λmax . Beer’s law allows to calculate simultaneously the concentration of multiple analytes as long as the contribution from one component to the absorbance at the analytical wavelength of the other component is known and accounted for.
Q5: When does it become possible to selectively measure the blue dye in presence of the red dye?
When the contribution to the absorbance by the red dye at 630 nm is very small.
Q6: Draw a representative plot of A versus c if the spectrophotometer is set to λmax.
A general plot of Absorbance vs. Concentration (expressed in parts per million) will look like:
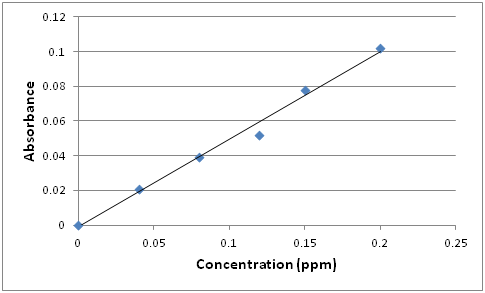
Q7: How could you use this plot to determine the concentration of an unknown?
The best fit line through the experimental points provides a calibration equation y = 0.5054x + 0.001. The concentration of any unknown can be calculated by measuring its absorbance and plugging the value in the calibrating equation and solving for the concentration (x). For example, if the absorbance of the unknown is 0.0663, the concentration would be:
\[x= \dfrac{0.0663-0.001}{0.5054}=0.21\: ppm\nonumber\]
Q8: What wavelength would you choose to quantitatively determine orthophosphate by the molybdenum blue method?
Looking at the absorbance spectrum, the maximum absorbance peak is between 850 and 900 nm. More specifically, a wavelength around 880 nm seems the most appropriate choice.
Q9: What potential interferences would limit the measurement of orthophosphate using the molybdenum blue method?
If there were other species that absorbed at the same wavelength, they would create an interference. However, the sample would appear blue so one would know right away that the method would not be appropriate. Another possible interference could be caused by components in the sample that would react with either ascorbic acid or ammonium paramolybdate, thus preventing the formation of the “molybdenum blue” complex.
Q10: What steps could you take in the sample preparation to decrease the chances of interfering species in the orthophosphate analysis?
If the sample was blue colored to begin with, the method could not be applied unless the blue interferent were removed by some extraction procedure. Cleaning the glassware, such as acid washing, ensure that contaminations are minimized. Other possible interferences such as suspended solids or debris that can compromise the analysis can be removed by filtration.
Q11: Looking at the interferences listed in EPA method 365.1 will any of these affect the way you will analyze your sample for orthophosphate?
According to EPA method 365.1 a potential interferent to the analysis of phosphate is iron in large concentrations. Iron can precipitate phosphate causing loss of analyte. Arsenates are also determined similarly to phosphorus and should be considered when present in concentrations higher than phosphorus. Sample turbidity should be removed by filtration prior to analysis. Any sample color in the same range as that produced by the “molybdenum blue” complex will interfere with the analysis.
Q12: Given that a stock solution of 3 mg/L phosphate (PO43-) is equivalent to a concentration of 1 mg/L of elemental phosphorous (P), how many milliliters will you have to pipette to prepare 25.00 mL of the following six standards?
Since a 0.04 mg/L concentration in elemental P is equivalent to a 0.12 mg/L PO43- we would need:
\[3\: mg/L * x=0.12\: mg/L * 25.00\: mL\nonumber\]
\[x= \dfrac{0.12\: mg/L * 25.00\: mL}{3\: mg/L}=1\: mL\nonumber\]
Similar calculations can be made to determine the volume of stock solution needed to prepare each standard. The table below provides the calculated amounts.
|
Standard concentration (mg P/L) |
Milliliters of phosphate standard to pipette |
|---|---|
|
0.00 |
0 |
|
0.04 |
1 |
|
0.08 |
2 |
|
0.12 |
3 |
|
0.15 |
3.75 |
|
0.20 |
5 |
Q13: What is the purpose of preparing the standard at 0.00 mg/L P? How is it used in the analysis?
The 0.00 mg/L standard is used as the blank in the analysis to zero the response of the spectrophotometer.
Q14: The second standard is 0.04 mg P/L. How many parts per million (ppm) of P does this correspond to?
For dilute solutions mg/L is the same as parts per million. Therefore a 0.04 mg P/L is the same as a 0.04 ppm P solution.
Q15: What relationship do you observe between absorbance and concentration?
The standard calibration curve looks like:
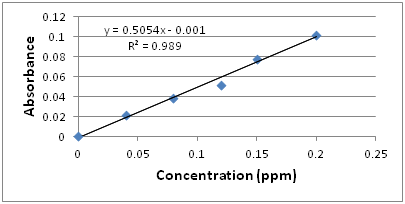
A linear relationship between absorbance and concentration can be observed.
Q16: What parameter allows us to determine whether there is a good fit between absorbance and phosphate concentration?
The correlation coefficient, R2. The closer the value to 1, the better the fit.
Q17: What is the average concentration of phosphate (expressed in mg P/L) in the pond water?
In order to calculate the average concentration of phosphate in the pond water, we need to use the calibration equation, y = 0.5054x – 0.001
For an absorbance of 0.025
\[0.025=0.5054\: x-0.001\nonumber\]
\[x= \dfrac{0.025+0.001}{0.5054}=0.051\: mg\: P/L\nonumber\]
For an absorbance of 0.027
\[0.027=0.5054\: x-0.001\nonumber\]
\[x= \dfrac{0.027+0.001}{0.5054}=0.055\: mg\: P/L\nonumber\]
For an absorbance of 0.023
\[0.023=0.5054\: x-0.001\nonumber\]
\[x= \dfrac{0.023+0.001}{0.5054}=0.047\: mg\: P/L\nonumber\]
The average of the measurement is 0.051 mg P/L
Q18: What parameter allows you to assess if the measurement above is reproducible?
The standard deviation is a measure of the reproducibility of the measurement. In the case outlined above, the standard deviation is ±0.004. A small standard deviation indicates that the result is reproducible.
Q19: How would do determine the average signal and the associated standard deviation of the method blank using the UV-VIS spectrophotometer?
A blank can be prepared that contains all reagents except for the analyte (in this case phosphate). The blank is scanned multiple times (typically 30 or above) and the average and standard deviation of all the scans is calculated.
Q20: If you determined that the average signal from the method’s blank is 0.0081 and the standard deviation is 0.0017, what is the minimum distinguishable analytical signal of the method? What is the detection limit?
The minimum distinguishable analytical signal can be calculated from the average method’s blank and its standard deviation:
\[\mathrm{(S)_{DL} = S_{mb} + 3s_{mb}}\nonumber\]
From here, the limit of detection c DL can be estimated:
\[c_{DL}= \dfrac{S_{DL}-S_{mb}}{m}\nonumber\]
In the particular case, (S)DL = 0.0081 + 3(0.0017) = 0.0132
If the calibration equation is y = 0.5054x – 0.001,
\[c_{DL}= \dfrac{0.0132-0.0081}{0.5054}=0.01\: ppm\nonumber\]
Q21: Would you be able to detect phosphate in the pond water mentioned above if the absorbance of an unknown sample was 0.003?
No, it would not be possible to detect phosphate in a water sample with an absorbance of 0.003 since it falls below the minimum distinguishable analytical signal.
Q22: What are the likely advantages of automating a method?
An automated sampling method would allow a person to process many samples rapidly and with good reproducibility.


