Analysis of Cations by Atomic Spectroscopy
- Page ID
- 219076
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Purpose: The purpose of this module is to introduce fundamental concepts of atomic spectroscopy, particularly flame atomic absorption spectroscopy (FAAS) as it pertains to the measurement of analytes in water samples. Calcium and magnesium are used as specific examples.
Learning Outcomes:
At the end of this assignment, students will be able to:
- Understand the basic operation of a flame absorption spectrophotometer.
- Select the appropriate lamp and wavelength to use for an analysis.
- Evaluate the selectivity of the technique.
- Investigate the quantitative aspects of flame atomic absorption spectrophotometry (e.g., use Beer’s law to calibrate the spectrophotometer and determine the concentration of an unknown amount of calcium and magnesium in a water sample).
For a discussion of fundamental concepts of atomic spectroscopy check the following links:
- Analytical Chemistry 2.0 – Chapter 10
- Heavy Metals in Lake Nakuru – Atomic Spectroscopy
- Atomic Absorption Spectroscopy Learning Module
One common way to analyze for the presence of metal cations in aqueous samples at very low concentrations (parts per million or lower) is by flame atomic absorption spectrophotometry. An atomic absorption (AA) spectrophotometer is similar in many respects to a UV-VIS spectrophotometer except that the lamp needs to be specific to the analyte and the analyte needs to be converted to free atoms (atomization). This last requirement is accomplished by aspirating the sample into a flame that converts metal species to their elemental form. Once in the gas phase, atoms absorb radiation emitted by a special lamp (hollow cathode lamp) chosen to emit the same wavelength that the analyte will absorb. By constructing a standard calibration curve using known concentrations of the analyte under investigation, a relationship can be developed between the absorbance of the analyte at the specific wavelength and its concentration. By measuring the absorbance of an unknown sample, the concentration of the analyte in the sample can be determined.
Q1: Based on the description above, draw a block diagram and label the parts of a flame atomic absorption spectrophotometer.
Each element is characterized by the unique way its electrons are arranged in orbitals around the nucleus - its electronic configuration. These atomic orbitals are designated by type and energy as 1s, 2s, 2p, 3s, 3p, 4s, 3d, etc.
Q2: Write the electron configuration for calcium (Ca, element number 20). In what atomic orbital do the electrons with the most energy reside?
The electron configuration you wrote for the calcium atom describes the element in its lowest energy or ground state.
Q3: Calcium atoms undergo atomic absorption in the flame of the AA. Which electrons absorb the energy from the source?
Q4: Identify some possible absorption transitions for calcium.
Each atomic orbital of an element has a single discrete or quantized amount of energy. Therefore, the energies separating any two atomic orbitals is also discrete or quantized value. Only when the energy of radiation interacting with an atom exactly matches the energy gap between two levels of the atom will an absorption event occur. Because elements have different numbers of electrons, these energy differences are unique to each and can be used to identify that element. Because the energy differences between atomic levels are so specific, meaning that the absorption occurs at a very specific wavelength, the spectra are said to consist of a series of lines.
The energy necessary for a transition can be calculated using the equation:
\[\mathrm{\Delta E = h\nu}\nonumber\]
where ΔE represents the difference in energy between the ground and excited state, h is Planck's constant (h = 6.626 × 10-34 J s), and ν is the frequency of the absorbed radiation.
Q5: Given that the energy difference between the ground state and the first excited electronic state (ΔE) for the calcium atom is 4.687 × 10-19 J, calculate the frequency, ν, corresponding to a photon possessing this energy. Next, calculate the wavelength (in nm) for this photon.
As previously mentioned, for a sample to be analyzed by atomic spectroscopy, it must be in the gas phase. This is accomplished using an atomizer, the most common of which involves a flame, plasma or graphite furnace. Plasmas and graphite furnaces are typically used in analyses requiring the determination of metals at the parts per billion (ppb) level. However, in most water samples, the concentrations of cations such as Ca2+ and Mg2+ are in the parts per million (ppm) range, which are easily attainable by flame AA.
A variety of fuels and oxidants can be used to produce the flame, with the choice dependent upon the desired temperature, which in turn is dependent upon the atom under consideration. Routine analysis of calcium and magnesium can be accomplished with an acetylene/air flame which has a temperature of approximately 2500 K. A “slot” burner, as shown below, is common.
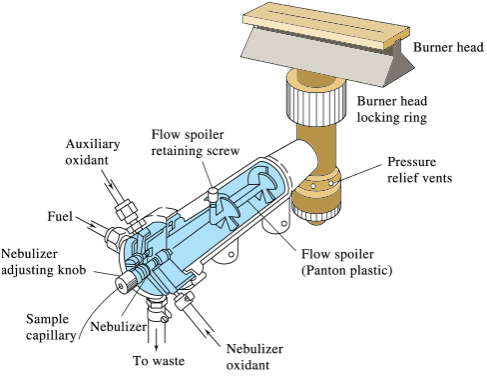
Q6: Why do you think a “slot” burner is used instead of the configuration of a traditional Bunsen burner?
The most common radiation source for flame atomic absorption is the hollow cathode lamp (HCL), which is illustrated below. The hollow cathode is coated with the element of interest, which in our example is calcium. The lamp is filled with a low pressure of argon gas. Argon atoms are ionized to Ar+ at the anode and these ions flow to the cathode. When they strike the cathode, they sputter off calcium atoms into the gas phase. Some of the gas phase calcium atoms are promoted to excited states in the sputtering process. These excited state atoms can emit radiation at specific lines of the element.
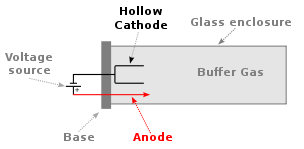
Q7: Do calcium and magnesium absorb at the same wavelength?
Q8: How will this affect the ability to determine both metals simultaneously?
Exploring fundamental relationships in spectrophotometric methods
Much like in UV-VIS spectrophotometry, the amount of radiation absorbed by the atoms of a given analyte in the gas phase is measured by the absorbance, which is defined as
\[\mathrm{A = \log P_0/P}\nonumber\]
where P0 represents the radiant power of the beam before the sample and P after the sample. The absorbance is proportional to the concentration of the analyte according to Beer’s law:
\[\mathrm{A = \varepsilon bc}\nonumber\]
where
A is the absorbance
ε is the molar absorptivity – include that this is a measure of the probability of the transition – the molar absorptivity is largest at λmax, meaning that this is the most probable transition
b is the path length (in this case the length of the burner)
c is the concentration
Q9: How would this type of relationship help you in determining the concentration of Ca2+ and Mg2+ in an unknown water sample?
Analyzing Ca2+ and Mg2+ in water samples
Now that we have developed general background information on flame atomic absorption spectrophotometry, we can explore specific features of its use in the analysis of Ca2+ and Mg2+ in water. You may want to research EPA methods 7140 for analysis of calcium and 7450 for analysis of magnesium.
Q10: What wavelength would you use to measure Ca2+? What wavelength would you use to measure Mg2+?
Q11: If you wanted to measure Mg2+ concentrations, what instrumental parameters would you need to know?
Q12: If you know that the concentration of calcium and magnesium in your water sample is approximately 5 to 10 ppm, suggest a strategy to appropriately calibrate the spectrophotometer for such an analysis.
Q13: If the absorbance of an unknown water sample is found to be greater than the absorbance of the highest calcium standard used to calibrate the spectrophotometer, what steps would you take to ensure that the analysis is providing accurate results?
Q14: Considering that the sample is introduced into the flame through a very thin capillary, what step would you have to take before analyzing a surface water sample that may have small amounts of detritus?
References
- Method 7140 – Calcium AA – Direct Aspiration. Environmental Protection Agency, Washington DC, 1986.
- Method 7450 – Magnesium AA – Direct Aspiration. Environmental Protection Agency, Washington DC, 1986.


