pH / Ion Selective Electrodes
- Page ID
- 222358
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Analysis of cations and anions by Ion-Selective Electrodes (ISEs)
Purpose: The purpose of this assignment is to introduce potentiometric measurements of ionic species by ion selective electrodes (ISEs)
Learning Outcomes: Upon completion of this module, students will be able to:
- Identify electrodes and measurement devices used in potentiometry.
- Predict how analyte concentration (or activity) controls the potential of a potentiometric measurement.
- Choose appropriate measurement conditions to minimize interferences.
- Correct for differences in ionic strength among calibration standards and samples.
- Construct an appropriate calibration curve for potentiometric determinations and account for changes in analyte concentration due to sample dilution.
References: Modules on the theory and operation of ISEs may be found in the Analytical Sciences Digital Library (ASDL) collection. The following hyperlinks will direct the reader to some ASDL resources on potentiometry.
- Analytical Sciences Digital Library. Potentiometry: e-learning module. http://community.asdlib.org/activelearningmaterials/analytical-electrochemistry-potentiometry/ (accessed April 3, 2014).
- Harvey, D. Analytical Chemistry 2.0, Chapter 11. http://www.asdlib.org/onlineArticles/ecourseware/Analytical%20Chemistry%202.0/Text_Files.html (accessed April 3, 2014)
The EPA field manual includes practical aspects of field and lab measurements of pH.
- US EPA Field Manual: http://water.usgs.gov/owq/FieldManual/Chapter6/6.4_ver2.0.pdf
Membrane-based ISEs are widely used in the determination of ionic species. Such determinations fall under the category of a direct potentiometric measurement, which you have experienced if you have ever made a pH measurement. A typical direct potentiometric measurement requires the use of an indicator electrode, a reference electrode, and a high-impedance voltmeter. An example of equipment needed to perform a potentiometric determination is shown in Figure 1.

Figure 1. An experimental setup for the direct potentiometric measurement of sodium ion in aqueous solution.
The two electrodes pictured in Figure 1 represent an electrochemical cell. The electrode on the right is the sodium indicator electrode (sodium ISE). The electrode on the left is a reference electrode. The sodium ISE has a glass membrane that responds specifically to sodium ions. This glass membrane physically separates two solutions: one inside the electrode with a constant sodium ion concentration; one outside the membrane that is the solution you are analyzing. The electrical potential difference generated by the indicator electrode depends on the sodium concentration of the outer solution. Therefore, the function of the indicator electrode is to respond to changes in the analyte concentration in a predictable manner.
The reference electrode provides a known and stable potential to compare against the indicator electrode potential. An assumption when using an ISE system is that the potential of the reference electrode is independent of the concentration of the analyte and matrix of the sample being analyzed. The electrical potential is displayed on the high-impedance voltmeter. The voltmeter has a high impedance to minimize current flow, which prevents changes to the chemical composition of the reference electrode and to the sample (so, for example, if measuring the concentration of H+ with a pH meter, there will not be any reduction of the H+ to hydrogen gas). High impedance, which typically is greater than 1012 ohms, is also needed to minimize errors in the measured potential.
One of the most common examples of ion selective electrodes is a pH electrode – pH electrodes are selective toward the H+ ion. We will start our exploration of ISEs by understanding how a pH electrode works. pH electrodes also use a glass membrane (this membrane is about 0.1 mm thick, so is quite fragile), but in this case it is a type of glass more sensitive toward the H+ ion instead of the Na+ ion. The internal solution has a fixed and known concentration of H+. The external solution is the sample whose pH you wish to measure. The concentration of H+ in the external solution varies depending on the sample being analyzed. An important point is that the glass used to manufacture the membrane has some sodium ions (Na+) in it. A key factor in the functioning of the membrane is that the inner and outer surfaces of the glass form a very thin hydrated gel layer when in contact with water (Figure 2). The internal and external hydrated gel layers are only about 10 nm thick, which is much less than the 0.1 mm thickness of the glass membrane, so a layer of dry glass always separates the two hydrated gel layers. Cations from the solution have the ability to migrate into the hydrated gel layer. For a pH electrode, that means that H+ ions from the solution will displace some of the Na+ ions in the glass that makes up the hydrated gel layer.
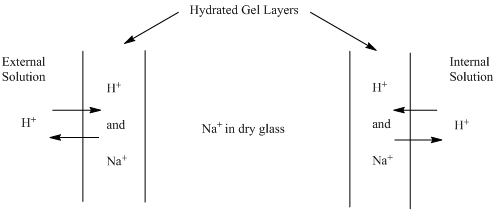
Figure 2. Representation of the glass membrane in a pH electrode. Note: the width of the hydrated gel layers in the representation is too large relative to the width of the dry glass portion of the membrane.
Many of you may have used a pH electrode before. If you did, it likely appeared to consist of only a single electrode. In actuality, it is a two-electrode system, but it is designed in such a way that the reference electrode is incorporated into the glass membrane electrode. The design of the combination-electrode system incorporates an electrical contact between the reference and indicator electrode that is necessary to complete the electrical circuitry and produce a potential reading.
Q1: Will a more acidic sample displace more, the same or less Na+ from the hydrated gel layer?
Different concentrations of H+ and Na+ in the hydrated gel layer cause different junction potentials. Note that the junction potential at the interface of the membrane with the internal solution never changes because the concentration of H+ is constant in the internal solution. The junction potential at the interface of the membrane with the outer solution changes for different samples with different pH. The specific reason why varying concentrations of H+ and Na+ can be found in the outer gel layer has to do with something called the mobility of the ions.
Q2: What do you think is meant by mobility of ions?
Q3: Which ion do you think has a higher mobility, H+ or Na+?
As mentioned earlier, a reference electrode is used because its junction potential stays fixed no matter what the external solution. Therefore, the only junction potential in the entire circuit of an ion selective electrode that changes is the one at the interface of the ion selective membrane and the external (sample) solution. In the case of a Na+ ion selective electrode a glass membrane of a different composition than the glass membrane in a pH electrode is used– namely one that is more responsive to sodium ions migrating into the glass. Other ion selective electrodes can be fabricated provided a membrane exists that is selective toward the ion one wishes to measure.
Q4: Do you think other cations (e.g., Li+. K+) may have some ability to migrate into the hydrated gel layer of a pH electrode? If so, is this a problem?
The potential measured by the voltmeter is described by Equation \(\ref{1}\).
\[\mathrm{E_{cell} = E_{ind} - E_{ref} + E_{lj}} \label{1} \]
In eq \(\ref{1}\), Ecell represents the potential of the electrochemical cell, Eind represents the half-cell potential of the indicator electrode, Eref represents the half-cell potential of the reference electrode, and Elj represents the liquid-junction potential between the sample solution and the outside membrane of the indicator electrode.
Of particular interest is the relationship between Ecell and the concentration of the analyte. Remember, Ecell is measured but there is only one junction potential (Elj) in the entire system that changes (at the frit), so a measurement of Ecell is essentially a measure of the one varying junction potential.
For the Na+ ion selective electrode, the varying junction potential only depends on the concentration of Na+. However, the situation is more complicated than just using the concentration of Na+, because ion-selective electrode measurements are most commonly performed in solutions with ionic strengths that are greater than zero. In these solutions, there is a difference between the formal concentration (i.e. how the solution was prepared in the lab) and the effective concentration or activity of the analyte.
Q5: Consider a solution that has some Na+ and very high concentrations of K+Cl-. What effect do you think this might have on the activity of Na+ in the solution?
The relationship between activity and concentration for sodium is illustrated in Equation \(\ref{2}\).
\[\mathrm{a_{Na}= γ_{Na} [Na^+]} \label{2} \]
In eq \(\ref{2}\), aNa is the sodium ion activity (mol L-1) , [Na+] is the sodium ion concentration (mol L-1), and γNa is the activity coefficient for the sodium ion. As we just discussed, as the sample ionic strength increases, there is a greater probability that analyte ions will interact with oppositely charged ions from the supporting electrolyte(s) dissolved in the sample. This effectively decreases the concentration of the “free ion”, which is represented by a decrease in the activity coefficient. As the ionic strength of a solution approaches zero, the activity coefficient approaches one, and under infinitely dilute conditions, the analyte activity and analyte concentration are equal. The relationship between the oxidized and reduced forms of sodium written as a reduction reaction can be described in Equation \(\ref{3}\).
\[\ce{Na+ (aq) + e- → Na (s)} \label{3} \]
The half-cell potential of the indicator electrode responds to changes in the activity of the analyte as described by the generalized form of the Nernst equation in Equation \(\ref{4}\):
\[\mathrm{E_{ind}= E_{ind}^o- \dfrac{RT}{nF} \ln\left(\dfrac{1}{a_{Na}} \right)} \label{4} \]
In eq \(\ref{4}\), E° is the indicator electrode potential under standard conditions (298 K, 1.00 M Na+), R is the molar gas constant (8.314 J K-1 mol-1) , T is the absolute temperature (K) , n is the number of moles of electrons in the half-reaction, and F is Faraday’s constant (96485 C mol-1).
Q6: If the indicator electrode potential under standard conditions is -0.100 V, what is the indicator electrode potential at 298 K if the activity of the sodium ion is 0.10 M?
Q7: How does the indicator electrode potential change in the previous question if the temperature is increased by 10 degrees?
A sodium ion selective electrode must be calibrated before it can be used to measure the concentration of Na+ in an unknown sample.
Q8: How would you go about calibrating a sodium ion selective electrode?
We just discussed how the ionic strength of a solution impacts the activity of Na+. Suppose you wanted to analyze the sodium concentration of a low ionic strength sample such as natural pond water.
Q9: Can you think of a way to mitigate possible effects of ionic strength to insure that your calibration procedure and sample analysis provide an accurate measurement of the concentration of Na+ in the unknown?
If one keeps the ionic strength high and constant, then the Nernst equation can be expressed in terms of analyte concentrations (and not activities) because the activity coefficient of all samples and standards are equivalent and knowledge of activity is no longer critical.
Q10: Would this proposed way to mitigate possible effects of ionic strength be utilized in pH measurements?
Q11: In the potentiometric determination of sodium ion of a mineral water sample, indicate if either of the following supporting electrolytes can be used for ionic strength adjustment: a 4.0M NH3 – NH4Cl buffer (pH 10) or 4.0M NaCl.
Q12: What would be the general criteria you would need to use in selecting a suitable supporting electrolyte for an analysis using an ion selective electrode?
The concentration of each calibration standard can be expressed as a formal concentration. The concentration term in the Nernst equation is often converted from base e to base 10, which can also be expressed as a p-function, shown in Equation \(\ref{5}\).
\[\mathrm{pNa= - \log[Na^+]} \label{5} \]
Assuming a temperature of 298 K, and the constants R, T and F combined into a single value, under those conditions, the Nernst equation takes on the following form for cationic analytes (shown for sodium in Equation \(\ref{6}\)):
\[\mathrm{E_{cell}= E_{cell}^o- \dfrac{0.05915}{n} pNa} \label{6} \]
Q13: Based on the relationship in eq \(\ref{6}\), how would you construct a calibration that links the changes in electrode potential to changes in the concentration of the sodium ion?
Q14: What is the expected slope of a potentiometric calibration curve for sodium at 35°C? What effect does temperature have on the slope of a potentiometric calibration curve?
As discussed earlier, indicator electrodes do not have a specific response to a given analyte, but have a wide range of responses to a group of analytes that are similar in charge and size. The electrode is designed to exhibit the greatest response for the target analyte, but the presence of chemically similar analytes in a sample may interfere with the determination of the target analyte and bias the potentiometric response. The selectivity of an ion-selective electrode is expressed by Equation \(\ref{7}\)
\[\mathrm{E_{ind}=E_{ind}^o- \dfrac{0.05915}{n_{Analyte}} \log\{a_{Analyte}+ K_{Analyte,Interferent} (a_{Interferent} )^{n_{Analyte}⁄n_{Interferent} } \} } \label{7} \]
Expressed in Equation \(\ref{8}\), the selectivity coefficient \(\mathrm{(K_{Analyte,Interferent})}\) is a ratio of analyte to interferent activities where each species influences the indicator electrode potential to the same degree.
\[\mathrm{K_{Analyte,Interferent}=\dfrac{a_{Analyte}}{(a_{Interferent} )^{n_{Analyte}⁄n_{Interferent} }}} \label{8} \]
Q15: If a sample has a sodium concentration of 1.0 x 10-3 M, and the sodium ISE has a selectivity coefficient of KNa,H = 30, what sample pH would cause a 1% error in the sodium ISE response?
Q16: Evaluate whether it is best to use alkaline or acidic conditions to determine the sodium ion concentration by ISE?
Whenever a method calibration is performed using linear regression (i.e. a best-fit line or trendline, as it is called in Microsoft Excel), it is understood that extrapolating beyond the concentration range used in the regression analysis can lead to biased results. Typically when the analyte concentration in a sample is greater than the analyte concentration for the most concentrated standard, the sample is diluted so that the analyte concentration is between the lowest and highest standard on the calibration curve. The original sample concentration is calculated using the dilution equation, shown in eq \(\ref{9}\).
\[C_1 V_1= C_2 V_2 \label{9} \]
In eq \(\ref{9}\), C1 is the analyte concentration of the original (undiluted) sample, V1 is the volume of the original sample, V2 is the volume of the diluted sample, and C2 is the analyte concentration of the diluted sample. If the sample is diluted prior to analysis, the response of the diluted sample is used as the y-value in the calibration equation and the analyte concentration of the diluted sample is the x-value determined using the calibration equation. The analyte concentration of the original sample is calculated using the dilution equation.
Q17: The table below contains sodium ISE calibration data. If the cell potential measured in a sample is ‑0.115 V, determine the sodium concentration (mol L-1) in this sample.
|
[Na+] (M) |
Ecell (V vs SCE) |
|---|---|
|
1.0 x 10-4 |
-0.221 |
|
1.0 x 10-3 |
-0.164 |
|
1.0 x 10-2 |
-0.107 |
|
1.0 x 10-1 |
-0.048 |
Q18: In the previous question, the sample was prepared by pipetting 5.00 mL of the original water sample and 2.00 mL of an ionic strength adjustment buffer into a 100 mL volumetric flask and diluting to the mark with distilled water. Determine the sodium concentration (mol L-1) in the original water sample.


