4.2: Working With Binary Numbers

In Chapter 7 we will examine several transducers for counting photons. The transducers are made of an array—some use a linear array and some use a two-dimensional array—of individual detecting units. We will worry about the details of how these transducers work in Chapter 7, but if you take a quick look at Figure 7.5.4 – 7.5.6 you will see that the number of individual detecting units are interesting: a linear array of 1024 individual units; another linear array, but with 2048 units, and a two-dimensional array that has \(1024 \times 1024 = 1,048,576\) individual units. What is interesting about these numbers is that each is a power of two: \(1024 = 2^{10}\), \(2048 = 2^{11}\), and \(1,048,576 = 10^{20}\).

Humans are comfortable working with numbers expressed using a decimal notation that relies on 10 unique digits (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9), but computers work with information using a binary notation that is limited to just two unique digits (0 and 1). Although we will not complete calculations using binary numbers, you will see examples of instrumental methods, such as FT-NMR, where the data analysis algorithms (the Fourier transform in this case) require that the number of data points be a power of two. It is useful, therefore, to be familiar with how we represent numbers in both decimal and binary form.

Decimal Representation of Numbers

My university was founded in 1837, which is a decimal expression of the year. Each of these four digits represents a power of 10, a fact that is clear when we read the number out loud: one thousand—eight hundred— thirty—seven, or, when we write it out this way

\[(1 \times 1000) + (8 \times 100) + (3 \times 10) + (7 \times 1) = 1837 \nonumber \]

or this way

\[(1 \times 10^3) + (8 \times 10^2) + (3 \times 10^1) + (7 \times 10^0) = 1837 \nonumber \]

We refer to the 7 being in the ones place (\(10^0 = 1\)), the 3 in the tens place (\(10^1 = 10\)), the 8 in the hundreds place (\(10^2 = 100\)), and the 1 in the thousands place (\(10^3 = 1000\)). Figure \(\PageIndex{1}a\) shows these three ways of representing a number using a decimal notation.

Figure \(\PageIndex{1}\). Three notations used to represent a number using (a) decimal digits and powers of 10 and (b) binary digits and powers of 2. The same number is represented in both (a) and (b).

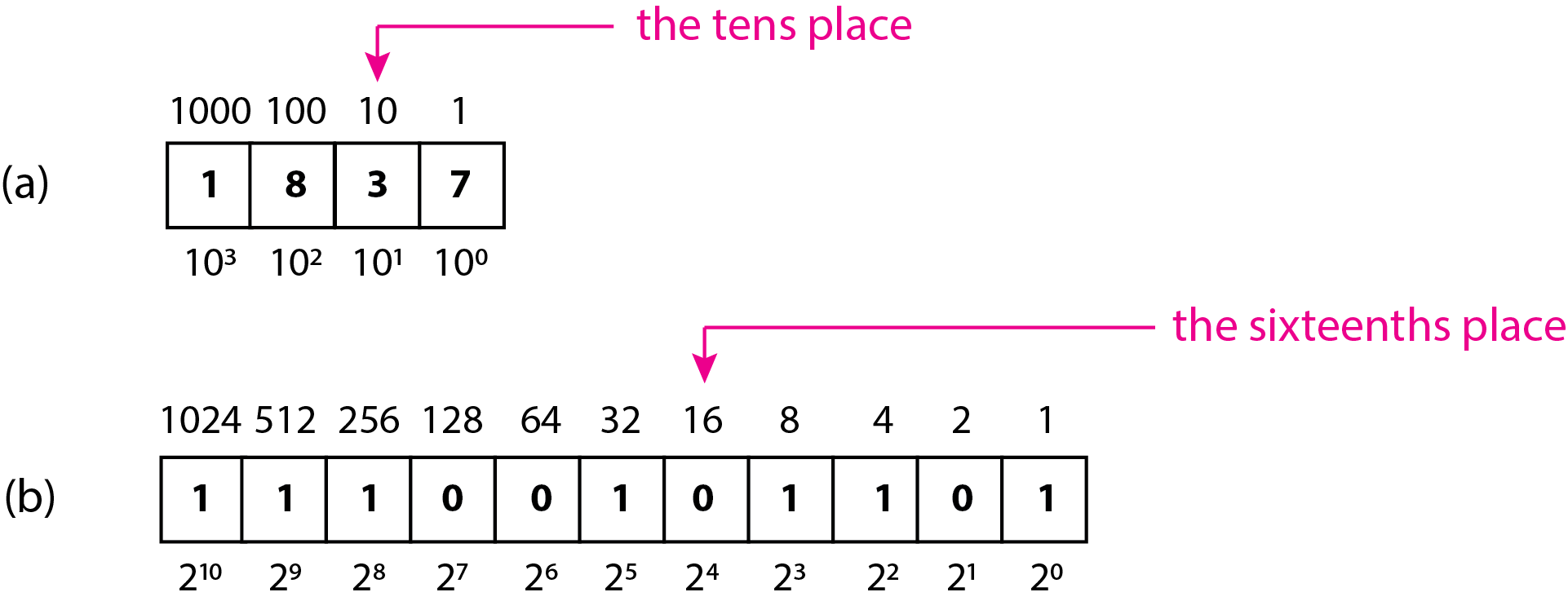
Binary Representation of Numbers

The decimal number 1837 is 11100101101 in binary notation. We can see that this is true if we follow the pattern for decimal numbers in reverse. There are eleven binary digits, so we begin by expressing the number as multiples of the powers of two from \(2^{10}\) to \(2^{0}\), beginning with the digit furthest to the left and moving to the right

\[(1 \times 2^{10}) + (1 \times 2^{9}) + (1 \times 2^{8}) + (0 \times 2^{7}) + (0 \times 2^{6}) + (1 \times 2^{5}) + (0 \times 2^{4}) + (1 \times 2^{3}) + (1 \times 2^{2}) + (0 \times 2^{1}) + (1 \times 2^{0}) = 1837 \nonumber \]

Each power of two has a decimal equivalent—\(2^4\) is the same as \(2 \times 2 \times 2 \times 2 = 16\), for example—which we can express here as

\[(1 \times 1024) + (1 \times 512) + (1 \times 256) + (0 \times 128) + (0 \times 64) + (1 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) = 1837 \nonumber \]

Each power of two represents a place as well; thus, the second 0 from the right is in the sixteenths place. Figure \(\PageIndex{1}b\) provides a visual representation of these ways of expressing a binary number.

Converting Between Decimal and Binary Representations of Numbers

There are lots of on-line calculators that you can use to convert between decimal and binary representations of numbers, such as the one here. Still, it is useful to be comfortable with converting numbers by hand. Converting a binary number into its decimal equivalent is straightforward, as we showed above for the binary representation of the year in which my university was founded

\[11100101101 = (1 \times 1024) + (1 \times 512) + (1 \times 256) + (0 \times 128) + (0 \times 64) + (1 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) = 1837 \nonumber \]

Converting a decimal number, such as 1837, into its binary equivalent requires a bit more work; Table \(\PageIndex{1}\) will help us organize the conversion. We begin by writing the dividend, which is 1837, in the left-most column and divide it by 2, writing the quotient of 918 in the second column and the remainder of 1 in the third column; note that dividing by 2 gives a remainder of 0 if the dividend is even or a remainder of 1 if the dividend is odd. The remainder is the exponent for the first place in the binary notation. In this case, we have \(2^0 = 1\). The quotient becomes the dividend for the next cycle, with the process continuing until we achieve a quotient of 0. The binary equivalent of the original decimal is given by reading the remainders from bottom-to-top as 11100101101.

Table \(\PageIndex{1}\). Converting a binary number into its decimal equivalent.

dividend	quotient	remainder	binary notation
1837	918	1	\(2^0 = 1\)
918	459	0	\(2^1 = 1\)
459	229	1	\(2^2 = 1\)
229	114	1	\(2^3 = 1\)
114	57	0	\(2^4 = 1\)
57	28	1	\(2^5 = 1\)
28	14	0	\(2^6 = 1\)
14	7	0	\(2^7 = 1\)
7	3	1	\(2^8 = 1\)
3	1	1	\(2^9 = 1\)
1	0	1	\(2^{10} = 1\)