1.7: Structural Resolution
- Page ID
- 352426
In the context of this chapter, you will also be invited to visit these sections...
- Crystallization methods for proteins
- Crystal symmetry and diffraction symmetry
- Conditions for systematic absences
- The Patterson function and the Patterson method
- The anomalous dispersion
In previous chapters, we have seen how X-rays interact with periodically structured matter (crystals), and the implicit question that we have raised from these earlier chapters is:
Can we "see" the internal structure of crystals?, or in other words,
Can we "see" the atoms and molecules that build crystals?
The answer is definitely yes!
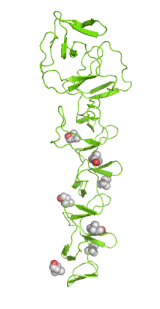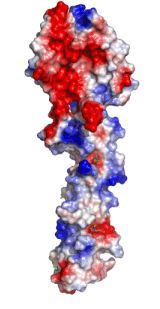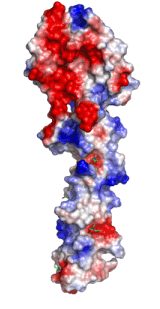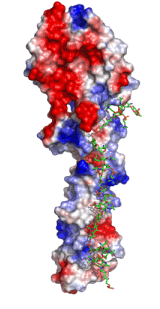

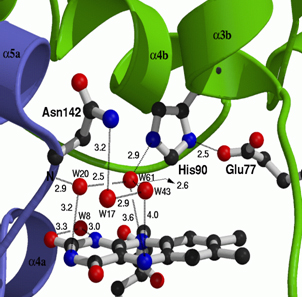
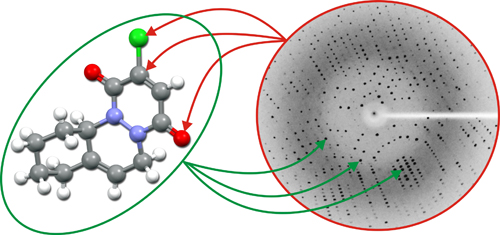
Left: Molecular structure of a pneumococcal surface enzyme
Center: Molecular packing in the crystal of a simple organic compound, showing its crystallographic unit cell
Right: Geometric details showing several molecular interactions in a fragment of the molecular structure of a protein
As the examples above demonstrate, crystallography can show us the structures of very large and complicated molecular structures (left figure) and how molecules pack together in a crystal structure (center figure). We can also see every geometric detail, as well as the different types of interactions, among molecules or parts of them (right figure).
However, for a better understanding of the fundamentals on which this response is based, it is necessary to introduce some new concepts or refresh some of the previously seen ones...
In previous chapters we have seen that crystals represent the organized and ordered matter, consisting of associations of atoms and/or molecules, corresponding to a natural state of it with a minimum of energy.
We also know that crystals can be described by repeating units in the three directions of space, and that this space is known as direct or real space. These repeating units are know as unit cells (which also serve as a reference system to describe the atomic positions). This direct or real space, the same in which we live, can be described by the electron density, ρ(xyz), a function defined in each point of the unit cell of coordinates (xyz), where, in addition, operate symmetry elements which repeat atoms and molecules within the cell.

Unit cell (left) whose three-dimensional stacking builds a crystal (right)

Motifs (atoms, ions or molecules) do repeat themselves by symmetry operators inside the unit cell.
Unit cells are stacked in three dimensions, following the rules of the lattice, building the crystal.
We have also learned that X-rays interact with the electrons of the atoms in the crystals, resulting in a diffraction pattern, also know as reciprocal space, with the properties of a lattice (reciprocal lattice) with a certain symmetry, and where we also can define a repeating cell (reciprocal cell). The "points" of this reciprocal lattice contain the information on the diffraction intensity.


Left: Interaction between two waves scattered by electrons. The resulting waves show areas of darkness (destructive interference), depending on the angle considered. Image originally taken from physics-animations.com.
Right: One of the hundreds of diffraction images of a protein crystal. The black spots on the image are the result of the cooperative scattering (diffraction) from the electrons of all atoms contained in the crystal.
Through this cooperative scattering (diffraction), scattered waves interact with each other, producing a single diffracted beam in each direction of space, so that, depending on the phase differences (advance or delay) among the individual scattered waves, they add or subtract, as shown in the two figures below:
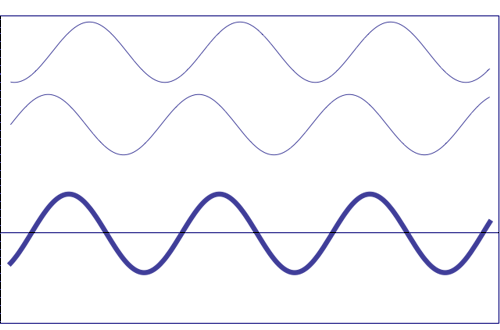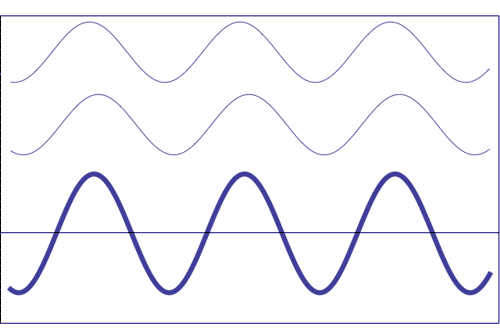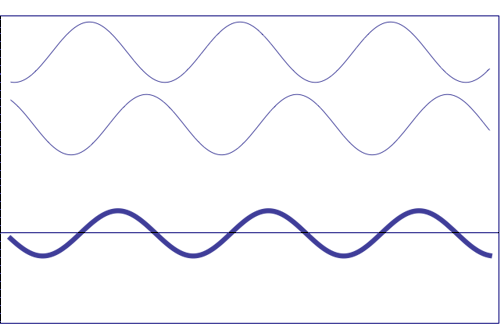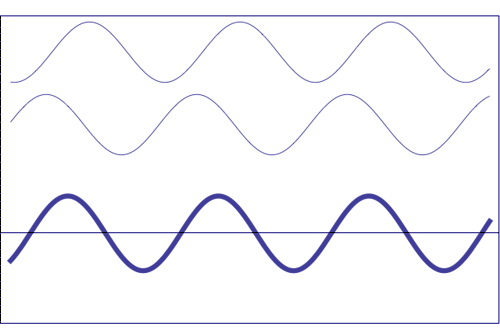
Interference of two waves with the same amplitude and frequency (animation taken from The Pennsylvania State University)

Composition of two scattered waves. A = resultant amplitude; I = resultant intensity (~ A2)
(a) totally in phase (the total effect is the sum of both waves)
(b) with a certain difference of phase (they add, but not totally)
(c) out of phase (the resultant amplitude is zero)
Between the two mentioned spaces (direct and reciprocal) there is a holistic relationship (every detail of one of the spaces affects the whole of the other, and vice versa). Mathematically speaking this relationship is a Fourier transform that cannot directly be solved, since the diffraction experiment does not allow us to know one of the fundamental magnitudes of the equation, the relative phases (Φ) of the diffraction beams.
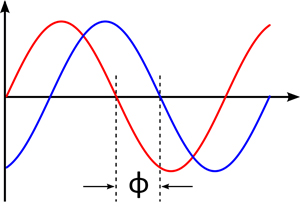
Left: Holistic relationship between direct space (left) and reciprocal space (right). Every detail of the direct space (left) depends on the total information contained in the reciprocal space (right), and vice versa... Every detail of the reciprocal space (right) depends on the total information contained in the direct space (left).
Right: Graphical representation of the out-of-phase between two waves. Relative phase between waves
The diagram below, with the help of the following paragraph, summarizes what the resolution of a crystalline structure through X-ray diffraction implies ...
Atoms, ions, and molecules are packed into units (elemental cells) that are stacked in three dimensions to form a crystal in space that we call direct or real space. The diffraction effects of the crystal can be represented as points of a lattice mathematical space that we call the reciprocal lattice. The diffraction intensities, that is, the blackening of these points of the reciprocal lattice, represent the moduli of some fundamental vector quantities, which we call structure factors. If we get to know not only the moduli of these vectors (the intensities), but their relative orientations (that is, their relative phases), we will be able to obtain the value of the electron density function at each point of the elementary cell, providing thus the positions of the atoms that make up the crystal.

Outline on basic crystallographic concepts: direct and reciprocal spaces. The issue is to obtain information on the left side (direct space) from the diffraction experiment (reciprocal space).
ELECTRON DENSITY
In order to know (or to see) the internal structure of a crystal we have to solve a mathematical function known as the "electron density;" a function that is defined at every point in the unit cell (a basic concept of the crystal structure introduced in another chapter).
The function of electron density, represented by the letter ρ, has to be solved at each point within the unit cell given by the coordinates (x, y, z), referred to the unit cell axes. At those points where this function takes maximum values (estimated in terms of electrons per cubic Angstrom) is where atoms are located. That means that if we are able to calculate this function, we will "see" the atomic structure of the crystal.
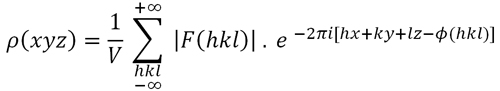
Formula 1. Function defining the electron density in a point of the unit cell given by the coordinates (x, y, z)
- F(hkl) represents the resultant diffracted beams of all atoms contained in the unit cell in a given direction. These magnitudes (actually waves), one for each diffracted beam, are known as structure factors. Their moduli are directly related to the diffracted intensities.
- h, k, l are the Miller indices of the diffracted beams (the reciprocal points) and Φ(hkl) represent the phases of the structure factors. V represents the volume of the unit cell. The function has limitations due to the extent to which the diffraction pattern is observed. The number of observed structure factors is finite, and therefore the synthesis will only be approximate and may show some truncation effects.

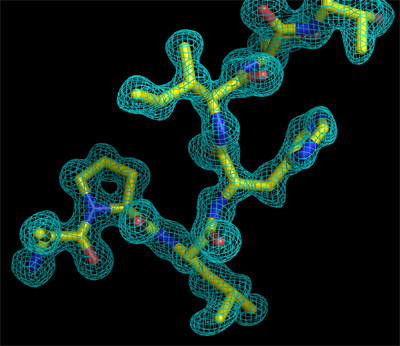
Left: Appearance of a zone of the electron density map of a protein crystal, before it is interpreted.
Right: The same electron density map after its interpretation in terms of a peptidic fragment.
The equation above (Formula 1) represents the Fourier transform between the real or direct space (where the atoms are, represented by the function ρ) and the reciprocal space (the X-ray pattern) represented by the structure factor amplitudes and their phases. Formula 1 also shows the holistic character of diffraction, because in order to calculate the value of the electron density in a single point of coordinates (xyz) it is necessary to use the contributions of all structure factors produced by the crystal diffraction.
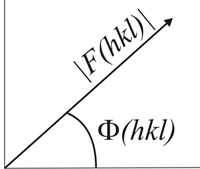
The structure factors F(hkl) are waves and therefore can be represented as vectors by their amplitudes, [F(hkl)], and phases Φ(hkl) measured on a common origin of phases.
When the unit cell is centrosymmetric, for each atom at coordinates (xyz) there is an identical one located at (-x,-y,-z). This implies that Friedel's law holds F(h,k,l) = F(-h,-k,-l) and the expression of the electron density (Formula 1) is simplified, becoming Formula 1.1. And the phases of the structure factors are also simplified, becoming 0° or 180°...
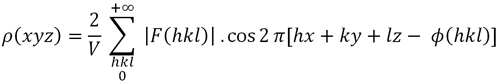
Formula 1.1. Electron density function in a point of coordinates (x, y, z) in a centrosymmetric unit cell.
It is important to realize that the quantity and quality of information provided by the electron density function, ρ, is very dependent on the quantity and quality of the data used in the formula: the structure factors F(hkl) (amplitudes and phases!). We will see later on that the amplitudes of the structure factors are directly obtained from the diffraction experiment.
If your browser is Java enabled, as a practical exercise on Fourier transforms we recommend visiting he following links:
- or, even better, the Java applet kindly provided by Nicholas Schöni y Gervais Chapui (École Polytechnique Fédérale de Lausanne, Switzerland), that you can download (free of any virus) from the link shown and execute in your own computer. This applet calculates the Fourier transform of a two dimensional density function ρ(x) yielding the complex magnitude G(S), the reciprocal space. The applet is also able to calculate the inverse Fourier transform of G(S). The density function can be either periodic or non-periodic. Numerous tools including drawing tools can be applied in order to understand the role of amplitudes and phases which are of particular importance in diffraction phenomena. As an illustration, the Patterson function of a periodic structure can be simulated.
The analytic expression of the structure factors, F(hkl), is simple and involves a new magnitude (ƒj ) called atomic scattering factor (defined in a previous chapter) which takes into account the different scattering powers with which the electrons of the j atoms scatter the X-rays:
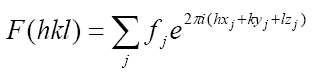
Formula 2. Structure factor for each diffracted beam. This equation is the Fourier transform of the electron density (Formula 1).
The expression takes into account the scattering factors ƒ of all j atoms contained in the crystal unit cell.
From the experimental point of view, it is relatively simple to measure the amplitudes [F(hkl)] of all diffracted waves produced by a crystal. We just need an X-ray source, a single crystal of the material to be studied and an appropriate detector. With these conditions fulfilled we can then measure the intensities, I(hkl), of the diffracted beams in terms of:
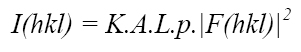
Formula 3. Relationship between the amplitude of the structure factors |F(hkl)| and their intensities I(hkl)
K is a factor that puts the experimental structure factors, (Frel) , measured on a relative scale (which depends on the power of the X-ray source, crystal size, etc.) into an absolute scale, which is to say, the scale of the calculated (theoretical) structure factors (if we could know them from the real structure, Formula 2 above). As the structure is unknown at this stage, this factor can be roughly evaluated using the experimental data by means of the so-called Wilson plot.

Wilson plot
I rel represents the average intensity (in a relative scale) collected in a given interval of θ (the Bragg angle); fj are the atomic scattering factors in that angular range, and λ is the X-ray wavelength.
By plotting the magnitudes shown in the left figure (green dots), a straight line is obtained from which the following information can be derived:
- The value of the y-axis intercept is the Naperian logarithm of C, a magnitude related to the scale factor K (= 1 / √C), described above.
- The slope is equivalent to -2B, where B is the isotropic overall atomic thermal vibration factor.
A is an absorption factor, which can be estimated from the dimensions and composition of the crystal.
L is known as the Lorentz factor, responsible for correcting the different angular velocities with which the reciprocal points cross the surface of Ewald's sphere. For four-circle goniometers this factor can be calculated as 1/sin 2θ, where θ is the Bragg angle of the reflections.
p is the polarization factor, which corrects the polarization effect of the of the incident beam, and is given by the expression (1+cos22θ)/2, where θ also represents the Bragg angle of the reflections (the reciprocal points).
THE PHASE PROBLEM
However, in order to calculate the electron density (ρ(xyz) in Formula 1, above), and therefore to know the atomic positions inside the unit cell, we also need to know the phases of the different diffracted beams (Φ(hkl) in Formula 1 above). But, unfortunately, this valuable information is lost during the diffraction experiment (there is no experimental technique available to measure the phases!) Thus, we must face the so-called phase problem if we want to solve Formula 1.
The phase problem can be very easily understood if we compare the diffraction experiment (as a procedure to see the internal structure of crystals) with a conventional optical microscope...

Illustration on the phase problem. Comparison between an optical microscope and the "impossible" X-ray microscope. There are no optical lenses able to combine diffracted X-rays to produce a zoomed image of the crystal contents (atoms and molecules).
In a conventional optical microscope the visible light illuminates the sample and the scattered beams can be recombined (with intensity and phase) using a system of lenses, leading to an enlarged image of the sample under observation.
In what we might call the impossible X-ray microscope (the process of viewing inside the crystals to locate the atomic positions), the visible light is replaced by X-rays (with wavelengths close to 1 Angstrom) and the sample (the crystal) also scatters this "light" (the X-rays). However, we do not have any system of lenses that could play the role of the optical lenses, to recombine the diffracted waves providing us with a direct "picture" of the internal structure of the crystal. The X-ray diffraction experiment just gives us a picture of the reciprocal lattice of the crystal on a photographic plate or detector. The only thing we can do at this stage is to measure the positions and intensities of the spots collected on the detector. These intensities are proportional to the structure factor amplitudes, [F(hkl)].
But regarding the phases, Φ(hkl), nothing can be concluded for the moment, preventing us from obtaining a direct solution of the electron density function (Formula 1 above).
We therefore need some alternatives in order to retrieve the phase values, lost during the diffraction experiment...
STRUCTURAL RESolution
Once the phase problem is known and understood, let's now see the general steps (see the scheme below) that a crystallographer must face in order to solve the structure of a crystal and therefore locate the positions of atoms, ions or molecules contained in the unit cell...

General diagram illustrating the process of resolution of molecular and crystal structures by X-ray diffraction The process consists of different steps that have been treated previously or are described below:
- Getting a crystal suitable for the experiment, with adequate quality and size. Something related will be seen in another section.
- Obtaining the diffraction pattern with the appropriate wavelength. This has been described in another chapter.
- Evaluating the diffraction pattern to get the lattice parameters (unit cell), symmetry (space group) and diffraction intensities.
- Solving the electron density function, obtaining any information about the phases of the diffracted beams. This is a key point for the structural resolution that will be discussed below.
- Building an initial structural model to explain the values of the electron density function and completing the model locating the remaining atomic positions. This will be seen below.
- Refining the model, adjusting all atomic positions to get the calculated diffraction pattern as similar as possible to the experimental diffraction pattern, and finally validate and show the total structural model obtained. This will be seen in another chapter.
For the study to be successful, some important aspects must be taken into account, such as:
- The compound under study must be pure to be crystallized (if not already, as in the case of natural minerals).
- Crystals can be obtained using different techniques, from the most simple evaporation or slow cooling method up to the more complex: vapor (or solvent) diffusion, sublimation, convection, etc. There is enough literature available.. See, for example, the pages of the LEC, Laboratory of Crystallographic Studies, for additional information on specific crystallization techniques. For proteins, the procedure most extensively used is based on vapor diffusion experiments, usually with the "hanging drop" technique, described elsewhere in these pages. In this sense it is very relevant to note the recent advances introduced in the field of femtosecond X-ray protein nanocrystallography, which will mean a giant step to practically eliminate most difficulties in the crystallization process, and in particular for proteins (see the small paragraph dedicated to the X-ray free electron laser).
- If appropriate crystals are obtained, they are exposed to X-rays and their diffraction intensities measured using the methods and equipment described in a previous chapter. A careful data evaluation will provide us with the dimensions of the unit cell, the symmetry and, directly from the intensities, the amplitudes of the structure factors [F(hkl)] . Of all these subjects at this stage, the most difficult one concerns the determination of the crystal symmetry, a key question for the successful resolution of the structure. To obtain crystal symmetry, a visual study of the crystal would make no sense and therefore it must be deduced from the symmetry of the diffraction pattern, as indicated in a specific section of these pages.
- At this stage, the question about the unknown phases, Φ(hkl), arises, so that they must be somehow evaluated, as we will see below...
- If the evaluated phases are correct, the electron density function ρ(xyz) will show a distribution of maxima (atomic positions) consistent and meaningful from the stereochemical point of view. Once an initial structure is known, some additional steps (construction of the detailed model, mathematical refinement and validation) must be carried out. This will lead us to the so-called final model of the structure.
But let us come back to the most important issue: how do we solve the phase problem?
THE PATTERSON FUNCTION
The very first solution to the phase problem was introduced by Arthur Lindo Patterson (1902-1966).
Basing his work on the inability to directly solve the electron density function (Formula 1 above or below), and after his training (under the U.S. mathematician Norbert Wiener) on Fourier transforms convolution, Patterson introduced a new function P(uvw) (Formula 4, below) in 1934. This formula, which defines a new space (the Patterson space), can be considered as the most important single development in crystal-structure analysis since the discovery of X-rays by Röntgen in 1895 or X-ray diffraction by Laue in 1914.
His elegant formula, known as the Patterson function (Formula 4, below), introduces a simplification of the information contained in the electron density function. The Patterson function removes the term containing the phases, and the amplitudes of the structure factors are replaced by their squares. It is thus a function that can be calculated immediately from the available experimental data (intensities, which are related to the amplitudes of the structure factors). Formally, from the mathematical point of view, the Patterson function is equivalent to the convolution of the electron density (Formula 1, below) with its inverse: ρ(x,y,z) * ρ(-x,-y,-z).
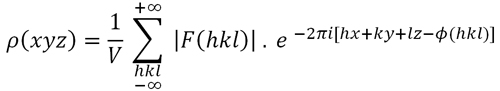
Formula 1. The electron density function calculated at the point of coordinates (x,y,z).
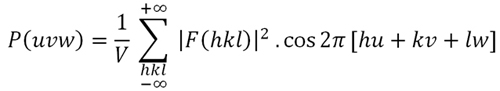
Formula 4. The Patterson function calculated at the point (u, v, w). This is a simplification of Formula 1, since the summation is done on F2(hkl) and all phases are assumed to be zero.
It seems obvious that after omitting the crucial information contained in the phases [Φ(hkl) in Formula 1], the Patterson function will no longer show the direct positions of the atoms in the unit cell, as the electron density function would do.In fact, the Patterson function only provides a map of interatomic vectors (relative atomic positions), the height of its maxima being proportional to the number of electrons of the atoms implied. We will see that this feature means an advantage in detecting the positions of "heavy" atoms (with many electrons) in structures where the remaining atoms have lower atomic numbers. Once the Patterson map is calculated, it has to be correctly interpreted (at least partially) to get the absolute positions (x,y,z) of the heavy atoms within the unit cell. These atomic positions can now be used to obtain the phases Φ(hkl) of the diffracted beams by inverting Formula 1 and therefore this will allow the calculation of the electron density function ρ(xyz), but this will be the object of another section of these pages.
THE DIRECT METHODS
The phase problem for crystals formed by small and medium size molecules was solved satisfactorily by several authors throughout the twentieth century with special mention to Jerome Karle (1918-2013) and Herbert A. Hauptmann (1917-2011), who shared the Nobel Prize in Chemistry in 1985 (without forgetting the role of Isabella Karle, 1921-2017). The methodology introduced by these authors, known as the direct methods, generally exploit constraints or statistical correlations between the phases of different Fourier components.
Left: Herbert A. Hauptman (1917-2011)
Center: Jerome Karle (1918-2013)
Right: Isabella Karle (1921-2017)
The atomicity of molecules, and the fact that the electron density function should be zero or positive at any point of the unit cell, creates certain limitations in the distribution of phases associated with the structure factors. In this context, the direct methods establish systems of equations that use the intensities of diffracted beams to describe these limitations. The resolution of these systems of equations provides direct information on the distribution of phases. However, since the validity of each of these equations is established in terms of probability, it is necessary to have a large number of equations to overdetermine the phase values of the unknowns (phases Φ(hkl)).

The direct methods use equations that relate the phase of a reflection (hkl) with the phases of other neighbor reflections (h',k',l' y h-h',k-k',l-l'), assuming that these relationships are "probably true" (P) ...
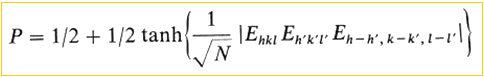
where Ehkl, Eh´k´l´ and Eh-h',k-k',l-l' are the so called "normalized structure factors", that is, structure factors corrected for thermal motion, brought to an absolute scale and assuming that structures are made of point atoms. In other words, structure factor normalization converts measured |F| values into "point atoms at rest" coefficients known as |E| values.
At present, direct methods are the preferred ones for phasing structure factors produced by small or medium sized molecules having up to 100 atoms in the asymmetric unit. However, they are generally not feasible by themselves for larger molecules such as proteins. The interested reader should look into an excellent introduction to direct methods through this link offered by the International Union of Crystallography.
METHODS OF STRUCTURAL RESolution FOR MACROMOLECULES
For crystals composed of large molecules, such as proteins and enzymes, the phase problem can be solved successfully with three main methods, depending of the case:
(i) introducing atoms in the structure with high scattering power. This methodology, known as MIR (Multiple Isomorphous Replacement) is therefore based on the Patterson method.
(ii) introducing atoms that scatter X-rays anomalously, also known as MAD (Multi-wavelength Anomalous Diffraction), and
(iii) by means of the method known as MR (Molecular Replacement), which uses the previously known structure of a similar protein.
MIR (Multiple Isomorphous Replacement)
This technique, based on the Patterson method, was introduced by David Harker, but was successfully applied for the first time by Max F. Perutz and John C. Kendrew who received the Nobel Prize in Chemistry in 1962, for solving the very first structure of a protein, hemoglobin.
Left: David Harker (1906-1991)
Center: Max Ferdinand Perutz (1914-2002)
Right: John Cowdery Kendrew (1917-1997)
The MIR method is applied after introducing "heavy" atoms (large scatterers) in the crystal structure. However, the difficulty of this methodology lies in the fact that the heavy atoms should not affect the crystal formation or unit cell dimensions in comparison to its native form, hence, they should be isomorphic
This method is conducted by soaking the crystal of the sample to be analyzed with a heavy atom solution or by co-crystallization with the heavy atom, in the hope that the heavy atoms go through the channels of the crystal structure and remain linked to amino acid side chains with the ability to coordinate metal atoms (eg SH groups of cysteine). In the case of metalloproteins, one can replace their endogenous metals by heavier ones (for instance Zn by Hg, Ca by Sm, etc.).
Heavy atoms (with a large number of electrons) show a higher scattering power than the normal atoms of a protein (C, H, N, O and S), and therefore they appreciably change the intensities of the diffraction pattern when compared with the native protein. These differences in intensity between the two spectra (heavy and native structures) are used to calculate a map of interatomic vectors between the heavy atom positions (Patterson map), from which it is relatively easy to determine their coordinates within the unit cell.

Scheme of a Patterson function derived from a crystal containing three atoms in the unit cell. To obtain this function graphically from a known crystal structure (left figure) all possible interatomic vectors are plotted (center figure). These vectors are then moved parallel to themselves to the origin of the Patterson unit cell (right figure). The calculated function will show maximum values at the end of these vectors, whose heights are proportional to the product of the atomic numbers of the involved atoms. The positions at these maxima (with coordinates u, v, w) represent the differences between the coordinates of each pair of atoms in the crystal, ie u=x1-x2, v=y1-y2, w=z1-z2.
With the known positions of the heavy atoms, the structure factors are now calculated using Formula 2 (see also the diagram below), that is their amplitudes |Fc(hkl)| and phases Φc(hkl), where the c subscript means "calculated". By using Formula 1, an electron density map, ρ(xyz), is now calculated using the amplitudes of the structure factors observed in the experiment, |Fo(hkl)| (containing the contribution of the whole structure) combined with the calculated phases Φc(hkl). If these phases are good enough, the calculated electron density map will show not only the known heavy atoms, but will also yield additional information on further atomic positions (see diagram below).
In summary, the MIR methodology steps are:
- Prepare one or several heavy atom derivatives that must be isomorphic with the native protein. A first test of isomorphism is done in terms of the unit cell parameters.
- Collect diffraction data from both native and heavy atom derivative(s).
- Apply the Patterson method to get the heavy atom positions.
- Refine these atomic positions and calculate the phases for all diffracted beams.
- Obtain an electron density map with those calculated phases.
MAD (Multi-wavelength Anomalous Diffraction)
The changes in the intensity of the diffraction data produced by introducing heavy atoms in the protein crystals can be regarded as a chemical modification of the diffraction experiment. Similarly, we can cause changes in the intensity of diffraction by modifying the physical properties of atoms. Thus, if the incident X-ray radiation has a frequency close to the natural vibration frequency of the electrons in a given atom, the atom behaves as an "anomalous scatterer". This produces some changes in the atomic scattering factor, ƒj (see Formula 2), so that its expression is modified by two terms, ƒ' and ƒ'' which account for its real and imaginary components, respectively. For atoms which behave anomalously, its scattering factor is given by the expression shown below (Formula 5).
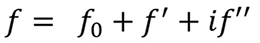
Formula 5. In the presence of anomalous scattering, the atomic scattering factor, ƒ0 , has to be modified adding two new terms, a real and an imaginary part.
The advanced reader should also read the section about the phenomenon of anomalous dispersion.
The ƒ' and ƒ'' corrections vs. X-ray energy (see below for the case of Cu Kα) can be calculated taking into account some theoretical considerations...

Real and imaginary components of the Selenium scattering factor vs. the energy of the incident X-rays. The vertical line indicates the wavelength for CuKα.
For X-ray energy values where resonance exists, ƒ' increases dramatically, while the value of ƒ'' decreases. This has practical importance considering that many heavy atoms used in crystallography show absorption peaks at energies (wavelengths) which can be easily obtained with synchrotron radiation. Diffraction data collected in these conditions will show a normal component, mainly due to the light atoms (nitrogen, carbon and hydrogen), and an anomalous part produced by the heavy atoms, which will produce a global change in the phase of each reflection. All this leads to an intensity change between those reflections known as Friedel pairs (pairs of reflections which under normal conditions should have the same amplitudes and identical phases, but with opposite signs). The detectable change in intensity between these reflection pairs (Friedel pairs) is what we call anomalous diffraction.
The MAD method, developed by Hendrickson and Kahn, involves diffraction data measurement of the protein crystal (containing a strong anomalous scatterer) using X-ray radiations with different energies (wavelengths): one that maximizes ƒ'', another which minimizes ƒ' and a third measurement at an energy value distinct from these two. Combining these diffractions data sets, and specifically analyzing the differences between them, it is possible to calculate the distribution of amplitudes and phases generated by the anomalous scatterers. The subsequent use of the phases generated by these anomalous scatterers, as a first approximation, can be used to calculate an electron density map for the whole protein.
In general, there is no current need to introduce individual atoms as anomalous scatterers in protein crystals. It is relatively easy to obtain recombinant proteins in which methionine residues are replaced by selenium-methionine. Selenium (and even sulfur) atoms of methionine (or cysteine), behave as suitable anomalous scatterers for carrying out a MAD experiment.
The MAD method presents some advantages vs. the MIR technique:
- As the MAD technique uses data collected from a single crystal, the problems derived from lack of isomorphism, common in the MIR method, do not apply.
- While in the absence of anomalous dispersion, the atomic scattering factor (ƒ0) decreases dramatically with the angle of dispersion, its anomalous component (ƒ' + iƒ'' ) is independent of that angle, so that this relative signal increases at a higher resolution of the spectrum, which is to say, at high Bragg angles. Thus, the estimates of phases by MAD are generally better at high resolution. On the contrary, with the MIR method, the lack of isomorphism is larger at high resolution angles and therefore the high resolution intensities (> 3.5 Angstrom) are not suitable for phasing.
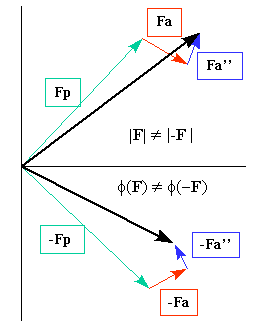
Argand diagram showing the scattering contribution from an anomalous scatterer in a matrix of normal scatterers. This effect implies that Friedel's law fails. Image taken from "Crystallography 101".
- Fp represents the contribution from the normal scatterers to the structure factor (of indices hkl).
- Fa and Fa''represent the real (ƒ0 + ƒ' ) and imaginary (ƒ'' ) parts, respectively, of the scattering factor from the anomalous scatterers.
- -Fp, -Fa and -Fa" represent the same as Fp, Fa and Fa'', but for the reflection with indices -h, -k, -l.
The anomalous behavior of the atomic scattering factor only produces small differences between the intensities (and therefore among the amplitudes of the structure factors) of the reflections that are related by a centre of symmetry or a mirror plane (such as for instance, I(h,k,l) vs. I(-h,-k,-l), or I(h,k,l) vs. I(h,-k,l). Therefore, to estimate these small differences between the experimental intensities, additional precautions must be taken into account. Thus, it is recommended that reflections expected to show these differences are collected on the same diffraction image, or alternatively, after each collected image, rotate the crystal 180 degrees and collect a new image. Moreover, since changes in ƒ' and ƒ'' occur by minimum X-ray energy variations, it is necessary to have good control of the energy values (wavelengths). Therefore, it is essential to use a synchrotron radiation facility, where wavelengths can be tuned easily.
The advanced reader should also have a look into the web pages on anomalous scattering, prepared by Bernhard Rupp, as well as the practical summary prepared by Georg M. Sheldrick.
MR (Molecular Replacement)
If we know the structural model of a protein with a homologous amino acid sequence, the phase problem can be solved by using the methodology known as molecular replacement (MR). The known structure of the homologous protein is regarded as the protein to be determined and serves as a first model to be subsequently refined. This procedure is obviously based on the observation that proteins with similar peptide sequences show a very similar folding. The problem in this case is transferring the molecular structure of the known protein from its own crystal structure to a new crystal packing of the protein with an unknown structure. The positioning of the known molecule into the unit cell of the unknown protein requires determining its correct orientation and position within the unit cell. Both operations, rotation and translation, are calculated using the so-called rotation and translation functions (see below).

Scheme of the molecular replacement (MR) method.
The molecule with known structure (A) is rotated through the [R] operation and shifted through T to bring it over the position of the unknown molecule (A’).
The rotation function. If we consider the case of two identical molecules, oriented in a different way, then the Patterson function will contain three sets of vectors. The first one will contain the Patterson vectors of one of the molecules, ie all interatomic vectors within molecule one (also called eigenvectors). The second set will contain the same vectors but for the second molecule, identical to the first one, but rotated due to their different orientation. The third set of vectors will be the interatomic cross vectors between the two molecules. While the eigenvectors are confined to the volume occupied by the molecule, the cross vectors will extend beyond this limit. If both molecules (known and unknown) are very similar in structure, the rotation function R(α,β,γ) would try to bring the Patterson vectors of one of the molecules to be coincident with those of the other, until they are in good agreement. This methodology was first described by Rossman and Blow.
R(α,β,γ) = ∫u P1(u) x P2(ur) du
Formula 6. Rotation function
P1 is the Patterson function and P2 is the rotated Patterson function, where u is the volume of the Patterson map, where interatomic vectors are calculated.
The quality of the solutions of these functions is expressed by the correlation coefficient between both Patterson functions: the experimental one and the calculated one (with the known protein). A high correlation coefficient between these functions is equivalent to a good agreement between the experimental diffraction pattern and the diffraction pattern calculated with the known protein structure. Once the known protein structure is properly oriented and translated (within the unit cell of the unknown protein), an electron density map is calculated using these atomic positions and the experimental structure factors. It is worth consulting the article published on this methodology by Eleanor Dodson.
Probably it is valuable for the advanced reader to consult a nice article that, despite having been published in 2010, has not lost its validity in relation to the description of the different methodologies for the determination of the relative phases of the diffraction beams.
COMPLETING THE STRUCTURE
All these methods (Patterson, direct methods, MIR, MAD, MR) provide (directly or indirectly) knowledge about approximate phases which must be upgraded. As indicated above, the calculated initial phases, Φc(hkl), together with the observed experimental amplitudes, |Fo(hkl)|, allow us to calculate an electron density map, also approximate, over which we can build the structural model. The overall process is summarized in the cyclic diagram shown below.
The initial phases, Φc(hkl), are combined with the amplitudes of the experimental (observed) structure factors, |Fo(hkl)|, and an electron density map is calculated (shown at the bottom of the scheme). Alternatively, if the initial known data are the coordinates (xyz) of some atoms, they will provide the initial phases (shown at the top of the scheme), and so on in a cyclic way until the process does not produce any new information.

Scheme showing a cyclic process to calculate electron density maps ρ(xyz) which produce further structural information.
From several known atomic positions we can always calculate the structure factors: their amplitudes, |Fc(hkl)|, and their phases, Φc(hkl),as shown at the top of the scheme. Obviously, the calculated amplitudes can be rejected, because they are calculated from a partial structure and the experimental ones represent the whole and real structure. Therefore, the electron density map (shown at the bottom of the scheme) is calculated with the experimental (or observed) amplitudes, |Fo(hkl)|, and the calculated phases, Φc(hkl). This function is now evaluated in terms of possible new atomic positions that are added to the previously known ones, and the cycle repeated. Historically this process was known as "successive Fourier syntheses", because the electron density is calculated in terms of a Fourier sum.
In any case, from atomic positions or directly from phases, if the information is correct, the function of electron density will be interpretable and will contain additional information (new atomic coordinates) that can be injected into the cyclic procedure shown above until structure completion, which is to say until the calculated function ρ(xyz) shows no changes from the last calculation.
The lighter atoms of the structure (those with lower atomic number, ie, usually hydrogen atoms) are the most difficult ones to find on an electron density map. Their scattering power is almost obscured by the scattering of the remaining atoms . For this reason, the location of H atoms is normally done via a somewhat modified electron density function (the difference electron density), whose coefficients are the differences between the observed and calculated structure factors of the model known so far:
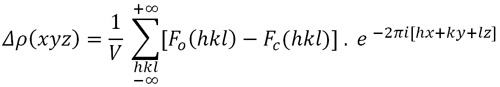
Formula 7. Function of "difference" electron density
In practice, if the structural model obtained is good enough, if the experiment provided precise structure factors, and there are no specific errors such as X-ray absorption, the difference map Δρ will contain enough signal (maxima) where H atoms can be located. Additionally, to get an enhanced signal from the light atoms scattering, this function is usually calculated with the structure factors appearing at lower diffraction angles only, usually with those appearing at sin θ / λ < 0.4, that is, using the region where the scattering factors for hydrogens are still "visible".









