1.5: Scattering and diffraction
- Page ID
- 352424
In the context of this chapter, you will also be invited to visit these sections...
- Group velocity
- Kinematic model
- Optical diffraction diagrams
- The Laue equations
- The Bragg's Law
- The Bragg's Law ("applet")
- The structure factor
- The Fourier transform



Center: Refraction of light after passing through a glass prism. Depending on the wavelength (color) of the incident beam (coming from the left), the angle of refraction varies, ie: it is scattered
Right: Polarization of light passing through a polarizer. Depending on the rotation of the polarizer, one of components of the incident beam (coming from the right) is filtered
X-ray diffraction is the physical phenomenon that expresses the fundamental interaction between X-rays and crystals (ordered matter). However, to describe the phenomenon, it is advisable to first introduce some physical models that (as all models) do not fully explain reality (as they are an idealization of it), but can be used to help understand the phenomenon.
On waves
A wave is an undulatory phenomenon (a disturbance) that propagates through space and time, and is regularly repeated.

Waves are usually represented graphically by a sinusoidal function (as shown at right), in which we can determine some general parameters that define it.


Transverse wave propagation of vibrating longitudinal and circular movements Animations originally taken from physics-animations.com
Undulatory phenomena (waves) propagate at a certain speed (v) and can be modeled to meet the so-called wave equation, scalar or vectorial, depending on the nature of the disturbance. The solutions to this equation are usually combinations of trigonometric terms, each of them characterized by: 1) an amplitude (A), which measures the maximum (or minimum) of the disturbance with respect to an equilibrium value, and 2) a phase \(\phi\):
\(\phi\) = 2\(\pi\) (K.r - ν.t + \(\alpha\))
The intensity of an undulatory disturbance, at any point of the wave, is proportional to the square of the disturbance value at that point, and if it is expressed in terms of complex exponentials, this is equivalent to the product of the disturbance by its complex conjugate. The intensity is a measure of the energy flow per unit of time and per unit of area of the wavefront (spherical or flat, depending on the type of wave).
A wave is a regular phenomenon, ie it repeats exactly in time (with a period T) and space (with a period λ, the wavelength), so that λ = ν.T, or λ.ν= v.
In the expression of the phase (\(\phi\)), K is the so-called wave vector which gives the sense of progress of the wave (the ray), and is considered with an amplitude 1/λ. Thus, K is the number of repetitions per unit of length.
ν is the frequency (the inverse of the period), that is, the number of repetitions (or cycles) per unit of time. We give the name pulse to the magnitude given by: 2\(\pi\).ν, which measures the number of repetitions per radian (180/π degrees) of the cycle.
In the full electromagnetic spectrum (ie in the distribution of electromagnetic wavelengths) the hard X-rays (the high energy ones) are located around a wavelength of 1 Angstrom in vacuum (for Cu the average wavelength is 1.5418 Angstrom and for Mo it's 0.7107 Angstrom), while visible light has a wavelength in the range of 4000 to 7000 Angstrom.
t and r are, respectively, the time and the position vector with which we measure the disturbance, and \(\alpha\) is the original phase difference relative to the other components of the wave.
We speak of waves being in phase if the difference between the phases of the components is an integer multiple of 2\(\pi\), and we say that the waves are in opposition of phase if that difference is an odd multiple of \(\pi\). For an easy mathematical treatment to keep track of the relations between phases of the wave components, these terms are usually expressed in an exponential notation, where the exponential imaginary unit i means a phase difference of +\(\pi\)/2.
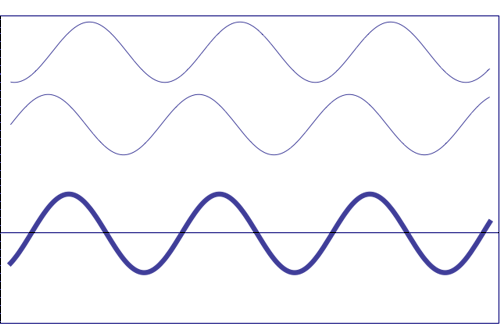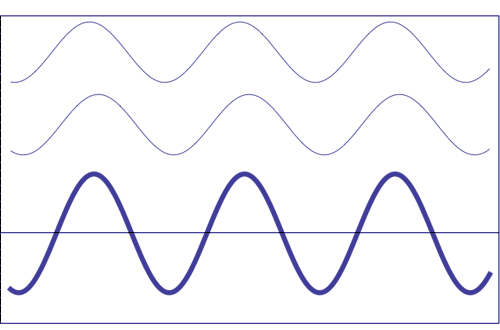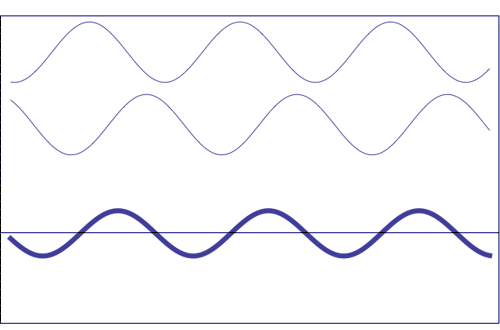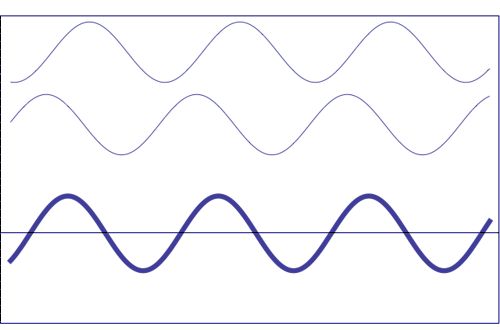
Possible states of interference of two waves shown at the top, having identical amplitude and frequency. The wave drawn at the bottom (bold line) shows the result of the interference, which has maximum amplitude when interfering waves overlap, i.e. they are in phase. Complete destructive interference is obtained (resulting wave vanishes) when the maxima of one of the component waves coincide with the minima of the other, i.e., when the two waves are in phase opposition. Animation taken from The Pennsylvania State University

Undulatory disturbance corresponding to the combination of two elementary waves (blue and green) of similar wavelengths (λ, λ), with the same amplitude (A, A) and relative difference of phase \(\alpha\). The disturbance is moving from left to right with a velocity v. The sum of these two elementary waves produces a wave (sum of the individual ones) depicted in red (λ).
Interference usually refers to the interaction of waves which are correlated or coherent with each other, either because they come from the same source or because they have the same, or nearly the same, frequency.
The solutions to the wave equation, whose amplitude is not inversely dependent on the distance of origin, are called plane waves, since at a given time all points belonging to the plane K.r = constant have the same phase, the plane is perpendicular to the propagation vector K, and propagates with speed v.
v is therefore the phase velocity. For a wave resulting from the sum of several components, the pulse travels with the so-called group velocity and interested readers can consult the simulation offered through this link.
In the solutions to the equation in which the amplitude depends inversely on the distance, the planes become spheres and thus spherical waves are obtained. However if the distance of observation is very large, they can be considered similar to plane waves at that observation point.
Taking into account what it is shown in the figure above, the principle of superposition states that due to a number of coherent sources (which don't vary phase relationships between them), the wave measured at a given time and point, is the sum of the individual waves at that time and point, taking into account the individual phases (the process of interference), as shown above.
If there is no coherence between waves, phase relationships vary over time, and to obtain the total intensity of the resultant wave, we just have to add intensities (see figure below):

The total disturbance of two non-coherent sources is just the sum of the individual intensities
To model the composition of simple trigonometric waves (of type sine or cosine, or in their imaginary exponential form) the Fresnel representation is normally used. In this representation it is assumed that each wave oscillates around the X axis, as the projection of the circular motion of a vector of length equal to its amplitude and with an angular speed equal to the wave pulse ω. In this way, the resultant wave can be obtained by adding the individual vectors and projecting the resultant vector over the same X axis.

Fresnel (or Argand) representation in which is shown the composition of several individual waves (fj).
|F| is the amplitude of the resultant wave and Φ its phase.
Interaction of X-rays with matter
X-ray waves interact with matter through the electrons contained in atoms, which are moving at speeds much slower than light. When the electromagnetic radiation (the X-rays) reaches an electron (a charged particle) it becomes a secondary source of electromagnetic radiation that scatters the incident radiation.
According to the wavelength and phase relationships of the scattered radiation, we can refer to elastic processes (or inelastic processes: Compton scattering), depending if the wavelength does not change (or changes), and to coherence (or incoherence) if the phase relations are maintained (or not maintained) over time and space.
The exchanges of energy and momentum that are produced during these processes can even lead to the expulsion of an electron out of the atom, followed by the occupation of its energy level by electrons located in higher energy levels.
All these types of interactions lead to different processes in the materials such as: refraction, absorption, fluorescence, Rayleigh scattering, Compton scattering, polarization, diffraction, reflection, ...
The refractive index of all materials in relation to X-rays is close to 1, so that the phenomenon of refraction of X-rays is negligible. This explains why we are not able to produce lenses for X-rays and why the process of image formation, as in the case of visible light, cannot be carried out with X-rays. It does not explain why reflective optics (catoptric system) cannot be used. Only dioptric system is excluded.
Absorption means an attenuation of the transmitted beam, losing its energy through all types of interactions, mainly thermal, fluorescence, inelastic scattering, formation of free radicals and other chemical modifications that could lead to degradation of the material. This intensity decrease follows an exponential model dependent on the distance crossed and on a coefficient of the material (the linear absorption coefficient) which depends on the density and composition of the material.
The process of fluorescence, in which an electron is pulled out of an atom's energy level, provides information on the chemical composition of the material. Due to the expulsion of electrons from the different energy levels, sharp discontinuities in the absorption of radiation are produced. These discontinuities allow local analysis around an atom (EXAFS).
In the Compton effect, the interaction is inelastic and the radiation loses energy. This phenomenon is always present in the interaction of X-rays with matter, but due to its low intensity, its incoherence and its propagation in all directions, its contribution is only found in the background radiation produced through the interaction.
By scattering we will refer here to the changes of direction suffered by the incident radiation, and NOT to dispersion (the phenomenon that causes the separation of a wave into components of varying frequency).
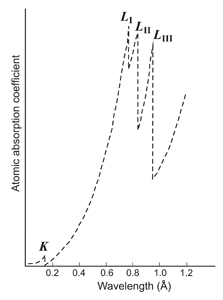
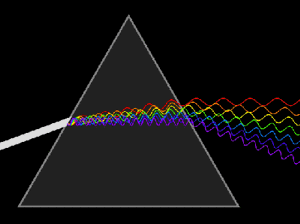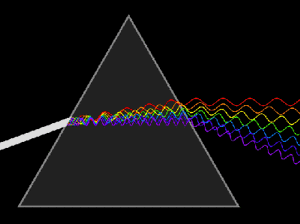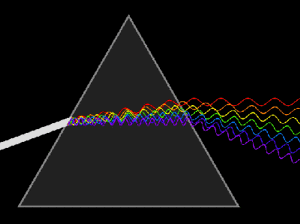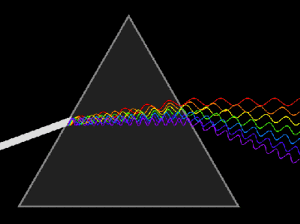
Left: Variation in the absorption of a material according to the wavelength of the incident radiation
Right: Dispersion of visible light into its nearly monochromatic wavelengths
Elastic scattering by an electron

Interaction of a X-ray front with an isolated electron, which becomes a new X-ray source, producing the X-rays waves in a spherical mode

The spherical waves produced by two electrons interact with each other, producing positive and negative interferences
Animations originally taken from physics-animations.comWhen a non-polarized X-ray beam (that is, when its electromagnetic field is vibrating at random in all directions perpendicular to the propagation), interacts with an electron, the interaction takes place primarily through its electric field. Thus, in a first approximation, we can neglect both the magnetic and nuclear interactions. According to the electromagnetic theory of Maxwell, the electron scatters electric waves which propagate perpendicular to the electric field, in such a way that the scattered energy (which crosses the unit of area perpendicular to the direction of propagation and per unit of time) is:
Ie(Ks) = I0 [e4 / R02 m2 c4] [( 1 + cos2 2θ) / 2]

Thomson scattering model
Ks is the scattering vector, R0 is the distance to the observation point, 2θ is the angle between the incident direction and the direction where the scattering is observed; e and m are the charge and mass of the electron, respectively, and c is the speed of propagation of radiation in the vacuum.
The equation above describes the Thomson's model established in 1906 [Joseph John Thomson (1856-1940)] for the spherical wave elastically scattered by a free electron, which is similar to the Rayleigh scattering with visible light. The scattered wave is elastic, coherent and spherical. The mass factor (m) in the denominator justifies neglecting the nuclear scattering.
The binding forces between atom and electron are not considered in the model. It is assumed that the natural frequencies of vibration of the electron are much smaller than those of the incident radiation. In this "normal" scattering model (in contrast to the anomalous case in which those frequencies are comparable) the scattered wave is in opposition of phase with the incident radiation.
The second factor (in brackets equation above) which depends on the θ angle, is known as the polarization factor, because the scattered radiation becomes partially polarized, which creates a certain anisotropy in the vibrational directions of the electron, as well as a reduction in the scattered intensity (depending of the direction). The scattered intensity shows symmetry around the incident direction. As the scattered wave is spherical, the inverse proportionality to the squared distance makes the energy per unit of solid angle a constant.
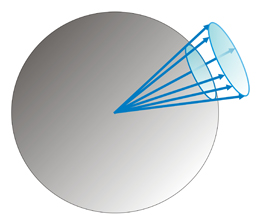
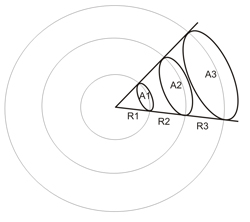
A solid angle is the angle in three-dimensional space that an object subtends at a point. It is a measure of how big that object appears to an observer looking from that point. Metrically it is the constant ratio between the intersecting areas of concentric spheres with a cone, and the corresponding squared radii of the spheres:
A1/R12 = A2/R22 = A3/R32 = ... = solid angle in steradians
The factor of the geometric "difference of phase"
With regard to the phenomenon of diffraction and interference, it is important to consider the phase relationship between two waves due to their different geometric paths. This affects the difference of phase \(\alpha\) of the resultant wave:
\(\phi\) = 2\(\pi\)(K0.r - ν.t + \(\alpha\))
\(\alpha\) = 2\(\pi\) (Ks - K0) rij + \(\alpha\) '
where K0 is the wave vector of the incident wave, Ks is the wave vector in the direction of propagation and rij is the vector between the two propagation centers which produces the phase difference.
If we have several disturbance centers whose phase differences are measured from a common origin, and we consider the position vectors rj of their phase differences, the phase difference of one of the centers can be written (using unit vectors in the directions of propagation with λK = s) as:
\(\alpha\)j = 2\(\pi\) [(s - s0) / λ] rj + \(\alpha\) '
This means that all rj points in which the product (s - s0) rj has a constant value (cte) , will have the same phase, given by:
\(\alpha\) = (cte. 2\(\pi\) / λ) + \(\alpha\) '
Scattering by an atom
An atom that can be considered as a set of Z electrons (its atomic number) can be expected to scatter Z times that which an electron does. But the distances between the electrons of an atom are of the order of the X-rays wavelength, and therefore we can also expect some type of partial destructive interferences among the scattered waves. In fact, an atom scatters Z times (what an electron does) only in the direction of the incident beam, decreasing with the increasing of the θ angle (the angle between the incident radiation and the direction where we measure the scattering). And the more diffuse the electronic distribution of electrons around the nucleus, the greater the reduction.

Phase relationships among the electrons in an atom
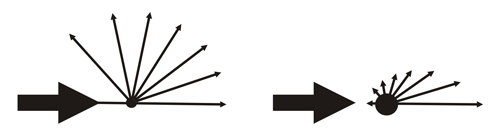
Diagram showing the variation of the amplitudes scattered by an electron, without considering the polarization (left figure), and an atom (right figure). The amplitude (intensity) scattered by an atom decreases with increasing scattering angle.

The intensity of the X-rays scattered by the electrons of an atom decreases with increasing scattering angle
Scheme taken from School of Crystallography (Birkbeck College, Univ. of London)
The atomic scattering factor is the ratio between the amplitude scattered by an atom and a single electron. As the speed of electrons in the atom is much greater than the variation of the electric vector of the wave, the incident radiation only "sees" an average electronic cloud, which is characterized by an electron density of charge ρ(r). If this distribution is considered spherically symmetric, it will just depend on the distance to the nucleus, so that, with:
H = 2 sin θ / λ (which is the length of the scattering vector H = Ks- K0 = (s - s0) / λ):
f(H) = 4π∫(0 → ∞) r2 ρ(r) (sin H r / H r) dr
Thus, the atomic scattering factor will represent a number of electrons (the effective number of electrons of a particular atom type) that scatter in phase in that direction, so that θ = 0 and f(0) = Z. The hypothesis of isotropy, ie that this atomic factor does not depend on the direction of H, appears to be unsuitable for transition momentum in which d or f orbitals are involved, nor for the valence electrons.
By quantum-mechanics calculations we can obtain the values for the atomic scattering factors, and we can derive analytical estimates of the type:
f(H) = Σ(1 → 4) ai exp [ -bi H2 ] + c

Left: Atomic scattering factors calculated for several ions with the same number of electrons as Ne. One can observe that the O-- has a more diffuse electronic cloud than Si 4+ and thus it shows a faster decay
Right: Atomic scattering factors calculated for atoms and ions with different numbers of electrons. Note that the single electron of the hydrogen atom (H) scatters very little as compared with other elements, especially with increasing Θ. Hydrogen will therefore be "difficult to see" among other dispersion effects
When the frequency of the incident radiation is close to the natural vibration of the electron linked to the atom, we have to make some corrections (Δ) due to the phase differences that occur between the individual waves scattered by electrons, whose vibration (due to the incident wave) is affected by that linking. Thus:
f(H) = f0 + Δ' f + i Δ'' f
also written as:
f(H) = f0 + f ' + i f ''
where f0 is the atomic scattering factor without ligation, as previously defined, and i is the imaginary unit that represents the phase differences between individual scattered waves. This situation occurs for atoms with large atomic numbers (heavy atoms), or with atomic numbers close (but smaller) to the metal atoms in the X-ray anode. These corrections, that will be discussed in another chapter, weakly depend on the θ angle, so that this anomalous effect is better seen at larger values of this angle, although this is where the scattered beams have lower intensity due to thermal effects (see below).
[These corrections allow us to distinguish the chirality (Bijvoet, 1951) of the crystals and provide us a method for solving the structure of molecules (SAD, MAD)].
Due to the movement of the atomic thermal vibrations within the material, the effective volume of the atom appears larger, leading to an exponential decrease of the scattering power, characterized by a coefficient B (initially isotropic) in the Debye-Waller (1913, 1923) exponential factor:
f(H) exp [ -Biso sin2θ / λ2 ]
B is 8π2<u2>, <u2> being the quadratic average amplitude of thermal vibration in the H direction. In the isotropic model of vibration, B is considered to be identical in all directions (with normal values between 3 and 6 Angstroms2 in crystals of organic compounds). In the anisotropic model, B is considered to follow an ellipsoidal vibration model. Unfortunately, these thermal parameters may reflect not only thermal vibration, as they are affected by other factors such as atomic static disorder, absorption, wrong scattering factors, etc.

Decrease of the atomic scattering factor due to the thermal vibration
If the browser allows it, interested readers can also use this applet made by Steffen Weber which shows the decrease of the atomic scattering factor of an atom when the temperature increases its thermal vibration state. Just write in the left column of the applet the atomic number of an atom (eg 80 for mercury), and the same number in the box shown below. Then activate the box marked with the word "Execute" and note the decrease of the scattering factor as a function of the selected temperature. Now increase the temperature (eg 2), and re-activate the "Execute" box.
Scattering by a set of atoms
X-rays scattered by a set atoms produce X-ray radiation in all directions, leading to interferences due to the coherent phase differences between the interatomic vectors that describe the relative position of atoms. In a molecule or in an aggregate of atoms, this effect is known as the effect of internal interference, while we refer to an external interference as the effect that occurs between molecules or aggregates. The scattering diagrams below show the relative intensity of each of these effects:
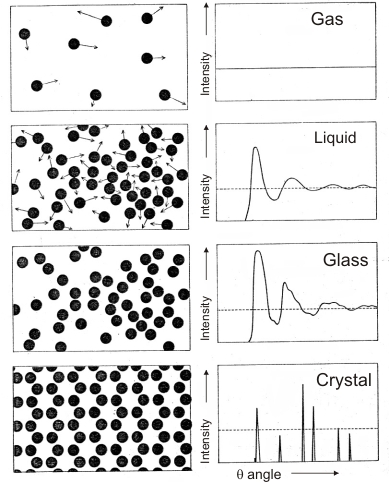
Scattering diagrams of a monoatomic material in different states. In the intensity axis we have neglected the background contribution. The figures mainly represent the effect of the external interference, while the internal interference (in this case due to a single atom only) is simply reflected by the relative intensity of the maxima. Note how the thermal movement in the liquid softens and reduces the scattering profile, and how the maxima produced by the glass also decrease. In the crystal, where the phase relations are fixed and repetitive, the scattering profile becomes sharp with well defined peaks, whereas in the other diagrams the peaks are broad and somewhat continuous. In the crystal case the scattering effect is known as diffraction. Note how the scattering phenomenon reflects the internal order of the sample -- the positional correlations between atoms.
In the case of monoatomic gases, the effects of interference between atoms m and n lead (in terms of the intensity scattered by an electron) to:
I(H) = Ie(H) ΣmΣn fm(H) fn(H) exp [2\(\pi\)i (s - s0) rm,n / λ]
which, when averaged over the duration of the experiment and in all k directions of space, gives rise to the Debye formula:
<I(H)> = Ie(H) ΣmΣn fm(H) fn(H) [ sin 2π|H| |rm,n| / 2π|H| |rm,n| ]
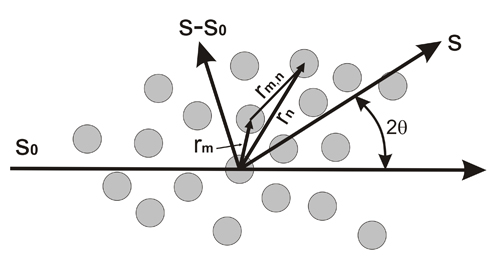
Geometry of the scattering produced by a set of identical atoms
In the case of monoatomic liquids some effects appear at short distances, due to correlations between atomic positions. If the density of atoms per unit of volume (at a distance r from any atom with spherical symmetry) is, on average, ρ(r), then the expression 4\(\pi\) r2ρ(r) is known as the radial distribution, and the Debye formula becomes:
<I(H)> = Ie(H) N f2(H) [ 1 + ∫(0 → ∞) 4\(\pi\)r2ρ(r) sin (2\(\pi\)|H| |r|) / 2\(\pi\)|H| |r| dr ]
All these relationships allow the analysis of the X-ray scattering in amorphous, glassy, liquid and gaseous samples.
No matter the possible complexity with which the phenomenon of X-ray scattering is presented. The nonspecialist reader should only remember some simple ideas that are outlined below (drawings taken from the lecture by Stephen Curry)...
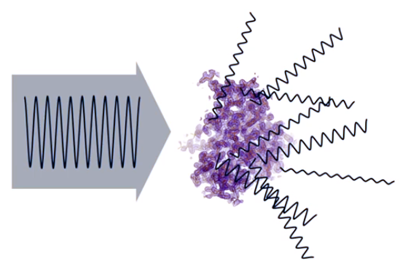
- X-rays are scattered by electrons contained in atoms. This dispersion effect (which is produced in the form of waves, scattered in all directions of space) contains different intensities (amplitudes), depending on the number of electrons (electron density) contributing to the scattered waves...
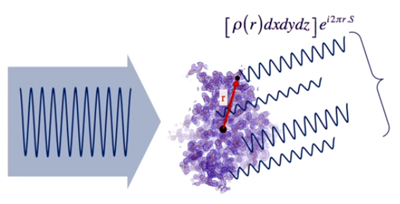
- Taking an origin in the atomic set and considering a given direction of dispersion, each of the waves scattered in that direction can be represented by a mathematical function (shown in the figure), whose amplitude depends on the electron density ρ(r) existing at the point where the wave arises. S is a magnitude which depends on the angle at which the scattering occurs.

- The total scattered wave in each direction is the sum of all the individual waves which scatter in the same direction, f (S). Its intensity (amplitude) will be governed by the phase relationship between the contributing waves, which depends on r (the distance between the points where they originate). This will happen for all space directions...
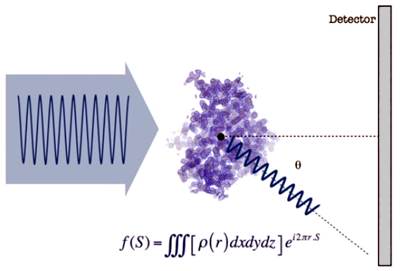
- If we place a detector (such as a photographic plate) to observe the scattered waves, f(S), we obtain a distribution of intensities as shown in the image below...

- This "map" of scattered waves (shape and intensities) contains information on the distribution of atoms that are producing the scattering. Mathematically this map is represented by the function f(S), which is the Fourier transform of the atomic distribution, that is, of the electron density function…

- We will see later that when the set of atoms are arranged in an orderly fashion, ie, in the form of a crystal, they behave as a very effective dispersion amplifier...

- In these circumstances, scattering effects concentrate in certain areas of the detector, very well defined and regularly distributed, known as diffraction... The diffraction allows us to obtain an information about the electronic distribution much richer than the one produced by the scattering of a set of disordered atoms...
Scattering by a monoatomic lattice: Diffraction
When the set of atoms is structured as a regular three-dimensional lattice (so that the atoms are nodes of the lattice), the precise geometric relationships between the atoms give rise to particular phase differences. In these cases, cooperative effects occur and the sample acts as a three-dimensional diffraction grid. Under these conditions, the effects of external interference produce a scattering structured in terms of peaks with maximum intensity which can be described in terms of another lattice (reciprocal of the atomic lattice) which shows typical patterns, such as those you can see when you look at a streetlight through an umbrella or a curtain.
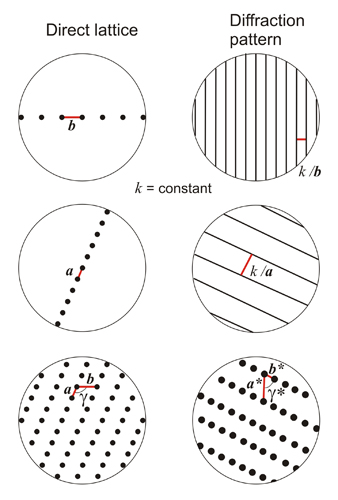
Schematic diagram of diffraction patterns from several two-dimensional point distributions. The parameters of repetition in the diffraction patterns (reciprocal space) carry the * superscript and k means a constant scale factor which depends on the experiment. All points of the diffraction pattern have the same intensity, because it is assumed that the used wavelength is much larger than the points of the direct lattice (see above in the paragraph about scattering by an atom).
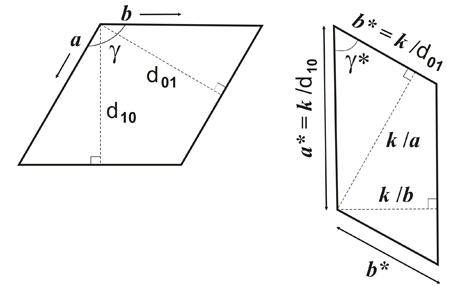
Relationship between two 2-dimensional lattices, direct lattice (on the left) and reciprocal lattice (on the right). The repetition parameters in reciprocal space carry the * superscript and k is a scale factor that depends on the experiment.
d10 and d01 are the corresponding direct lattice spacings. Note that the figures show a direct unit cell and a reciprocal unit cell only, corresponding to the diffraction patterns shown on the left side of the page. See also direct and reciprocal lattices.
Structured in a lattice, any atom can be defined by a vector, referred to a common origin:
R j,m1,m2,m3 = m1 a + m2 b + m3 c
where Rj represents the position of the j node in the lattice; m1, m2, m3, are integers and a, b and c are the vectors defining the lattice. According to this, the intensity scattered by a material would be:
I(H) = Ie(H) Σm1Σm'1Σm2Σm'2Σm3Σm'3 fj(H) fj'(H) exp [2\(\pi\)i (s - s0) rm,m' / λ]
where:
rm,m' = Rm1,m2,m3 - Rm'1,m'2,m'3 = (m1-m'1) a + (m2 - m'2) b + (m3 - m'3) c
And calculating this sum we have:
I(H) = Ie(H) [ [ sin2 π(s - s0) M1 a / λ ] / [sin2 π(s - s0) a / λ ] ] .
[ [ sin2 π(s - s0) M2 b / λ ] / [sin2 π(s - s0) b / λ ] ] .
[ [ sin2 π(s - s0) M3 c / λ ] / [sin2 π(s - s0) c / λ ] ]
= Ie(H) IL(H)
In this expression, M1, M2, M3 represent the number of unit cells contained in the crystal along the a, b and c directions, respectively, so that in the total sample the number of unit cells would be M = M1.M2.M3 (around 1015 in crystals of an average thickness of 0.5 mm).
IL(H) is the factor of external interference due to the monoatomic lattice. It consists of several products of type (sin2 Cx) / sin2 x, where C is a very large number. This function is almost zero for all x values, except in those points where x is an integer multiple of \(\pi\), where it takes its maximum value of C2. The total value would be a maximum value only when all three products are other than zero, where it will take the value of M2. That is, the diffraction diagram of the direct lattice is another lattice that takes non-zero values in its nodes and that, due to the Ie(H) factor, varies from one place to another...
Due to the finite size of the samples, the small chromatic differences of the incident radiation, the mosaic of the sample, etc., the maxima show some type of spreading around them. Therefore, in order to set the experimental conditions for measurement, one needs a small sample oscillation around the maximum position (rocking) to integrate all these effects and to collect the total scattered energy.

Graphical representation of one of the products of the IL(H) function between two consecutive maxima.
Note the transformation from scattering to diffraction, that is, from broad to very sharp peaks, as the number of cells M1 increases.
The maxima are proportional to M12 and the first minimum appears closer to the maximum with increasing M1.
Diffraction by a crystal
When the material is not structured in terms of a monoatomic lattice, but is formed by a group of atoms of the same or of different types, the position of every atom with respect to a common origin is given by:
R j,m1,m2,m3 = m1 a + m2 b + m3 c + rj= Tm1,m2,m3 + rj
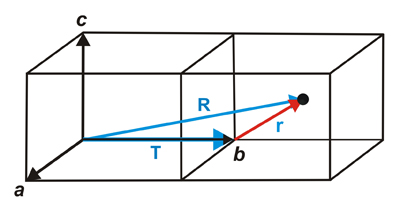
Reduction inside a unit cell of the absolute position of an atom through lattice translations
that is, that to go from the origin to the atom, at position R, we first go, through the T translation, to the unit cell origin, and from there with the vector r we reach the atom.
As the atom is always included within a unit cell, its coordinates referred to the cell are smaller than the axes, and often are expressed as fractions of them:
r = X a + Y b + Z c = X/a a + Y/b b + Z/c c = x a + y b + z c
where x, y, z, as fractions of axes, are now between -1 and +1.
Then, under the conditions initially raised, ie with a monochromatic and depolarised X-ray beam (as a plane wave, formed by parallel rays of a common front wave), perpendicular to the propagation unit vector s0 that completely covers the sample, the kinematic model of interaction indicates that the sample produces diffracted beams in the direction s with an intensity given by:
I(H) = Ie(H) IF(H) IL(H)
where Ie is the intensity scattered by an electron, IL is the external interference effect due to the three-dimensional lattice structure, and IF is the square of the so-called structure factor, a magnitude which takes into account the effect of all internal interferences due to the geometric phase relationships between all atoms contained in the unit cell. This internal structural effect is:
IF(H) = | F2(H) | = F(H) F*(H)
As a consequence of the complex representation of waves, mentioned at the beginning, the square of a complex magnitude is obtained by multiplying the complex by its conjugate. Thus, specifically, we give the name structure factor, F(H), to the resultant wave from all scattered waves produced by all atoms in a given direction :
F(H) = Σ(1 → n) fj(H) exp [2\(\pi\)(s - s0) rj / λ]
As already stated, the phase differences due to geometric distances R are proportional to (s - s0) R / λ. This means that if we change the origin, the phase differences will be produced according to the geometric changes, in such a way that as the exponential parts of the intensity functions are conjugate complexes, they will affect the intensities in terms of a proportionality constant only. Thus, a change of origin is not relevant to the phenomenon.
In the equation of the total intensity, I(H), the conditions to get a maximum lead to the following consequences:
- The phenomenon of diffraction in crystal samples is discrete, spectral.
- The directions and the periodic repetitions in the reciprocal lattice do not depend on the structure factors. They only depend on the direct lattice. The knowledge of these directions give us the shape and size of the direct unit cell, which actually controls the positions of the diffraction maxima.
- The intensity of the diffraction maxima depends on the structure factor in this direction (at that reciprocal point), which only depend on the atomic distribution within the unit cell. In other words, the diffraction intensities are only controlled by the atomic distribution within the cell. Thus, through the intensities we can obtain information about the atomic structure within the unit cell.
- The total diffraction pattern is the consequence of the diffraction of the different atomic aggregates within the unit cell, sampled in the diffraction points produced by the crystal lattice (the reciprocal points).
- In summary, structural crystallography by X-ray diffraction consists of measuring the intensities of the largest possible amount of diffracted beams in the 3-dimensional diffraction pattern, to get from them the amplitudes of the structure factors, and from these values (through some procedure to allocate the phases for each of these structure factors) to build the electronic distribution in the elementary cell (which can be described in terms of a function whose maxima will give us the atomic positions).

Diffraction patterns of: (a) a single molecule, (b) two molecules, (c) four molecules, (d) a periodically distributed linear array of molecules, (e) two linear arrays of molecules, and (f) a two-dimensional lattice of molecules. Note how the pattern of the latter is the pattern of the molecule sampled in the reciprocal points.
To clarify what has been said above, the reader can analyze further objects and their corresponding diffraction patterns through this link. Additionally we suggest you to watch the video prepared by the Royal Institution to demonstrate optically the basis of diffraction using a wire coil (representing a molecule) and a laser (representing an X-ray beam).
Laue equations, Bragg's interpretation and Ewald's geometric diffraction model
We have seen that the diffraction diagram of a direct lattice defined by three translations, a, b and c, can be expressed in terms of another lattice (the reciprocal lattice) with its reciprocal translations: a*, b* and c*, and these translation vectors (direct and reciprocal) meet the conditions of reciprocity:
a a* = b b* = c c* = 1 and a b* = a c* = b c* = 0
and they also meet that (for instance):
a* = (b x c) / V (x means vectorial or cross product)
where V is the volume of the direct unit cell defined by the 3 vectors of the direct cell, and therefore:
a* = N100 / d100
where N100 is a unit vector perpendicular to the planes of indices h=1, k=0, l=0, and where d100 is the corresponding interplanar spacing. And similarly with b* and c*.
In this way, any vector in the reciprocal lattice will be given by:
H*hkl = h a* + k b* + l c* = Nhkl / dhkl
|H*hkl| dhkl = 1
On the other hand, we have seen that the maxima in the diffraction diagram of a crystal correspond to the maximum function IL(H), meaning that each of the products that define this function must be individually different from zero, as a sufficient condition to obtain a maximum for the diffracted intensity. If we remember that H = (s - s0) / λ, this also means that the three so-called Laue equations must be fulfilled [Max von Laue (1879-1960)]:
H a = h, H b = k, H c = lwhere h, k, l are integers
Laue equations
There is also a less formal way to derive and/or to understand the Laue equations, and therefore we invite interested readers to visit this link ...
These three Laue conditions are met if the vector H represents a vector of the reciprocal lattice, so that:
H = h a* + k b* + l c*
since due to the properties of the reciprocal lattice, it can be stated that:
Hhkl a = h, Hhkl b = k, Hhkl c = l
Said in other words: the three conditions of Laue (Nobel Prize for Physics in 1914) are sufficient to establish that the vector H is a vector of the reciprocal lattice (H =H*hkl).
| H | = 2 sin θhkl / λ = | (s - s0) | / λ = | H*hkl | = 1 / dhkl
And this is Bragg's Law [William L. Bragg (1890-1971)], that can be rewritten in its usual form as:
λ = 2 dhkl sin θhkl
But taking into account that geometrically we can consider spacings of type dhkl/2, dhkl/3, and in general dhkl/n (ie, dnh,nk,nl, where n is an integer), the Bragg’s equation (Nobel Prize in Physics in 1915 ) would be in the form:
λ = 2 (dhkl /n) sin θnh,nk,nl
that is: n λ = 2 dhkl sin θnh,nk,nlwhere n is an integer number
Bragg's Law
There is also a less formal way to derive and/or to understand Bragg's Law, and therefore we invite interested readers to visit this link...
Moreover, if the Laue conditions are fulfilled (as explained in the following figure) all atoms located on the sequence of planes parallel to the one with indices hkl at a given distance (DP) from the origin (DP being an integer multiple of dhkl) will diffract in phase, and their geometric difference-of-phase factor will be:
(s - s0) r = n λ
and consequently a diffraction maximum will be produced in the direction:
s = s0 + λ H*hkl
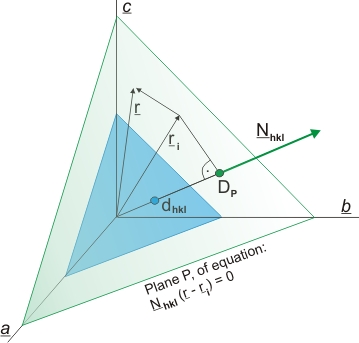
Nhkl = H*hkl dhkl
The plane equation can, therefore, be written as:
H*hkl r = H*hkl ri= |H*hkl| |ri| cos (H*hkl , ri) = (1/dhkl) DP = n
Moreover, this equation holds all the traditional relations of reciprocity of diffraction, between spacing-direction or position-momentum: the shorter spacing, the larger angle and vice versa; direct lattices with large unit cells produce very close diffracted beams, and vice versa.

The figure geometrically describes the direction of the diffraction beam due to the constructive interference between atoms located on the planes with interplanar spacing d(hkl).
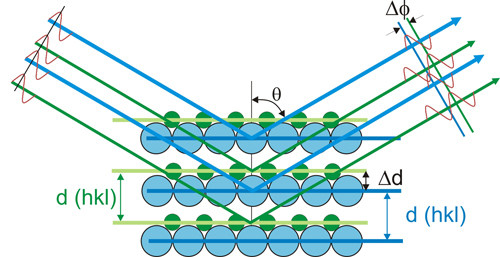
The figure depicts a description of Bragg's model when different types of atoms are located on their respective parallel planes with Δd spacing. The separation between blue and green planes creates interferences and differences of phases (between the reflected beams) giving rise to changes in intensity (depending of the direction). These intensity changes allow us to get information on the structure of atoms that form the crystal).
Readers with installed Java Runtime tools can play with Bragg's model using this applet.
On the other hand, we have seen that, in general:
H = (s - s0) / λ = -s0/λ + s/λand this means that the vectors H can be considered as belonging to a sphere of radius 1/λ centered at a point defined by the vector -s0/λ with respect to the origin where the crystal is. This is known as Ewald's sphere (Ewald, 1921), which provides a very easy geometric interpretation of the directions of the diffracted beams. When the H vectors belong to the reciprocal lattice and the end of the vector (a reciprocal point) lies on that spherical surface, diffracted beams are produced, and obviously the crystal planes are in Bragg's position.
It's amazing how quickly Paul Peter Ewald (1888-1985) developed this interpretation only some months after Max von Laue experiments. His original article, published in 1913 (in German), is available through this link. The advanced reader can also consult the article published by Ewald in Acta Crystallographica (1969) A25, 103-108.

This figure describes Ewald's geometric model. When a reciprocal point , P*(hkl), touches the surface of Ewald's sphere, a diffracted beam is produced starting in the centre of the sphere and passing through the point P*(hkl). Actually the origin of the reciprocal lattice, O*, coincides with the position of the crystal and the diffracted beam will start from this common origin, but being parallel to the one drawn in this figure, exactly as it is depicted in the figure below.

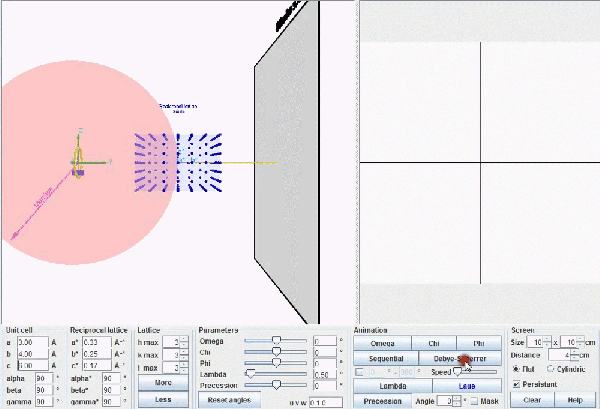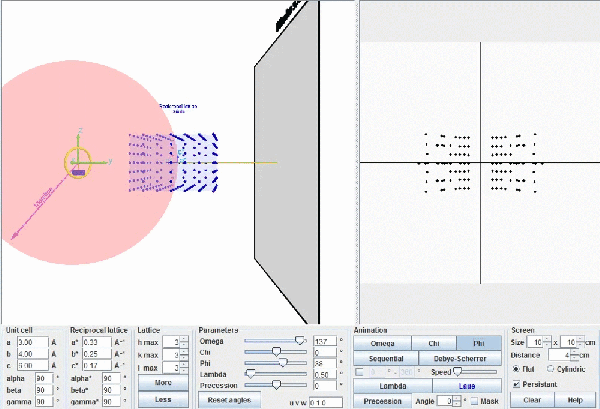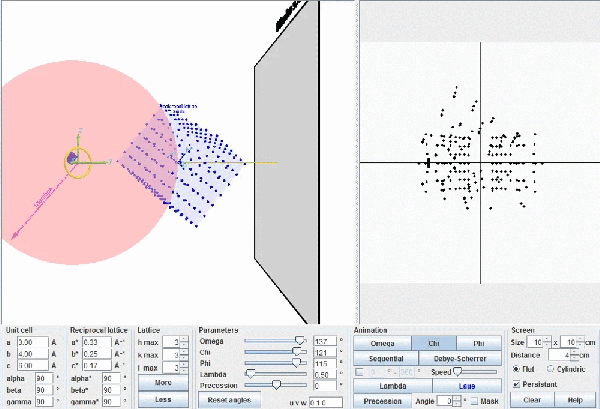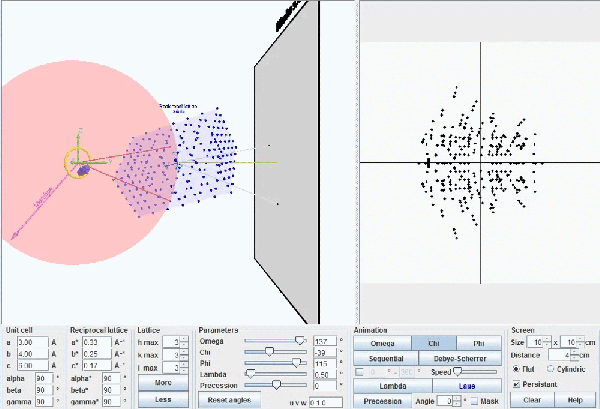
This figure shows the whole reciprocal volume that can give rise to diffracted beams when the sample rotates. Changing the orientation of the reciprocal lattice, one can collect all the beams corresponding to the reciprocal points contained in a sphere of radius 2/λ known as the limit sphere. Reciprocal points are shown as small gray spheres .
To obtain all possible diffracted beams that a sample can provide, using a radiation of wavelength λ, it is sufficient to conveniently orient the crystal and make it turn, so that its reciprocal points will have the opportunity to lay on the surface of Ewald's sphere. In these circumstances, diffracted beams will originate as described above. With larger wavelengths, the volume of the reciprocal space that can be explored will be smaller, but the diffracted beams will appear more separated.

Ewald's model showing how diffraction occurs. The incident X-ray beam, with wavelength λ, shown as a white line, "creates" an imaginary Ewald's sphere of diameter 2/λ (shown in green). The reciprocal lattice (red points) rotate as the crystal rotates, and every time that a reciprocal point cuts the sphere surface a diffracted beam is produced from the center of the sphere (yellow arrows).
According to Bragg's Law, the maximum angle at which one can observe diffraction will correspond to the angle where the sin function is maximum (=1). This also means that the theoretical maximum resolution that can be achieved is λ/2. In practice, due to the decrease of the atomic scattering factors by increasing Bragg angles, appreciable intensities will appear only up to a maximum angular value of θmax < 90º and the real maximum resolution reached will be dmin = λ/2 sin θmax.
Considering that the interplanar spacings dhkl are a characteristic of the sample, by reducing the wavelength, Bragg's Law indicates that the diffraction angles (θ) will decrease; the spectrum shrinks, but on the other hand, more diffraction data will be obtained, and therefore a better structural resolution will be achieved.

According to Ewald's model, the amount of reciprocal space to be measured can be increased by reducing the wavelength, that is, by increasing the radius of the Ewald's sphere
It is also very helpful to visit the pages that on reciprocal space are offered by the University of Cambridge through this link, as well as to look at the video made by www.PhysicsReimagined.com, showing the geometric relationships between direct and reciprocal lattices, displayed below as an animated gif:

Once the foundations of the theoretical model which describe the phenomenon of diffraction are set, we encourage the reader to visit the pages dedicated to the different experimental methods to measure the diffraction intensities.






