2.4: Dynamic Light Scattering
- Page ID
- 55841
Dynamic light scattering (DLS), which is also known as photon correlation spectroscopy (PCS) or quasi-elastic light scattering (QLS), is a spectroscopy method used in the fields of chemistry, biochemistry, and physics to determine the size distribution of particles (polymers, proteins, colloids, etc.) in solution or suspension. In the DLS experiment, normally a laser provides the monochromatic incident light, which impinges onto a solution with small particles in Brownian motion. And then through the Rayleigh scattering process, particles whose sizes are sufficiently small compared to the wavelength of the incident light will diffract the incident light in all direction with different wavelengths and intensities as a function of time. Since the scattering pattern of the light is highly correlated to the size distribution of the analyzed particles, the size-related information of the sample could be then acquired by mathematically processing the spectral characteristics of the scattered light.

Herein a brief introduction of basic theories of DLS will be demonstrated, followed by descriptions and guidance on the instrument itself and the sample preparation and measurement process. Finally, data analysis of the DLS measurement, and the applications of DLS as well as the comparison against other size-determine techniques will be shown and summarized.
DLS Theory
The theory of DLS can be introduced utilizing a model system of spherical particles in solution. According to the Rayleigh scattering (Figure \(\PageIndex{1}\)), when a sample of particles with diameter smaller than the wavelength of the incident light, each particle will diffract the incident light in all directions, while the intensity \(I\) is determined by \ref{1} , where \(I_0\) and \(λ\) is the intensity and wavelength of the unpolarized incident light, \(R\) is the distance to the particle, \(θ\) is the scattering angel, \(n\) is the refractive index of the particle, and \(r\) is the radius of the particle.
\[ I\ =\ I_{0} \frac{1\ +\cos^{2}\theta}{2R^{2}} \left(\frac{2\pi }{\lambda }\right)^{4}\left(\frac{n^{2}\ -\ 1}{n^{2}\ +\ 2}\right)^{2}r^{6} \label{1} \]
If that diffracted light is projected as an image onto a screen, it will generate a “speckle" pattern (Figure \(\PageIndex{2}\) ); the dark areas represent regions where the diffracted light from the particles arrives out of phase interfering destructively and the bright area represent regions where the diffracted light arrives in phase interfering constructively.

In practice, particle samples are normally not stationary but moving randomly due to collisions with solvent molecules as described by the Brownian motion, \ref{2}, where \(\overline{(\Delta x)^{2}} \) is the mean squared displacement in time t, and D is the diffusion constant, which is related to the hydrodynamic radius a of the particle according to the Stokes-Einstein equation, \ref{3} , where kB is Boltzmann constant, T is the temperature, and μ is viscosity of the solution. Importantly, for a system undergoing Brownian motion, small particles should diffuse faster than large ones.
\[ \overline{(\Delta x)^{2}}\ =\ 2\Delta t \label{2} \]
\[D\ =\frac{k_{B}T}{6\pi \mu a} \label{3} \]
As a result of the Brownian motion, the distance between particles is constantly changing and this results in a Doppler shift between the frequency of the incident light and the frequency of the scattered light. Since the distance between particles also affects the phase overlap/interfering of the diffracted light, the brightness and darkness of the spots in the “speckle” pattern will in turn fluctuate in intensity as a function of time when the particles change position with respect to each other. Then, as the rate of these intensity fluctuations depends on how fast the particles are moving (smaller particles diffuse faster), information about the size distribution of particles in the solution could be acquired by processing the fluctuations of the intensity of scattered light. Figure \(\PageIndex{3}\) shows the hypothetical fluctuation of scattering intensity of larger particles and smaller particles.
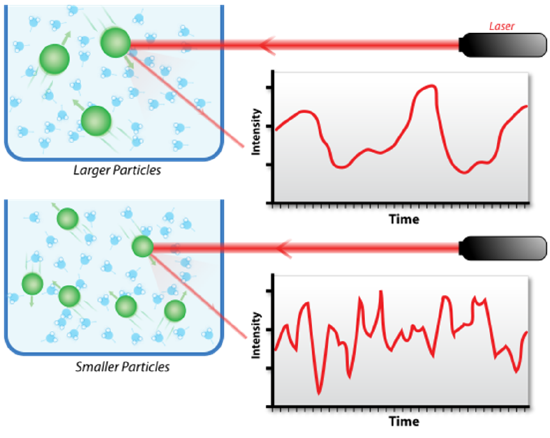
In order to mathematically process the fluctuation of intensity, there are several principles/terms to be understood. First, the intensity correlation function is used to describe the rate of change in scattering intensity by comparing the intensity \(I(t)\) at time \(t\) to the intensity \(I(t + τ)\) at a later time \((t + τ)\), and is quantified and normalized by \ref{4} and \ref{5}, where braces indicate averaging over \(t\).
\[ G_{2} ( \tau ) =\ \langle I(t)I(t\ +\ \tau)\rangle \label{4} \]
\[g_{2}(\tau )=\frac{\langle I(t)I(t\ +\ \tau)\rangle}{\langle I(t)\rangle ^{2}} \label{5} \]
Second, since it is not possible to know how each particle moves from the fluctuation, the electric field correlation function is instead used to correlate the motion of the particles relative to each other, and is defined by \ref{6} and \ref{7} , where E(t) and E(t + τ) are the scattered electric fields at times t and t+ τ.
\[ G_{1}(\tau ) =\ \langle E(t)E(t\ +\ \tau )\rangle \label{6} \]
\[g_{1}(\tau ) = \frac{\langle E(t)E(t\ +\ \tau)\rangle}{\langle E(t) E(t)\rangle} \label{7} \]
For a monodisperse system undergoing Brownian motion, g1(τ) will decay exponentially with a decay rate Γ which is related by Brownian motion to the diffusivity by \ref{8} , \ref{9} , and \ref{10} , where q is the magnitude of the scattering wave vector and q2 reflects the distance the particle travels, n is the refraction index of the solution and θ is angle at which the detector is located.
\[ g_{1}(\tau )=\ e^{- \Gamma \tau} \label{8} \]
\[ \Gamma \ =\ -Dq^{2} \label{9} \]
\[ q = \frac{4\pi n}{\lambda } \sin\frac{\Theta }{2} \label{10} \]
For a polydisperse system however, g1(τ) can no longer be represented as a single exponential decay and must be represented as a intensity-weighed integral over a distribution of decay rates \(G(Γ)\) by \ref{11} where G(Γ) is normalized, \ref{12} .
\[ g_{1}(\tau )= \int ^{\infty}_{0} G(\Gamma )e^{-\Gamma \tau} d\Gamma \label{11} \]
\[ \int ^{\infty}_{0} G(\Gamma ) d\Gamma\ =\ 1 \label{12} \]
Third, the two correlation functions above can be equated using the Seigert relationship based on the principles of Gaussian random processes (which the scattering light usually is), and can be expressed as \ref{13} , where β is a factor that depends on the experimental geometry, and B is the long-time value of g2(τ), which is referred to as the baseline and is normally equal to 1. Figure \(\PageIndex{4}\) shows the decay of g2(τ) for small size sample and large size sample.
\[ g_{2}(\tau ) =\ B\ +\ \beta [g_{1}(\tau )]^{2} \label{13} \]
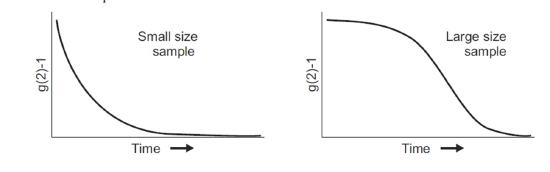
When determining the size of particles in solution using DLS, g2(τ) is calculated based on the time-dependent scattering intensity, and is converted through the Seigert relationship to g1(τ) which usually is an exponential decay or a sum of exponential decays. The decay rate Γ is then mathematically determined (will be discussed in section ) from the g1(τ) curve, and the value of diffusion constant D and hydrodynamic radius a can be easily calculated afterwards.
Experimental
Instrument of DLS
In a typical DLS experiment, light from a laser passes through a polarizer to define the polarization of the incident beam and then shines on the scattering medium. When the sizes of the analyzed particles are sufficiently small compared to the wavelength of the incident light, the incident light will scatters in all directions known as the Rayleigh scattering. The scattered light then passes through an analyzer, which selects a given polarization and finally enters a detector, where the position of the detector defines the scattering angle θ. In addition, the intersection of the incident beam and the beam intercepted by the detector defines a scattering region of volume V. As for the detector used in these experiments, a phototube is normally used whose dc output is proportional to the intensity of the scattered light beam. Figure \(\PageIndex{5}\) shows a schematic representation of the light-scattering experiment.
In modern DLS experiments, the scattered light spectral distribution is also measured. In these cases, a photomultiplier is the main detector, but the pre- and postphotomultiplier systems differ depending on the frequency change of the scattered light. The three different methods used are filter (f > 1 MHz), homodyne (f > 10 GHz), and heterodyne methods (f < 1 MHz), as schematically illustrated in Figure \(\PageIndex{6}\). Note that that homodyne and heterodyne methods use no monochromator of “filter” between the scattering cell and the photomultiplier, and optical mixing techniques are used for heterodyne method. shows the schematic illustration of the various techniques used in light-scattering experiments.
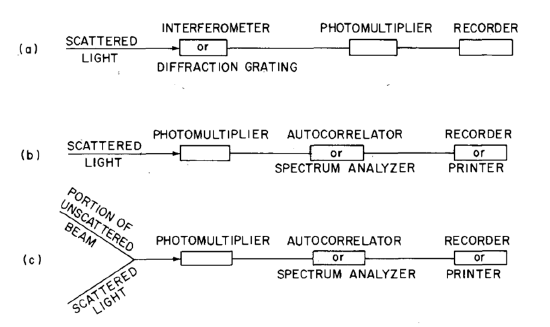
As for an actual DLS instrument, take the Zetasizer Nano (Malvern Instruments Ltd.) as an example (Figure \(\PageIndex{7}\)), it actually looks like nothing other than a big box, with components of power supply, optical unit (light source and detector), computer connection, sample holder, and accessories. The detailed procedure of how to use the DLS instrument will be introduced afterwards.

Sample Preparation
Although different DLS instruments may have different analysis ranges, we are usually looking at particles with a size range of nm to μm in solution. For several kinds of samples, DLS can give results with rather high confidence, such as monodisperse suspensions of unaggregated nanoparticles that have radius > 20 nm, or polydisperse nanoparticle solutions or stable solutions of aggregated nanoparticles that have radius in the 100 - 300 nm range with a polydispersity index of 0.3 or below. For other more challenging samples such as solutions containing large aggregates, bimodal solutions, very dilute samples, very small nanoparticles, heterogeneous samples, or unknown samples, the results given by DLS could not be really reliable, and one must be aware of the strengths and weaknesses of this analytical technique.
Then, for the sample preparation procedure, one important question is how much materials should be submit, or what is the optimal concentration of the solution. Generally, when doing the DLS measurement, it is important to submit enough amount of material in order to obtain sufficient signal, but if the sample is overly concentrated, then light scattered by one particle might be again scattered by another (known as multiple scattering), and make the data processing less accurate. An ideal sample submission for DLS analysis has a volume of 1 – 2 mL and is sufficiently concentrated as to have strong color hues, or opaqueness/turbidity in the case of a white or black sample. Alternatively, 100 - 200 μL of highly concentrated sample can be diluted to 1 mL or analyzed in a low-volume microcuvette.
In order to get high quality DLS data, there are also other issues to be concerned with. First is to minimize particulate contaminants, as it is common for a single particle contaminant to scatter a million times more than a suspended nanoparticle, by using ultra high purity water or solvents, extensively rinsing pipettes and containers, and sealing sample tightly. Second is to filter the sample through a 0.2 or 0.45 μm filter to get away of the visible particulates within the sample solution. Third is to avoid probe sonication to prevent the particulates ejected from the sonication tip, and use the bath sonication in stead.
Measurement
Now that the sample is readily prepared and put into the sample holder of the instrument, the next step is to actually do the DLS measurement. Generally the DLS instrument will be provided with software that can help you to do the measurement rather easily, but it is still worthwhile to understand the important parameters used during the measurement.
Firstly, the laser light source with an appropriate wavelength should be selected. As for the Zetasizer Nano series (Malvern Instruments Ltd.), either a 633 nm “red” laser or a 532 nm “green” laser is available. One should keep in mind that the 633 nm laser is least suitable for blue samples, while the 532 nm laser is least suitable for red samples, since otherwise the sample will just absorb a large portion of the incident light.
Then, for the measurement itself, one has to select the appropriate stabilization time and the duration time. Normally, longer striation/duration time can results in more stable signal with less noises, but the time cost should also be considered. Another important parameter is the temperature of the sample, as many DLS instruments are equipped with the temperature-controllable sample holders, one can actually measure the size distribution of the data at different temperature, and get extra information about the thermal stability of the sample analyzed.
Next, as is used in the calculation of particle size from the light scattering data, the viscosity and refraction index of the solution are also needed. Normally, for solutions with low concentration, the viscosity and refraction index of the solvent/water could be used as an approximation.
Finally, to get data with better reliability, the DLS measurement on the same sample will normally be conducted multiple times, which can help eliminate unexpected results and also provide additional error bar of the size distribution data.
Data Analysis
Although size distribution data could be readily acquired from the software of the DLS instrument, it is still worthwhile to know about the details about the data analysis process.
Cumulant method
As is mentioned in the Theory portion above, the decay rate Γ is mathematically determined from the g1(τ) curve; if the sample solution is monodispersed, g1(τ) could be regard as a single exponential decay function e-Γτ, and the decay rate Γ can be in turn easily calculated. However, in most of the practical cases, the sample solution is always polydispersed, g1(τ) will be the sum of many single exponential decay functions with different decay rates, and then it becomes significantly difficult to conduct the fitting process.
There are however, a few methods developed to meet this mathematical challenge: linear fit and cumulant expansion for mono-modal distribution, exponential sampling and CONTIN regularization for non-monomodal distribution. Among all these approaches, cumulant expansion is most common method and will be illustrated in detail in this section.
Generally, the cumulant expansion method is based on two relations: one between g1(τ) and the moment-generating function of the distribution, and one between the logarithm of g1(τ) and the cumulant-generating function of the distribution.
To start with, the form of g1(τ) is equivalent to the definition of the moment-generating function M(-τ, Γ) of the distribution G(Γ), \ref{14} .
\[ g_{1}(\tau ) =\ \int _{0}^{\infty} G(\Gamma )e^{- \Gamma \tau} d\Gamma \ =\ M(-\tau ,\Gamma) \label{14} \]
The mth moment of the distribution \(mm(Γ)\) is given by the mth derivative of M(-τ, Γ) with respect to τ, \ref{15} .
\[ m_{m}(\Gamma )=\ \int ^{\infty}_{0} G(\Gamma )\Gamma^{m} e^{-\Gamma \tau} d\Gamma \mid_{- \tau = 0} \label{15} \]
Similarly, the logarithm of g1(τ) is equivalent to the definition of the cumulant-generating function K(-τ, Γ), EQ, and the mth cumulant of the distribution km(Γ) is given by the mth derivative of K(-τ, Γ) with respect to τ, \ref{16} and \ref{17} .
\[ ln\ g_{1}(\tau )= ln\ M(-\tau ,\Gamma)\ =\ K(-\tau , \Gamma) \label{16} \]
\[ k_{m}(\Gamma )=\frac{d^{m}K(-\tau , \Gamma )}{d(-\tau )^{m} } \mid_{-\tau = 0} \label{17} \]
By making use of that the cumulants, except for the first, are invariant under a change of origin, the km(Γ) could be rewritten in terms of the moments about the mean as \ref{18} , \ref{19} , \ref{20} , and \ref{21} where here μm are the moments about the mean, defined as given in \ref{22} .
\[ \begin{align} k_{1}(\tau ) &=\ \int _{0}^{\infty} G(\Gamma )\Gamma d\Gamma = \bar{\Gamma } \label{18} \\[4pt] k_{2}(\tau ) &=\ \mu _{2} \label{19} \\[4pt] k_{3}(\tau ) &=\ \mu _{3} \label{20} \\[4pt] k_{4}(\tau ) &=\ \mu _{4} - 3\mu ^{2}_{2} \cdots \label{21} \end{align} \]
\[ \mu_{m}\ =\ \int _{0}^{\infty} G(\Gamma )(\Gamma \ -\ \bar{\Gamma})^{m} d\Gamma \label{22} \]
Based on the Taylor expansion of K(-τ, Γ) about τ = 0, the logarithm of g1(τ) is given as \ref{23} .
\[ ln\ g_{1}(\tau )=\ K(-\tau , \Gamma )=\ -\bar{\Gamma} \tau \ +\frac{k_{2}}{2!}\tau ^{2}\ -\frac{k_{3}}{3!}\tau^{3}\ +\frac{k_{4}}{4!}\tau^{4} \cdots \label{23} \]
Importantly, if look back at the Seigert relationship in the logarithmic form, \ref{24} .
\[ ln(g_{2}(\tau )-B)=ln\beta \ +\ 2ln\ g_{1}(\tau ) \label{24} \]
The measured data of g2(τ) could be fitted with the parameters of km using the relationship of \ref{25} , where \(\bar{\Gamma }\) (k1), k2, and k3 describes the average, variance, and skewness (or asymmetry) of the decay rates of the distribution, and polydispersity index \(\gamma \ =\ \frac{k_{2}}{\bar{\Gamma}^{2}} \) is used to indicate the width of the distribution. And parameters beyond k3 are seldom used to prevent overfitting the data. Finally, the size distribution can be easily calculated from the decay rate distribution as described in theory section previously. Figure \(\PageIndex{6}\) shows an example of data fitting using the cumulant method.
\[ ln(g_{2}(\tau )-B)=] ln\beta \ +\ 2(-\bar{\Gamma} \tau \ +\frac{k_{2}}{2!}\tau^{2}\ -\frac{k_{3}}{3!}\tau^{3} \cdots ) \label{25} \]
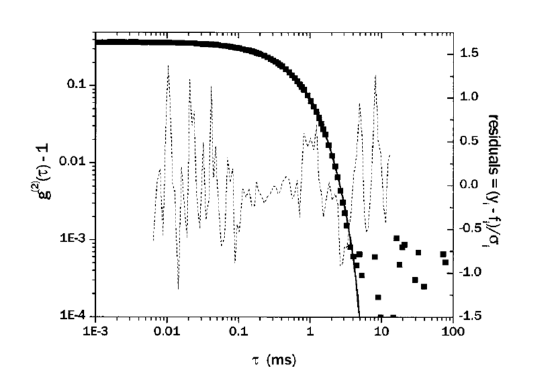
When using the cumulant expansion method however, one should keep in mind that it is only suitable for monomodal distributions (Gaussian-like distribution centered about the mean), and for non-monomodal distributions, other methods like exponential sampling and CONTIN regularization should be applied instead.
Three Index of Size Distribution
Now that the size distribution is able to be acquired from the fluctuation data of the scattered light using cumulant expansion or other methods, it is worthwhile to understand the three kinds of distribution index usually used in size analysis: number weighted distribution, volume weighted distribution, and intensity weighted distribution.
First of all, based on all the theories discussed above, it should be clear that the size distribution given by DLS experiments is the intensity weighted distribution, as it is always the intensity of the scattering that is being analyzed. So for intensity weighted distribution, the contribution of each particle is related to the intensity of light scattered by that particle. For example, using Rayleigh approximation, the relative contribution for very small particles will be proportional to a6.
For number weighted distribution, given by image analysis as an example, each particle is given equal weighting irrespective of its size, which means proportional to a0. This index is most useful where the absolute number of particles is important, or where high resolution (particle by particle) is required.
For volume weighted distribution, given by laser diffraction as an example, the contribution of each particle is related to the volume of that particle, which is proportional to a3. This is often extremely useful from a commercial perspective as the distribution represents the composition of the sample in terms of its volume/mass, and therefore its potential money value.
When comparing particle size data for the same sample represented using different distribution index, it is important to know that the results could be very different from number weighted distribution to intensity weighted distribution. This is clearly illustrated in the example below (Figure \(\PageIndex{9}\) ), for a sample consisting of equal numbers of particles with diameters of 5 nm and 50 nm. The number weighted distribution gives equal weighting to both types of particles, emphasizing the presence of the finer 5 nm particles, whereas the intensity weighted distribution has a signal one million times higher for the coarser 50 nm particles. The volume weighted distribution is intermediate between the two.
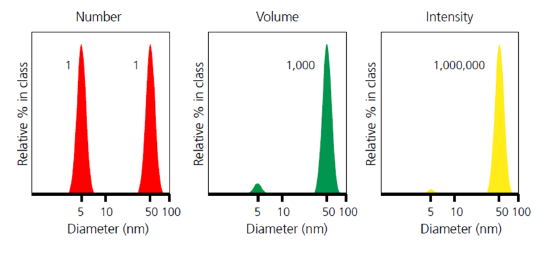
Furthermore, based on the different orders of correlation between the particle contribution and the particle size a, it is possible to convert particle size data from one type of distribution to another type of distribution, and that is also why the DLS software can also give size distributions in three different forms (number, volume, and intensity), where the first two kinds are actually deducted from the raw data of intensity weighted distribution.
An Example of an Application
As the DLS method could be used in many areas towards size distribution such as polymers, proteins, metal nanoparticles, or carbon nanomaterials, here gives an example about the application of DLS in size-controlled synthesis of monodisperse gold nanoparticles.
The size and size distribution of gold particles are controlled by subtle variation of the structure of the polymer, which is used to stabilize the gold nanoparticles during the reaction. These variations include monomer type, polymer molecular weight, end-group hydrophobicity, end-group denticity, and polymer concentration; a total number of 88 different trials have been conducted based on these variations. By using the DLS method, the authors are able to determine the gold particle size distribution for all these trials rather easily, and the correlation between polymer structure and particle size can also be plotted without further processing the data. Although other sizing techniques such as UV-V spectroscopy and TEM are also used in this paper, it is the DLS measurement that provides a much easier and reliable approach towards the size distribution analysis.
Comparison with TEM and AFM
Since DLS is not the only method available to determine the size distribution of particles, it is also necessary to compare DLS with the other common-used general sizing techniques, especially TEM and AFM.
First of all, it has to be made clear that both TEM and AFM measure particles that are deposited on a substrate (Cu grid for TEM, mica for AFM), while DLS measures particles that are dispersed in a solution. In this way, DLS will be measuring the bulk phase properties and give a more comprehensive information about the size distribution of the sample. And for AFM or TEM, it is very common that a relatively small sampling area is analyzed, and the size distribution on the sampling area may not be the same as the size distribution of the original sample depending on how the particles are deposited.
On the other hand however, for DLS, the calculating process is highly dependent on the mathematical and physical assumptions and models, which is, monomodal distribution (cumulant method) and spherical shape for the particles, the results could be inaccurate when analyzing non-monomodal distributions or non-spherical particles. Yet, since the size determining process for AFM or TEM is nothing more than measuring the size from the image and then using the statistic, these two methods can provide much more reliable data when dealing with “irregular” samples.
Another important issue to consider is the time cost and complication of size measurement. Generally speaking, the DLS measurement should be a much easier technique, which requires less operation time and also cheaper equipment. And it could be really troublesome to analysis the size distribution data coming out from TEM or AFM images without specially programmed software.
In addition, there are some special issues to consider when choosing size analysis techniques. For example, if the originally sample is already on a substrate (synthesized by the CVD method), or the particles could not be stably dispersed within solution, apparently the DLS method is not suitable. Also, when the particles tend to have a similar imaging contrast against the substrate (carbon nanomaterials on TEM grid), or tend to self-assemble and aggregate on the surface of the substrate, the DLS approach might be a better choice.
In general research work however, the best way to do size distribution analysis is to combine these analyzing methods, and get complimentary information from different aspects. One thing to keep in mind, since the DLS actually measures the hydrodynamic radius of the particles, the size from DLS measurement is always larger than the size from AFM or TEM measurement. As a conclusion, the comparison between DLS and AFM/TEM is shown in Table \(\PageIndex{1}\).
| DLS | AFM/TEM | |
|---|---|---|
| Sample Preparation | Solution | Substrate |
| Measurement | Easy | Difficult |
| Sampling | Bulk | Small area |
| Shape of Particles | Sphere | No Requirement |
| Polydispersity | Low | No Requirement |
| Size Range | nm to um | nm to um |
| Size Info. | Hydrodynamic radius | Physical size |
Conclusion
In general, relying on the fluctuating Rayleigh scattering of small particles that randomly moves in solution, DLS is a very useful and rapid technique used in the size distribution of particles in the fields of physics, chemistry, and bio-chemistry, especially for monomodally dispersed spherical particles, and by combining with other techniques such as AFM and TEM, a comprehensive understanding of the size distribution of the analyte can be readily acquired.


