Symmetry and Vibrational Spectra (Worksheet)
- Page ID
- 126982
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Learning Objectives
- To use symmetry to find point groups
- To use character tables to predict how many vibrational modes should appear in the IR and Raman Spectra
- Be able to identify the symmetry elements in a compound
- Be able to identify the point group of a molecule
- Use the character table for a point group to predict vibrational spectra
An understanding of symmetry allows us to understand the bonding and physical properties of the compounds we are studying. Symmetry can be used to predict the nature of molecular orbitals and to predict both the electronic and vibration spectroscopic modes for a given molecule. We will begin with molecular symmetry, then find the appropriate point groups which will indicate the character tables available for the molecules and ultimately the the active vibrational modes.
PART I - SYMMETRY
Axes of Rotation – Cn where n is how many times the angle you turn the molecule can be divided into 360°. BF3 has a C3 and three C2’s. The axis with the highest value is the principle axis and will help define the point group.
$$n = \frac{360}{\text{angle of rotation}}\]

Mirror Planes – s this is a reflection through a plane within the molecule. There are three types, vertical (\(\sigma_{v}\)) which contains (“parallel”) the principle rotation axis, horizontal (\(\sigma_{h}\)) which is perpendicular to the principle axis and dihedral (\(\sigma_{d}\)) which contains the principle rotation axis but lies between C2’s that are perpendicular to the principle axis.
XeF4 has examples of all three types of mirror planes. The sh contains all of the atoms, the \(\sigma_{v}\) contains the F on ones side the Xe in the center and the F on the other. A \(\sigma_{d}\) contains only the Xe and reflects the F’s on both sides (as shown in the wedges diagram, this would be perpendicular to this paper).
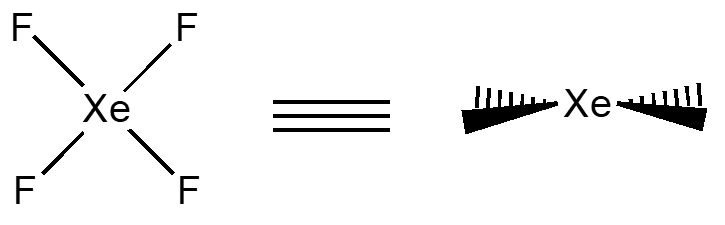
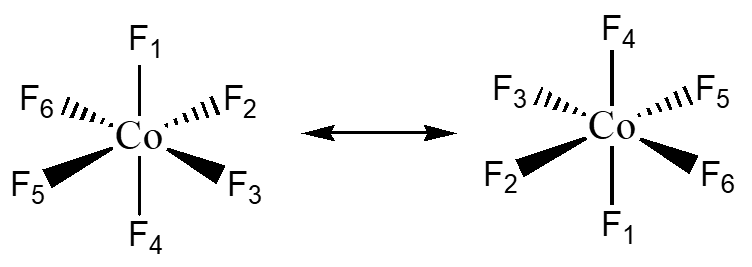
Center of Inversion – i this allows for the molecule to be turned “inside out” through a single point.
CoF6 has a center of inversion through the Co atom. Notice how the top and bottom F’s change position.
Improper Rotation Axis – Sn This is a rotation followed by a reflection through a mirror plane perpendicular to the axis. CCl4 has an S4.

Identity – E do nothing. For some molecules this will be the only symmetry element present.
Key Questions
- BF3 has 3 C2’s what elements are contained in the C2’s? Are they parallel or perpendicular to the principle axis?
- How many C2’s are there in XeF4?
- Define in your own words, the three mirror planes.
- Indicate one example of each of the three planes using XeF4 as an example.
- Using ethylene as an example, prove to yourself that a C2 is not the same as a center of inversion.
- Prove that BF3 has an improper rotation axis, indicate what the symbol should be for that molecule.
- Find the symmetry elements present for each of the following. BCl2F, CCl3Br, PtCl3Br (square planar), PtCl4 (square planar), trans-1,2-dibromo-1,2-dichloroethylene.
- Download SymmetryApp.jar and the library from Blackboard and check your answers to #7. Note, you may need to put in dummy atoms to check some operations.
PART II – Point Groups
All of the symmetry operations for a particular molecule can be grouped together into point groups. These symbols allow us to be more specific about the geometry of a molecule. It eliminates controversial names such as “see saw” and they allow us to use character tables to better understand bonding as well as electronic and vibrational spectra. Later this semester we will use this to understand more fully Molecular Orbital Theory.
Once you understand how to pick out symmetry elements for molecules you can start to use the following flowchart to determine the point groups of your molecules.
Note
This is a beginner’s crutch, you will need to do this without the chart for exams and if you plan to take the GRE subject exam in Chemistry.
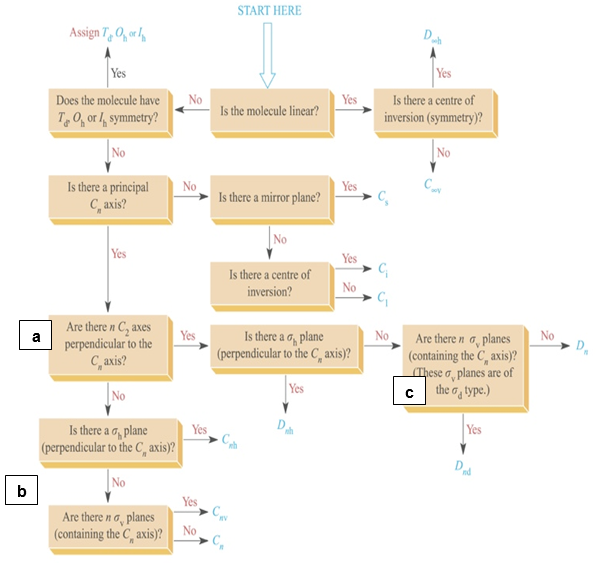
Example \(\PageIndex{1}\):
Find the Point Group for Water.
So starting at the first question….
Water is not linear and it is not one of the special groups Td, Oh or Ih.
It does have a principle rotation axis, a C2 that bisects the HOH angle.
It does not have any perpendicular C2’s and it does not have a sh.
Yes it does have a sv, one that contains the framework and the other that is perpendicular to the page and contains the O and reflects the H’s.
Therefore, the Point group for water is C2v
Key Questions
- For all of the molecules in #7 in Part I, assign point groups.
- In the boxes marked a, b and c on the flow chart, does the n mean that they molecules must have n number of those symmetry elements? Don’t look it up, rather deduce it by looking at different molecules that answer yes at those three boxes. (ie find a molecule with Cnv symmetry to answer the question at a and b and Dnd to answer the question at c). Use the SymmetryApp to help.
Part III - Character Tables for Point Groups
The complete set of symmetry operations for any point group is listed in a matrix called a Character Table. Let’s look at the character table for the C2v point group. Remember water has C2v symmetry.
| C2v | E | C2 | \(\sigma_{v}\) (xz) | \(\sigma'_{v}\) (yz) | ||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | -1 | -1 | Rz | xy |
| B1 | 1 | -1 | 1 | -1 | x, Ry | xz |
| B2 | 1 | -1 | -1 | 1 | y, Rx | yz |
Across the top of the table, notice the symmetry element symbols, if there are multiple elements present (i.e. 2C2’s) then a 2 would appear before the symbol to indicate the number of operations in that class. The order for the point group is the sum of the total number of operations (here it would be 4) Underneath C2v there are representations for the effect that each operation has on mathematical operations. The values in the boxes that cross (for example box E;A1 has a value of 1) are called characters. Characters indicate the effect of the symmetry operation on a given representation.
Key Question
- For the D4d point group, list the symmetry elements present, the number of each operation in that class, the representations and find the order.
Part IV - Spectroscopy
The boxes without a column heading at the end of the table are the spectroscopy active components. The indicate the Microwave (Rxyz), the IR (xyz) and the Raman (xy, yz, xz, x2, y2, z2) active representations. These change from point group to point group. We can use character tables and point groups to find the vibrational modes present for each molecule and predict the number of peaks in the IR and Raman spectra.
To be IR active a molecule must have a change in dipole moment during a vibration, for a molecule to be Raman active a molecule must have a change in polarizability. Both techniques are measuring the change in the molecule when it aborbs light of a specific frequency. The number of modes for IR can be calculated by calculating the degrees of freedom using the formula 3N-6 for non-linear molecules and 3n-5 for linear molecules where N is the number of atoms. Using character tables and group theory we can better understand what atoms and vibrations correspond to the degrees of freedom calculated.
How to find the IR active and Raman Active Modes using point groups
- Find the point group of the molecule and the character table.
- Determine the Reducible Representation, \(\Gamma\) for the molecule. (what atoms move when you carry out the operations times the vector contribution)
- Determine the Irreducible Representation. (use the following equation) $$N_{x} = \frac{1}{Order} \Sigma [ (\# \; \text{of operations in class}) \times (\Gamma) \times (\text{character of x})]$$
- Determine the number of IR active modes (x, y, z) and Raman active modes (quadratic functions of x, y, z in other words (xy, yz, xz, x2, y2, z2, or their combinations x2-y2)
Example \(\PageIndex{2}\):
- Water has C2v symmetry.
- To find \(\Gamma\) we must consider the overall vector geometry for each atom. We can simplify this by doing this in two steps (a) consider which atoms are effected and then (b) consider the vectors associated with the xyz coordinate.
Atom
If an atom is unchanged, then it is given a value of 1, if it is moved a 0.
For Water:
- E operation leaves all atoms in place therefore it has a character of 3 (1 for each atom times 3 for 3 atoms)
- C2 only the O is left unmoved therefore it will have a character of 1.
- \(\sigma_{v}\) that contains the framework, it will be 3 as no atoms move
- \(\sigma_{v}\) that is perpendicular to the framework of atoms, it will be 1 as both H’s move but the O is unchanged.
Vectors
For each atom, we need to figure out how the Cartesian coordinate will change. So the next thing to consider is how xyz moves for each operation. Just consider one of the atoms that move for this. If the vector is unchanged, +1 if it is reversed -1.
For Water:
- E – no change on the xyz therefore E has the value 3
- C2 only the H’s move and here the x and y turn into their negatives -2 and the z remains unchanged +1 so overall, it is a -1
- \(\sigma_{v}\) that contains the framework, one axis becomes negative while the other two remain the same overall +1
- \(\sigma_{v}\) that is perpendicular to the framework of atoms, one axis becomes negative while the other two remain the same overall +1
So now we can tabulate the number of unshifted atoms for each operation in the point group and the vector contributions per atom, multiplying them yields \(\Gamma\).
| E | C2 | \(\sigma_{v(xz)}\) | \(\sigma_{v(yz)}\) | |
|---|---|---|---|---|
| Unshifted atoms | 3 | 1 | 1 | 3 |
| Vector Contribution | 3 | -1 | -1 | 1 |
| \(\Gamma\) | 9 | -1 | 1 | 3 |
- Once we have \(\Gamma\) we can find the Irreducible representations for each representation using the equation
$$N_{x} = \frac{1}{Order} \Sigma [ (\# \; \text{of operations in class}) \times (\Gamma) \times (\text{character of x})]\]
$$\begin{split} N_{A_{1}} &= \frac{1}{4} [(1)(9)(1)] + [(1)(-1)(1)] + [(1)(1)(1)] + [(1)(3)(1)] = 3 \\ N_{A_{2}} &= \frac{1}{4} [(1)(9)(1)] + [(1)(-1)(1)] + [(1)(1)(-1)] + [(1)(3)(-1)] = 1 \\ N_{B_{1}} &= \frac{1}{4} [(1)(9)(1)] + [(1)(-1)(-1)] + [(1)(1)(1)] + [(1)(3)(-1)] = 2 \\ N_{B_{2}} &= \frac{1}{4} [(1)(9)(1)] + [(1)(-1)(-1)] + [(1)(1)(-1)] + [(1)(3)(1)] = 3 \end{split}\]
So the Irreducible representation is 3 A1 + A2 + 2B1 + 3 B2
- At this point we need to subtract the translational and the rotational motions which are found from the x, y, z and the Rx, Ry and Rz symmetry functions. Subtraction yields: 2A1 + B2 so for water we would expect three absorptions in the IR (three modes).
Key Questions
- Calculate the degrees of freedom for the water molecule.
- For XeF4, calculate the degrees of freedom expected.
- Use the water example as a guide and find the representations for the IR active modes for XeF4.
- What would change if we were only looking at the bonding in a molecule?
Reference
- Kelley J. Donaghy, SUNY-ESF


