Slater’s Rules and Periodicity (Worksheet)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Learning Objectives

• Understand the connection between effective nuclear charge and ionization energy, electron affinity and observed electronic configuration
• Be able to calculate effective nuclear charge using Slater’s Rules
• Be able to draw conclusions between effective nuclear charge and atomic radii, ionization energy, and electron affinity
• Use effective nuclear charge to predict and explain the trends associated with atomic radii, ionization energy and electron affinity

While quantum mechanics help us to understand the probability of finding electrons within the atom, they do not fully explain the observed reactivities of these electrons. For example, why does the 4s shell fill before the 3d? Why is the ionization energy of Li much less than that of Cl? To understand this, we need to look more closely at the nuclear/electron relationship. The question is, what effect if any do electrons between the nucleus and the electron of interest have on its reactivity and placement? Slater¹, Clementi and Raimondi² have studied this problem in detail and have found that effective nuclear charge (\(Z_{eff}\)) can be used to estimate atomic radii, ionization energy, electron affinity and to explain observed electron configuration. Clementi and Raimondi use self-consistent field theory to get fairly accurate estimates of \(Z_{eff}\). Slater, however developed a set of rules that allows for a “quick and dirty” assessment of nuclear charge. A basic understanding of these Slater’s Rules will help us understand periodicity and the nuclear/electron relationship better. The following model states Slater’s rules and shows an example of how they can be used.

\[Z_{eff} = Z-S \label{1}\]

where \(Z\) = nuclear charge (atomic number) and \(S\) = screening (shielding) constant

Slater's Rules To calculate \(S\):

1. Write out the electronic configuration of the element in the following order and groupings:

(1s) (2s 2p) (3s, 3p) (3d) (4s, 4p) (4d), (4f), (5s, 5p)….etc….

2. Electrons higher than the one of interest contribute nothing to \(S\).
3. Calculating \(S\) for a particular electron in an ns or np orbital
   1. Electrons in the same (ns,np) grouping contribute 0.35 to \(S\)
   2. Each of the electrons in the (n - 1) energy level contribute 0.85 to \(S\)
   3. Each of the electrons in the (n - 2 or lower) energy levels contribute 1.00 to \(S\)
4. Calculating \(S\) for a particular electron in an nd or nf orbital
   1. Electrons in the same (nd, nf) group contribute 0.35 to \(S\)
   2. Electrons in all of the lower groups contribute 1.00 to \(S\)

Example \(\PageIndex{1}\):

What is the \(Z_{eff}\) for a 2p electron in F?

Solution

Step 1: Write out the electronic configuration of the element

• Electron configuration for F: 1s²2s²2p⁵
• Slater’s Groupings: (1s)² (2s 2p)⁷

Step 2: Calculating \(S\) for a particular electron in an ns or np orbital

$$S = (6 * 0.35) + (2 * 0.85) = 3.8 \nonumber\]

Use Equation \ref{1}

$$Z_{eff} = 9 – 3.8 = 5.2 \nonumber\]

Key Questions

1. (a) As you progress inward from the electron in question, does the shielding influence (contribution to S) of the electrons from nuclear charge get larger or smaller?
   (b) Is this what you would have expected? Why or why not?
2. When you are calculating the \(Z_{eff}\) do you include the electron you are investigating in your calculation of the shielding constant (S)?
3. Using Slater’s rules, calculate the \(Z_{eff}\) for the 2p electron for a Cl atom.
   1. Is this larger or smaller than the \(Z_{eff}\) calculated for F in the model?
   2. What conclusions can you draw between atomic radii and \(Z_{eff}\) (use your previous knowledge of atomic radii here).
4. Equally distribute the atoms of the second period amongst your group and calculate the \(Z_{eff}\) for the outermost valence electron for each. Using these and your argument from 3b, predict the trend you would expect for the atomic radii as you progress from left to right (Li to Ne). Does this agree with your previous knowledge of atomic radii?
5. Using the \(Z_{eff}\) you calculated for all of the atoms in the second period in #4, explain the following graph of ionization energy as a function of atomic number.

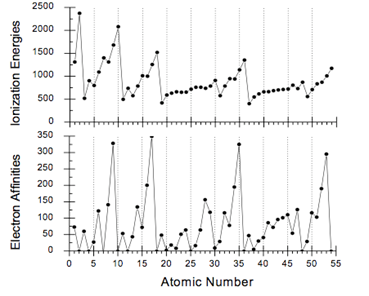
6. Does \(Z_{eff}\) help to explain the deviation from the expected rise in electron affinity between elements 14 and 15 illustrated in the graph above? What else might be involved? Explain.

Exercise \(\PageIndex{1}\)

1. How is the energy of an ns atomic orbital affected by an increase in n?
2. Calculate the \(Z_{eff}\) for a 4s electron and a 3d electron for Vanadium. Based on these numbers explain why the electron configuration for V⁺ ion is more likely to be 3d³4s¹ rather than 3d²4s².
3. Plot the total ionization energies of Alⁿ⁺ as a function of n from n=1 to n=8. Explain the source of discontinuity (if any) in your curve. (Be sure to use a reliable source for the ionization energies and to reference it.) Calculate the \(Z_{eff}\) of Alⁿ⁺ and plot these as a function of n. Are there any conclusions that can be drawn by comparing the two curves?
4. For the ns electrons in Group 1, which is stronger, electron-electron repulsion or nuclear-electron attraction? For the np electrons in Group 7, which is stronger, electron-electron repulsion or nuclear-electron attraction?

References

1. Slater, J. C. Phys. Rev. 1930, 36, 57
2. Clementi E., Raimondi, D.L. J. Chem. Phys. 1963, 38, 2686-2689.

Contributors and Attributions

• Kelley J. Donaghy, SUNY-ESF