Skip to main content
Chemistry LibreTexts

Properties of Octahedral Coordination Compounds (Worksheet)

  1. Last updated
  2. Save as PDF
  • Page ID
    127046

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Name: ______________________________

    Section: _____________________________

    Student ID#:__________________________

    Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

    Learning Objectives

    • Identify metal ions that are able to form high- and low-spin complexes and predict which one will form based on the type of ligand and number of unpaired electrons
    • Predict magnetic properties
    • Indicate understanding of the reasons for Jahn-Teller distortions
    • Identify complexes likely to exhibit Jahn-Teller distortions

    The unique properties of coordination compounds are responsible for their often striking colors, reactivities, and their many applications. The most common stereochemistry of transition metal complexes is octahedral, with six ligands arranged around a central metal ion or atom.

    High- and low-spin complexes

    Information: Ligand field stabilization energy (LFSE) is a comparison of the energies of the d-electrons in a transition metal ion complex to the energies in the uncomplexed metal ion. LFSE for an octahedral complex may be calculated from:

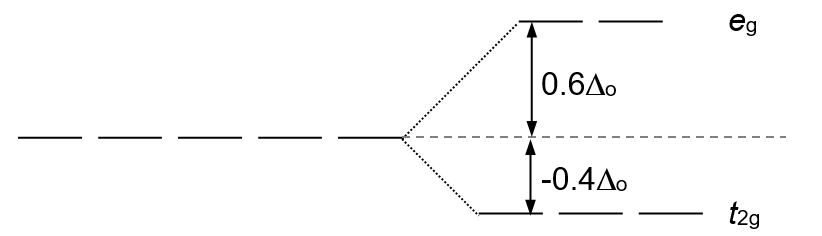
    e81c9050dd284626ff430fa4d39b95c21.png

    \[LFSE = (-0.4x + 0.6y) \Delta_{0}\]

    where x is the number of electrons in the t2g orbitals and y is the number of electrons in the eg orbitals

    Four factors affect the magnitude of the splitting parameter (\(\Delta_{0}\)):

    1. The identity of the metal: \(\Delta_{0}\) is approximately 50% larger for 4d metals compared to 3d and 25% larger for 5d metals compared to 4d.
    2. The oxidation state: higher oxidation states generally have greater crystal field splitting.
    3. The number of ligands: octahedral splitting (\(\Delta_{0}\)) is generally much greater than tetrahedral splitting (\(\Delta_{T}\)).
    4. The nature of the ligands: the spectrochemical series arranges ligands in order of decreasing energy of transitions that occur when they are present in a complex:
    CO>CN->C6H5->CH3->NO2->bpy, NH3>NCS->H2O>O2-, ox>urea, OH->F-, N3->Cl->SCN->S2->Br->I-
    Strong field (large \(\Delta\)) Weak field (small \(\Delta\))
    \(\pi\) acceptors \(\pi\) donors

    Model 1: Cr2+ has 4 d electrons. [Cr(H2O)6]2+ has the ground-state configuration t2g3eg1 (high spin) whereas [Cr(CN)6]4- has the ground-state configuration t2g4 (low spin).

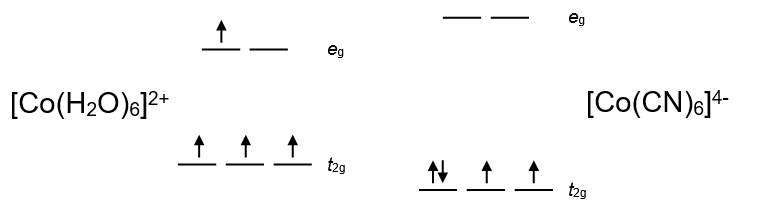
    e8824e7cfd834eb5f7b41789df3af2b02.png

    The high spin configuration (left) has the highest number of parallel spins. Where high spin and low spin complexes are both possible, weak field ligands tend to form high spin configurations because the electron pairing energy (P) is greater than the splitting (\(\Delta_{0}\)). Strong field ligands form low spin complexes because P is less than \(\Delta_{0}\).

    Critical Thinking Questions

    1. For which d electron configurations (d0, d1, d2, d3, d4, d5, d6, d7, d8, d9, d10) are both high spin and low spin configurations possible? (Hint: draw the orbital splitting diagrams)
    2. Would you expect the following complexes to be high-spin or low-spin? Sketch the d-orbital filling patterns for each. [Fe(CN)6]4-, [FeCl6]3+, [Cr(H2O)6]3+, [Co(NO2)6]4-
    3. Identify the number of unpaired electrons in each of the following complexes: [RhF6]3-, [Fe(H2O)6]3+, [Cu(H2O)6]2+, [Cr(CN)6]4-
    4. Calculate LFSE for each complex in CTQ 2 and 3.

    Magnetism

    Model 2: Diamagnetic compounds have all electrons paired and are repelled by a magnetic field. Paramagnetic compounds have unpaired electrons and are attracted by a magnetic field. Magnetometry can be used to distinguish the two. The equation for the magnetic moment is:

    $$\mu_{s + L} = g \sqrt{[S(S+1)]+\bigg[\frac{1}{4}L(L+1)\bigg]}\]

    where \(\mu\) = magnetic moment, g = gyromagnetic ratio (for Bohr magnetons, g = 2.00023, frequently rounded to 2), S = spin quantum number = sum of ms, and L = orbital quantum number = sum of m\(\ell\).

    For most transition metal complexes, any orbital contribution is small and so consideration of the spin-only moment is sufficient:

    $$\begin{split} \mu_{s} &= g \sqrt{S(S+1)} \\ &= 2 \sqrt{S(S+1)} \\ &= \sqrt{4S(S+1)} \end{split}\]

    Because \(S = \frac{1}{2}, 1, \frac{3}{2}, \ldots,\) for n = unpaired electrons = 1, 2, 3, ..., we can write:

    $$\mu_{s}=\sqrt{n(n+2)}\]

    The magnetic properties of coordination compounds give indirect evidence for the electronic configuration and orbital energy levels.

    Critical Thinking Questions

    1. Confirm that \(\sqrt{4S(S+1)}\) and \(\sqrt{n(n+2)}\) are equivalent.
    2. Calculate the spin-only magnetic moment for the following atoms and ions: V3+, Fe3+, Mn2+, Co2+, Ni2+.
    3. Calculate the spin-only magnetic moment for the following complexes: [Co(NH3)6]3+, [RhF6]3-, [Ni(H2O)6]2+, [Cr(H2O)6]2+

    4. Find the number of unpaired electrons, magnetic moment, and ligand field stabilization energy for each of the following complexes: [Co(CO)4], [Cr(CN)6]4-, [Fe(H2O)6]3+

    Jahn-Teller Distortion

    Model 3: The Jahn-Teller theorem states that there cannot be unequal occupation of orbitals with identical energies. For example, d9 ions would have the electron configuration t2g6eg3 with three electrons in the two degenerate eg orbitals without the Jahn-Teller effect. To remove this degeneracy, the complex undergoes elongation or compression along one axis (called a tetragonal distortion):

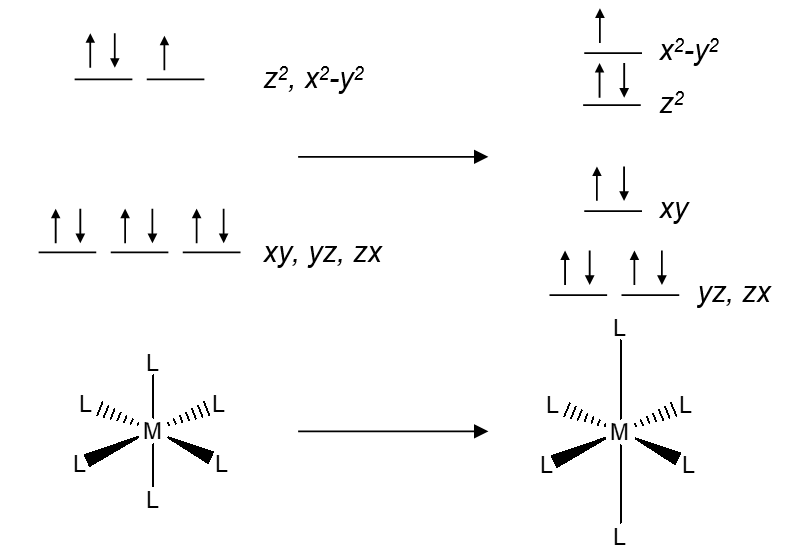
    edc5b0191fda6be2530b343bb77ac3776.png

    Critical Thinking Questions

    1. Identify which d electron configurations (d0 through d10) are likely to exhibit Jahn-Teller distortions when in octahedral complexes (Hint: determine the electron configurations; don’t forget about the high spin and low spin variations!)
    2. Of the first-row transition metals of formula [M(H2O)6]3+, which metals are predicted by the Jahn-Teller theorem to have distorted complexes?
    3. For the following complexes, indicate whether each will show Jahn-Teller distortion and explain your reasoning for each. [Cr(NH3)6]3+, [Cr(H2O)6]2+, [Cr(CN)6]4-, [Ni(NH3)6]2+

    References

    • Jens-Uwe Kuhn, Santa Barbara City College
    • Jessica Martin, Northeastern State University

    Properties of Octahedral Coordination Compounds (Worksheet) is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by LibreTexts.