Molecules – Structure, Symmetry Classification and Properties (Worksheet)

Last updated
Save as PDF

Page ID: 126986

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Learning Objectives

Be able to visualize the 3-dimensional structure of a molecule and classify its point symmetry group.
Be able to predict properties dependent upon symmetry such as dipole moment, presence of enantiomers (chirality) and numbers of chemically equivalent groups.
Ability to visualize the 3-dimensional structure of a molecule and classify its point symmetry group.
Accurate prediction of properties of molecule determined by symmetry considerations.

Symmetry considerations alone can precisely predict properties of a molecule such as whether a permanent dipole moment exists and where it lies on the molecular framework, chirality and groups of chemically equivalent atoms (or nuclei for NMR). Additionally, the number and types of energy states that an atom or molecule can have are rigorously and precisely determined by the symmetry of the molecule or the symmetry of the environment of the atom. Finally, you can know without any quantitative calculations whatever, how many energy states there are and what transitions between them are allowed (for spectroscopic predictions). Symmetry is so powerful, and in this activity you will gain essential practice so that symmetry will start to become a useful tool for you.

Resources

Lecture and web links on our class ANGEL web site.
Plan presented in this activity.
Figures and templates attached to this activity.
Molecular model kits.
Chapter 3 in Rodgers (Glen E. Rodgers, “Descriptive Inorganic, coordination and Solid-State Chemistry,” Brooks/Cole, Thompson Learning, USA, 2002, ISBN 0-12-592060-1).
Origami models from Robert M. Hanson, “Molecular Origami,” University Science Books, Sausalito, California, 1995.

Prerequisites

Understanding the following: symmetry operation; symmetry element; point symmetry group; model building; symmetry classification tree; relation between symmetry and molecular properties

Pre-activity assignment

Bring your assembled model to class.

Plan

Each person in the class will receive an assigned molecule for this activity. Form groups of two to collaborate in the completion of this plan.
Build from a model kit or origami paper template a faithful model of your molecule. Check each other’s molecules for accuracy.
Follow the “decision tree” hand-out to assign the molecule to the appropriate point symmetry group. Then answer the following questions:
1. Does the molecule necessarily have a permanent dipole moment? If so, where does the moment lie on the molecular framework?
2. Is the molecule chiral?
3. How many sets of equivalent atoms exist in this molecule?
Prepare a transparency presenting the molecule, its symmetry classification with the symmetry elements drawn on it, and all parts in question 3 for it.
Have your partner critique the presentation and be ready to present it to the class, using the model to demonstrate the symmetry operations.

Assignments

heptafluorouranate(IV) ion, UF₇^-3 (see sheet)
diborane, B₂H₆ (see sheet)
heptafluoroniobate(V) ion, NbF₇^-2 (see sheet)
Uranyl nitrate ion, UO₂(NO₃)₃^- (see sheet)
octafluorozirconate(IV) ion, ZrF₈^-4 (see sheet)
diiron nonacarbonyl Fe₂(CO)₉ (see sheet)
B(OH)₃ (planar and shaped like a pinwheel)
cis-dichlorotetraamine cobalt (III)
hexaammine cobalt (III) [Co(NH₃)₆]⁺³
trans-dichlorotetraaminecobalt(III)
cisplatin cis-diamminedichloroplatinum(II) (square planar complex)
XeOF₄ (see sheet)
ethane, staggered (see sheet)
SOF₄ (see sheet)

Note

For the molecules designated (see sheet), a paper origami model will be provided in class.

Post activity assignment

Follow through the activity question 3 for NH₂Cl (pyramidal) and [PtCl₄]^-2 (square planar).

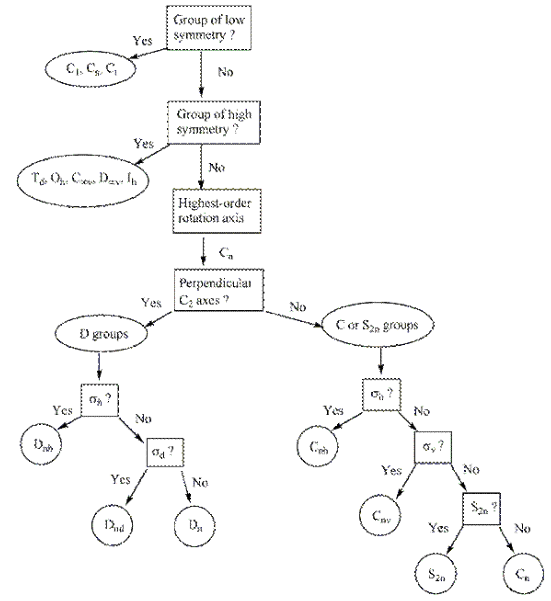
See www.ch.ic.ac.uk/local/symmetry for how to use this flow chart.

Reference

Susan Jackels, Seattle University