13.18: pH and Buffers
- Page ID
- 140120
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The term pH refers to the amount of readily available protons present in the environment. If the environment is water, pH is an index of the concentration of hydronium ion (H3O+) in the water.
pH is related to pKa. Both indices work on a logarithmic scale to avoid carrying large amounts of decimal places in very small numbers. A pH of 6, typical in many biological environments, means that the hydronium ion concentration is about 10-6 moles/L (in which a mole is a unit used for convenient counting of nanoscopic things like molecules or ions, just like a dozen is used for counting eggs or doughnuts).
A low pH actually means there are lots of protons or hydronium ions around. At low pH, the environment is very acidic. Low pH is usually associated with the presence of strong Bronsted acids. The typical pH of about 3 in the stomach is produced by dilute hydrochloric acid, HCl.
A second factor that affects pH is the concentration of species in solution. For example, if a solution of HCl is more concentrated, then clearly more protons will be made available, so the pH will be lower. A solution in which the HCl concentration is 0.1 moles/liter (or 10-1mol/ L) will have a pH of about 1, but a solution in which HCl concentration is 0.001 moles/liter (or 10-3 mol/L) will have pH of about 3. Note that pH is mathematically related to the exponent in the concentration of an acid when written in scientific notation.
Control of pH is very important in biological systems. Many biological processes operate at an optimum pH, and many biomoecules are stable only across a certain pH range. Proteins are particularly sensitive to conditions including pH. Changes in conditions can easily lead to proteins becoming denatured, which means the protein undergoes a shape change that severely affects its ability to function. This shape change is a conformational change, and it is brought about by changing interactions along the protein chain, including changing electrostatic interactions when different sites become protonated or deprotonated.
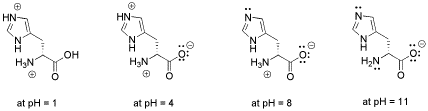
Figure AB18.1. Structure of an amino acid, histidine, at a range of pH values. Note that the overall charge on the amino acid changes with availability of protons.
Different organisms can have different pH ranges over which they function best. Even different tissues within the same organism may work best at different pH values. In order to maintain pH balance at an optimum level, biological systems employ buffers. Buffers are compounds that can either absorb or provide protons in order to keep the pH of their environment from changing. Because they need to absorb or provide protons, buffers are weak Bronsted acids or weak bases, together with their conjugates.
Bicarbonate is an example of a buffer. When pH gets too high, bicarbonate can provide a proton, becoming carbonate.
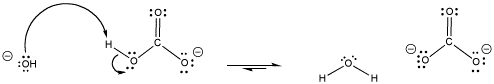
Figure AB18.2. The carbonate / bicarbonate buffer system provides protons.
When pH gets too low, the conjugate base, carbonate, can absorb a proton and become bicarbonate again.
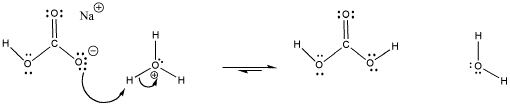
Figure AB18.3. The carbonate / bicarbonate buffer system absorbs protons.
Problem AB18.1.
For the buffer systems described below, use arrows to show how the buffer system would neutralize (i) a hydroxide ion and (ii) a hydronium ion.
a) Ammonia (NH3) / ammonium chloride (NH4Cl)
b) Sodium dihydrogen phosphate (NaO2P(OH)2) / sodium hydrogen phosphate (Na2O3POH)
c) Sodium hydrogen phosphate (Na2O3POH) / sodium phosphate (Na3PO4)
d) Histidine (see above) / histidine hydrochloride (histidine.HCl)
Because the different Bronsted acids involved with these buffers have different pKa's, and so they hold protons more or less tightly, different buffers are able to operate at different pH ranges. This factor, together with control over the concentrations of the components of the buffer system, allows pH to be held fairly constant at almost any value necessary.

