13.17: The Meaning of pKa: Product-to-Reactant Ratio and Equilibrium Constant
- Page ID
- 140119
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The index we have used to assess Bronsted acidity, pKa, is a measurable quantity. It is determined by measuring the ratio of products to reactants in a proton transfer reaction.
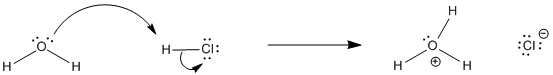
Figure AB17.1. HCl dissolves and ionizes in water.
For example, if HCl is dissolved in water, much of it ionizes, transferring a proton to water to form hydronium ion and chloride anions. The concentrations of all four of these species could be measured and compared. The ratio of products to reactants is called the equilibrium constant, or Keq:
Keq = [H3O+][Cl-] / [H2O][HCl]
The concentrations of these species are generally reported in moles per liter. A mole, you may know, is a unit used to count very large numbers of molecules. Since molecules are very small, we usually deal with very large numbers of them at a time.
By convention, the concentration of water in itself is defined as 1. That leads to a slightly different expression.
Keq' = [H3O+][Cl-] / [HCl]
This ratio, dealing with proton transfer, is also called the acidity constant, Ka.
Ka = [H3O+][Cl-] / [HCl]
Problem AB17.1.
Write the expression for the Ka in each of the following mixtures.
a) HCN in water b) H2S in water c) NH3 in DMSO (DMSO = (CH3)2SO)
The Ka is often a very, very small number or a very, very large one. In the case of HCl in water, the Ka is about 1 x 10-8. Dealing with exponents can be cumbersome. In order to simplify comparisons, the equilibrium constant is expressed logarithmically.
pKa = -logKa
The pKa for HCl transferring a proton to water is -8.
Problem AB17.2.
Convert the following Ka's to pKa's.
a) 1 x 106 b) 1 x 10-9 c) 3.5 x 10-25 d) 8.5 x 1 -17
Problem AB17.3.
Convert the following pKa's to Ka's.
a) -3.5 b) 4.3 c) 9 d) 25
Equilibrium constants are not restricted to proton transfer. They can be used to describe the extent to which any reaction occurs. For example, they can be written for other, reversible processes involving acid-base chemistry.

Figure AB17.2. Equilibrium in the formation of a Lewis acid-base complex between diethyl ether and boron trifluoride.
Lewis acid-base interactions are very often reversible. For example, a Lewis base like ether can donate a pair of electrons to a Lewis acid such as BF3. The ether can take its electrons back again and leave the BF3behind, too. How tightly the ether is held by the BF3 is termed the binding constant. In this case,
Keq = [BF3][Et2O] / [BF3OEt2]
In this case, the equilibrium constant has been reported to be about 0.25.
Problem AB17.4.
What does the equilibrium constant for formation of a complex between BF3 and diethyl ether (above) tell you about the position of the equilibrium?
Problem AB17.5.
The equilibrium constant for complex formation between dimethyl ether (CH3OCH3) and BF3 is 4.2. Compare this value with the one for diethyl ether and explain the difference.
Problem AB17.6.
Write expressions for the binding constant in the following cases.
a) (NH3)2PtCl2 loses an ammonia
b) Mo(CO)6 loses a carbon monoxide
c) FeCl4- loses a chloride anion

