12.6B: Electron Population
- Page ID
- 139316
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Prelude: Populating the Molecular Orbitals
The orbital picture we have described above is really just a potential picture of the electronic structure of dinitrogen (and any other main group or p-block diatomic). We won't get a real picture of dinitrogen's structure until we populate these potential levels with electrons.
- Only the energy levels with electrons have an effect on the energy (and behavior) of the molecule.
In other words, the energy of the electrons determine the behavior of the molecule. The other energy levels are only possibilities that remain unfulfilled.
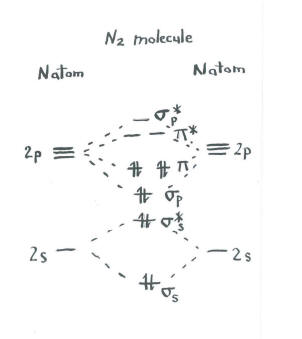
Think about the picture of dinitrogen.
- each nitrogen has five valence electrons.
- there are a total of ten electrons.
- two each go into the s s bonding and s s* antibonding levels. Remember, we kept these separate from the p set as a simplification.
- two each go into the s p bonding and each of the p bonding levels.
The remaining orbitals (s p* antibonding and each of the p* antibonding levels) are unoccupied. These are imaginary levels that do not play a role in determining the energy of dinitrogen. In a real molecular orbital calculation, the electrons in these levels would contribute to the overall energy of the molecule.
We get additional information from this picture. For example, we can see the bond order in dinitrogen.
- Bond order is just the number of bonds between a pair of atoms.
- The bond order is one of several factors that influences the strength of the covalent bond.
- The higher the bond order, the more electrons are shared between the atoms, and the stronger the bond.
In dinitrogen, the s s bonding s s* antibonding levels cancel each other out. One pair is lower in energy than it was in the atom, but the other is higher. There is no net lowering of energy. These electrons do not contribute to a nitrogen-nitrogen bond. These are non-bonding electron pairs.
The six electrons in the s p bonding and the p bonding levels, however, represent a decrease in energy from the energy levels in the free nitrogen atoms. These three, low-energy pairs of electrons indicate three bonds between the nitrogen atoms.
Remember, we have made some short-cuts in this picture, and a real molecular orbital calculation could give slightly different results. Nevertheless, it would still reveal a bond order of three as well as two non-bonding electron pairs.
In addition, sometimes molecular orbital pictures are shown in different ways. A molecular orbital interaction diagram shows how atomic or molecular orbitals combine together to make new orbitals. Sometimes, we may be interested in only the molecular orbital energy levels themselves, and not where they came from. A molecular orbital energy level diagram just shows the energy levels in the molecule. Frequently, but not always, energy level diagrams are shown without any pictures of the orbitals, in order to focus attention on the energy levels, which in a fundamental way are the most important part of the picture. Furthermore, because only the occupied energy levels actually contribute to the energy of the molecule, sometimes the higher-energy, unoccupied orbitals are left out of the picture.

Very often the results of molecular orbital calculations reinforce what we would predict from Lewis structures. If you draw a Lewis structure of dinitrogen, you will also predict a triple nitrogen-nitrogen bond. The chief advantage of molecular orbital theory is that it allows quantitative prediction of energy when we do a real calculation on a computer. In addition, it is important to realize that there is no real reason for the octet rule unless we consider quantum mechanics. Lewis structures are founded on an empirical observation that electrons form pairs and octets, without attempting to explain why. Molecular orbital theory takes some fundamental relationships from physics and applies them to very complicated molecules with very good success. Just by knowing the number of electrons in the molecule, and by knowing approximately where the nuclei are located in the structure, molecular orbital calculations give very useful information about energy. In addition, in more complicated cases than N2, these calculations can even correct our first guess about molecular geometry and where the bonds are located.
Problem MO6.1.
A Molecular Orbital Diagram for a diatomic molecule (two atoms) always has the same basic pattern.
• Draw a picture of the levels.
• Label each level with σ, σ*, π, π*
Problem MO6.2.
A Molecular Orbital Diagram for a diatomic molecule (two atoms) varies in the number of electrons. How do you populate the electrons?
Problem MO6.3.
Construct a qualitative molecular orbital diagram for chlorine, Cl2. Compare the bond order to that seen in the Lewis structure (remember that an electron in an antibonding orbital cancels the stabilization due to bonding of an electron in a bonding orbital).
Problem MO6.4.
- a) Construct a qualitative molecular orbital diagram for oxygen, O2.
- b) Compare the bond order to that seen in the Lewis structure.
- c) How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- d) Compounds that have all of their electrons paired are referred to as diamagnetic. Those with unpaired electrons are referred to as paramagnetic. Paramagnetic materials are attracted by a magnetic field, but diamagnetic things are not. How would you expect molecular oxygen to behave?
Problem MO6.5.
- a) Construct a qualitative molecular orbital diagram for peroxide anion, O22-.
- b) Compare the bond order to that seen in the Lewis structure.
- c) How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- d) Based on molecular orbital pictures, how easily do you think dioxygen could be reduced to peroxide (through the addition of two electrons)?
Problem MO6.6.
Construct a qualitative molecular orbital diagram for diboron, B2. Do you think boron-boron bonds could form easily, based on this picture?
Problem MO6.7.
- a) Construct a qualitative molecular orbital diagram for dicarbon, C2.
- b) Compare the bond order to that seen in the Lewis structure.
- c) How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
Problem MO6.8.
- a) Construct a qualitative molecular orbital diagram for acetylide anion, C22-.
- b) Compare the bond order to that seen in the Lewis structure.
- c) How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- d) Based on molecular orbital pictures, how easily do you think dicarbon could be reduced to acetylide (through the addition of two electrons)?
Problem MO6.9.
Make drawings and notes to summarize the effect of populating antibonding orbitals.
Problem MO6.10.
Researchers at Johns Hopkins recently reported the formation of Na4Al2 in a pulsed arc discharge (they put a lot of electric current through a sample of sodium and aluminum; Xinxing Zhang, Ivan A. Popov, Katie A. Lundell, Haopeng Wang, Chaonan Mu, Wei Wang, Hansgeorg Schnöckel, Alexander I. Boldyrev, Kit H. Bowen, Angewandte Chemie International Edition, 2018, 57(43), 14060-14064. Copyright 2018, John Wiley & Sons. Used with permission.).
- a) The compound is ionic. Explain which atoms form the cations, based on periodic trends.
- b) Therefore, what atoms form the anion?
- c) The anion is one molecule. What is the charge on this molecule?
- d) Show how to calculate the total valence electrons in this molecular anion.
- e) Draw a Lewis structure for this molecular anion.
- f) Construct a diatomic molecular orbital energy level diagram for this molecule. Label the energy levels (sigma, pi etc) and add in the correct number of electrons.
- g) Show how to calculate the bond order in the molecule.


