12.2B: Dihydrogen (Worksheet)
- Page ID
- 139310
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Bonding in the hydrogen molecule
Lewis suggests that two atoms with unpaired electrons may share their electrons to form a bond. In a Lewis structure, we can draw those two electrons between the symbols for the two atoms to show that a bond has formed. Quantum mechanics offers a quantitative mathematical view of molecules, and is considered to give an accurate picture of the behaviour of atoms and molecules. Now, instead of putting two atoms beside each other and letting two dots get together to form a bond, like in a Lewis structure, we'll think about bonding in quantum mechanical terms.
- Two hydrogen atoms are placed next to each other.
- The two atoms are surrounded by the waves formed by their electrons.
- If the two atoms are close together, these two waves overlap in between the two atoms.
What happens when waves overlap? Interference patterns develop. Think of a flat, calm pond, into which you and a friend throw two small stones, a few feet apart. The ripples that result move out in circles from the two points where the stones fell in, and when the two sets of waves meet each other, new patterns result. The circular sets of waves combine to form new waves with new shapes.
When waves meet, there are two basic combinations that result. These combinations depend on whether the two waves are in phase or out of phase with each other.
- If the waves are in phase, so that the peak of one wave lands on top of the peak of another, and the trough of one wave coincides with the trough on the other, constructive interference occurs. The waves add up, and get bigger where they overlap.
- If the waves are exactly out of phase, the peak of one falls into the trough of another, and where they overlap the two waves are canceled out. This is destructive interference.
We can apply these ideas to the electrons in to atoms that come together to make a bond. In Lewis structures, individual electrons on two different atoms are paired up in a bond between the two atoms. The electrons have to be combined to make a bond. If electrons have wave properties, then there will be interference patterns that result when these atoms come together.
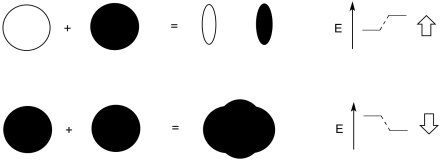
Before we start, note that the waves that we will be dealing with look a little different from the standing waves we looked at before. These waves will be three-dimensional and will occupy different regions of space. Instead of drawing phase information as peaks and troughs, we are going to use a common convention of shading to signify whether we are looking at the positive part (in terms of phase) or the negative part of a wave. For example, we might show the crests in blue and the troughs in red,or we might show one in black and the other in white. In a standing wave, the phases would look like this:

In a hydrogen atom, the electron is found in a spherical area around the nucleus. We won't be able to see two distinct phases - a crest and a trough - in this wave at one time. However, we could look at two different hydrogen atoms and illustrate whether their electrons are in phase or out of phase with each other.

When those two electrons come together and they are in phase with each other, constructive interference occurs. They won't overlap completely; these are atoms and they take up space. However, they will be able to sit pretty close to each other, sort of smushing their electrons together. That constructive intereference will happen in the middles, between the atoms.

When the two electrons come together and they are out of phase, destructive interference occurs. Again, that will happen in the middle, between the atoms.
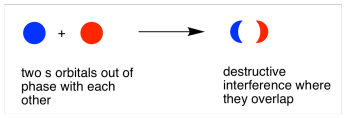
So, in the pair of hydrogen atoms, two waves can combine to produce two possible outcomes.
- In one, the height of the combined wave is highest between the two atoms, where they are overlapping and in phase. The amplitude of the wave is greater here.
- In the other case, the combined wave is composed of two halves that are out of phase, and there is no wave at all between the two atoms, where they have cancelled out; the amplitude of this wave is zero between the two nuclei.
Those two possible combinations produce two different results. We keep track of these outcomes using a molecular orbital interaction diagram. The diagram says that the two orbitals can combine in two different ways: in phase or out of phase. The diagram also tells us that the in-phase combination results in a decrease in energy when the two atoms come together. The out-of-phase combination results in an increase in energy when the atoms come together.

Figure MO2.1. A molecular orbital interaction diagram for H2. A hydrogen atom 1s orbital is shown on the left with its accompanying energy level. The same is shown on the right. In the middle of the diagram, the two hydrogen 1s orbitals can combine in two ways: in phase and out-of-phase. These combinations produce two new orbitals (or electron waveforms) with two new energy levels.
Why does the in-phase combination go down in energy, whereas the out-of-phase combination goes up?
Consider the idea that these waves each have a wavelength, and that this wavelength is related to kinetic energy. For the 1s electron on a hydrogen atom, we can really only visualize half the wave; this half-wave is basically the size of a hydrogen atom, so the total wavelength would be two hydrogen atoms long (for lack of a better yardstick).
For the out-of-phase combination, we can visualize the entire wave, both its "peak" on one side and the "trough" on the other. The two hydrogen atoms are not merely sitting beside each other, they are actually overlapping, so that the distance from one end of the wave to the next is actually somewhat less than two hydrogen atoms. Let's say it's one and a half hydrogen atoms long. This wave has a shorter wavelength than the waves on either individual hydrogen atom, and so it is at higher energy.

Figure MO2.2. A comparison of wavelengths as seen along the bond axis in dihydrogen.
For the in-phase case, again, the two hydrogen atoms are overlapping. But this time we can only visualize half the wave; so the total wavelength would be longer than two hydrogen atoms. Maybe it's three hydrogen atoms long. This wave has a longer wavelength than the electron in an individual hydrogen atom, so it is at lower energy.
- The combination of atomic orbitals results in new, molecular orbitals.
- The number of atomic orbitals combined = the number of molecular orbitals produced.
- In-phase (low energy) and out-of-phase (high energy) combinations are possible.
And now for the weird part:
- According to quantum mechanics, the in phase and out of phase combinations occur simultaneously.
Where would the two electrons actually go? The aufbau process used for atomic electron configurations holds true here. Two electrons can be found in the same space provided they are spin-paired; one would have spin "up" and the other one spin "down". Both electrons could be found in the lower energy orbital. That means both hydrogen electrons go down in energy when H2 forms; the formation of a hydrogen molecule from two hydrogen atoms is thus exothermic.
- The occupied orbital is called a bonding orbital; it is responsible for the bond energy in H2.
- Bond energy refers to the amount of energy given off when a bond forms.
What would happen if each hydrogen atom brought two electrons with it? Would two hydride ions form a bond?
- There would be four electrons in an H22- molecule.
- The first two electrons would occupy the lower, bonding orbital.
- The next two electrons would occupy the upper orbital
- Overall, there would be no net loss of energy, so a bond would not form.
- The out-of-phase combination is called an antibonding orbital, because its increase in energy offsets the decrease in energy that occurs when electrons go into a bonding orbital.
- Placing electrons in an antibonding orbital weakens or breaks a bond.
What does quantum mechanics tell us about bonding that we can't learn from Lewis structures? We learn that electrons can sometimes lower their kinetic energy by forming bonds. If that is the case, the bond will form. On the other hand, if kinetic energy cannot be lowered, the bond won't form at all.
- Covalent bonds form because electrons can adopt longer wavelengths.
- Electrons with longer wavelengths have lower kinetic energy.
Problem MO2.1.
Add a few words to explain the ideas conveyed in these drawings.