Worksheet 6: Solutions and Vapor Pressures
- Page ID
- 78266
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Template:HideTOCWork in groups on these problems. You should try to answer the questions without accessing the Internet.
Q1: Vapor Pressure and Boiling
The vapor pressure of a gas above its own liquid depends on temperature. The boiling point, or temperature at which bubbles of vapor form within a liquid, depends upon both vapor pressure and atmospheric pressure. The following graph shows the vapor pressure curves for two substances A and B
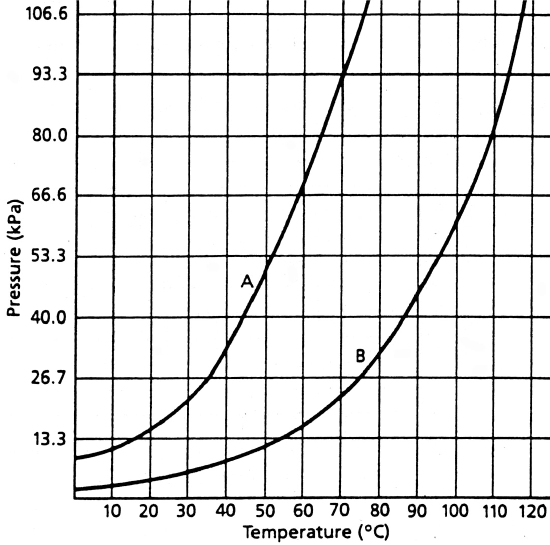
Answer the following questions based on the above graph
- What is the vapor pressure of A at 35°C? __________________
- What is the vapor pressure of B at 35°C? __________________
- At what temperature is the vapor pressure of A 106.6 kPa?. __________________
- What is the vapor pressure of B at this temperature? __________________
- At what temperature is the vapor pressure of B 106.6 kPa? __________________
- What is the “normal” boiling point of A? __________________
- What is the “normal” boiling point of B? __________________
- At what temperature would A boil in Denver where atmospheric pressure is 93.3 kPa? ________________
- What would the atmospheric pressure have to be in order for B to boil at the same temperature as you gave in your answer to #h?. __________________
Q2
The following table shows the vapor pressure of a certain liquid at various temperatures. Graph the data in the table provided.
| Temp °C | Pressure (kPa) | Temp °C | Pressure (kPa) | Temp °C | Pressure (kPa) |
|---|---|---|---|---|---|
| 0 | 1 | 60 | 22 | 120 | 80 |
| 10 | 2 | 70 | 29 | 130 | 93 |
| 20 | 3 | 80 | 37 | 140 | 107 |
| 30 | 7 | 90 | 46 | 150 | 122 |
| 40 | 11 | 100 | 56 | ||
| 50 | 16 | 110 | 68 |

- What effect does rising temperature have on vapor pressure?
- What must be true at the boiling point of a liquid?
- If atmospheric pressure was 96 kPa, what would be the boiling point of the substance whose vapor pressure you graphed?
- What would happen to the boiling point if the atmospheric pressure would begin to rise?
- How would the cooking time of an egg that is to be hard boiled be affected by high altitude? Explain.
Solutions and Vapor Pressure
A pure substance has well-defined physical properties such as freezing and boiling points. In contrast, many properties of a solution depend on the concentration of solute. Properties of solutions that depend on the concentration (but not on the identity) of solute are called colligative (collective) properties. You will learn how the concentration of a solute affects four properties of a solution. As the concentration of solute increases:
- vapor pressure decreases
- boiling point increases
- freezing point decreases
- osmotic pressure increases
We will treat these effects both qualitatively and quantitatively and you will learn why they happen. We will discuss some important applications of these effects.
Volatile vs. non-volatile components of a solution
For each colligative property we will usually consider the case of a non-volatile solute dissolved in a volatile solvent (a typical example is any ionic compound dissolved in water).
A volatile substance is one with a measurable vapor pressure at moderate temperatures. In general, volatility increases as intermolecular forces decrease.
Vapor pressure is the pressure inside a closed container when a liquid is in equilibrium with its own gas phase so the rate of evaporation is equal to the rate of condensation. When a non-volatile solute is dissolved in a volatile solvent, the vapor pressure of the solvent is reduced. As the concentration of the solute increases, the vapor pressure of the solvent decreases.
Q3
Why does the addition of a solute reduce the vapor pressure of a volatile solvent? Entropy is the key! Remember that one of the two driving forces for any process is an increase in entropy. Consider the following two processes occurring in a sealed container at the same temperature.
Process 1: Evaporation of pure water
\[H_2O(l) \rightarrow H_2O(g) \nonumber \]
Process 2: Evaporation of water from a solution
\[H_2O (solution) \rightarrow H_2O(g) \nonumber \]
Clearly the entropy increases in both processes (a gas has more entropy than that substance as a liquid or solution).
- Which process results in a greater increase in the entropy of the system? Explain.
- Which process will result in a higher equilibrium vapor pressure. Explain
Q4
An alternative explanation for vapor pressure reduction is based on this fact: as the concentration of a solute increases, the concentration of the water decreases. Why does a lower water concentration result in a lower vapor pressure?
Raoult’s law
The French chemist Francois-Marie Raoult found that for sufficiently dilute solutions or for solutions with miscible components, the vapor pressure of a solvent over a solution is directly proportional to the mole fraction of the solvent in the solution. Raoult’s law is
\[P_1 = \chi_1P_1^o \nonumber \]
where \(P_1^o\) is the vapor pressure of pure solvent, \(\chi_1\) is the mole fraction of the solvent.
Q5
As the mole fraction of the solute increases, the mole fraction of the solvent _______________ and the vapor pressure of the solvent _______________. (as expected).
Q6
Rewrite Raoult’s law in terms of X2, the mole fraction of the solute.
Q7
According to the equation you just wrote, as the mole fraction of the solute increases, the vapor pressure of the solvent _______________. (as expected).
Q8
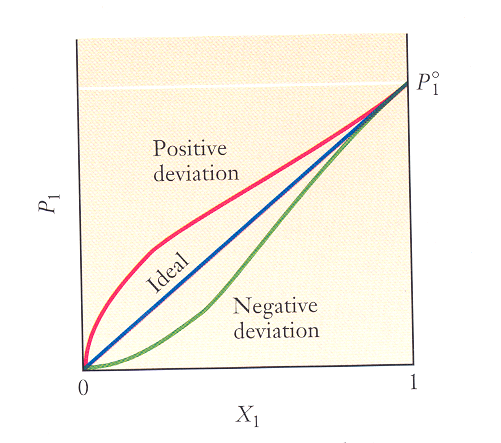
The figure below is a graph of the vapor pressure of the solvent vs. the mole fraction of the solvent for 3 different aqueous solutions. As you move along the x-axis from left to right, is the concentration of the solute increasing or decreasing?
Q9
A solution that obeys Raoult’s law is called an ideal solution (straight line in the graph). Ideal solutions form when the solute and solvent are miscible. (Fill in the blank with greater than, less than, or equal to.)
- In an ideal solution, the strength of the solute-solvent interactions is ____________________ the strengths of the solute-solute interactions and the solvent-solvent interactions.
- The top curve in the graph represents a solution whose vapor pressure is higher than predicted by Raoult’s law. In this case, the strength of the solute-solvent interactions is _____________________ the strengths of the solvent-solvent and solute-solute interactions.
- The bottom curve represents a solution whose vapor pressure is lower than predicted by Raoult’s law. In this case, the strength of the solute-solvent interactions is _____________________ the strengths of the solvent-solvent and solute-solute interactions.
Q10
Notice that all 3 curves converge as X1 approaches 1. Why? (This is why all sufficiently dilute solutions obey Raoult’s law! This should remind you of ideal gases!)
Q11
What is the vapor pressure of water above a solution that is 5% sucrose (by moles) at 50oC? (Vapor pressure table is attached.) Don’t forget that Raoult’s law (as written above) is in terms of the mole fraction of water!
| Temperature (°C) | ||||||||||
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Vapor Pressure (mm Hg) | ||||||||||
| 4.6 | 9.2 | 17.5 | 31.8 | 55.3 | 92.5 | 149.4 | 233.7 | 355.1 | 525.8 | 760 |
Q12
The vapor pressure over a solution of urea (CH4N2O) is 291.2 mm Hg. The vapor pressure of pure water at the same temperature is 355.1 mm Hg. Calculate the mole fraction of urea in the solution. Don’t forget that Raoult’s law (as written above) is in terms of the mole fraction of water!
Q13
Ethanol and water form an ideal solution (they are miscible). Both of these substances are volatile so they both obey Raoult’s law.
- Which is more volatile, ethanol or water? (Think about smell and ease of evaporation.)
- If you have a 1:1 mixture of ethanol and water, which has a higher vapor pressure at 25oC?
- If you took the vapor from above the 1:1 mixture and cooled it down so that the entire vapor phase condensed, you would no longer have a 1:1 mixture. Which would you have more of, ethanol or water?
- This problem describes the process of fractional distillation. Imagine taking the condensate from part c and heating it back to 25oC and repeating the process. After several repetitions, you would have pure ethanol! Distillation is also used aboard ships to purify water from the ocean. In this case, you don’t have to do multiple cycles of evaporation and condensation. Why not?

