Oxidation numbers and Electronic Configurations (Worksheet)
- Page ID
- 14977
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your texook. If you get stuck, try asking another group for help.
The sum of the charges of the metal cation and its ligands adds up to give the charge of the complex ion. If the complex ion is charged, this is balanced by counter ions.
The number of valence electrons on an atom is equal to its group number. In a cation, the oxidation number is equal to the number of these electrons which have been removed. Transition metal cations have a configuration \(d^z\) where \(Z\) is the number of valence electrons left over after ionization:
\[\begin{align*} Z &= \text{number of valence electrons on atom} – \text{charge of cation} \\[4pt] &= \text{group number} – \text{oxidation number} \end{align*} \]
For example:
- Ni is in group 10 so \(\ce{Ni^{2+}}\) has (10 – 2) = 8 valence electrons left: it has a \(d^8\) configuration.
- Cr is in group 6 so \(\ce{Cr^{3+}}\) has (6 – 3) = 3 valence electrons left: it has a \(d^3\) configuration.
Magnetic Properties: To minimize repulsion, electrons occupy orbitals singly before they pair up There are five d-orbitals and, as each orbital can accommodate two electrons, there is space for a maximum of ten electrons. If this process leads to unpaired electrons, the complex is paramagnetic and is attracted towards magnetic field. If there are no unpaired electrons, the complex is diamagnetic and is repelled by magnets.
Q1
- Show the electron configuration for the transition metal cation using the box notation in the table.
- Indicate if the complex is paramagnetic or not in the final column of the table.
- Complete the ‘oxidation number’ column of the table below by working out the oxidation number of each of the transition metal cations.
- Complete the ‘d configuration’ column in the table by working out z for each of the transition metal ions.
This has been completed for the complexes in the first two rows of the table.
| Coordination Compound or Complex | Oxidation Number | d Configuration | Electron Arrangement | Paramagnetic? |
|---|---|---|---|---|
| \(K_2[NiCl_4]\) | +2 | \(d^8\) | Yes | |
| \([Cr(en)_3]Br_3\) | +3 | \(d^3\) | Yes | |
| \(Na[MnO_4]\) | ||||
| \((NH_4)_2[CoCl_4]\) | ||||
| \([Cr(NH_3)_5(H_2O)]Cl_3\) | ||||
| \([Zn(en)2Cl_2]\) | ||||
| \(Pt(NH_3)Cl_2\) |
*en is \(NH_2CH_2CH_2NH_2\) and can bond through lone pairs on both \(N\) atoms (bidentate ligand).
Transferrin
Iron is found in many biological molecules. Typical of its coordination chemistry in fairly recently evolved systems is transferrin, which is used to transport iron in the blood. The Fe(III) atom is bonded to O and N atoms through five ligands: 4 amino acids and 1 carbonate anion (\(CO_3^{2-}\)).
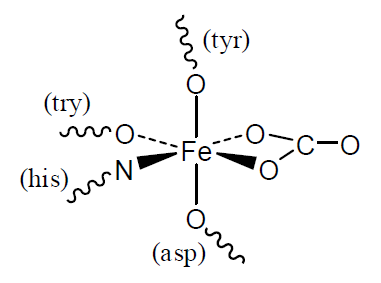
Q2
- How many unpaired electrons will the Fe(III) atom have?
- What is the coordination number and approximate geometry of the Fe(III) atom. Describe how this is achieved with 5 ligands.
- The Fe(III) is released in a cell by a decrease in the pH. Use your knowledge of acid-base chemistry to suggest what the effect of low pH will be on the ligands in the complex.
Ferredoxins
Iron-sulfur clusters are widespread in biology and date further back in evolutionary time. They contain Fe(II) and/or Fe(III) ions coordinated by S atoms, the simplest of which is shown opposite. They are involved in redox reactions in which the oxidation numbers of the iron atoms change.
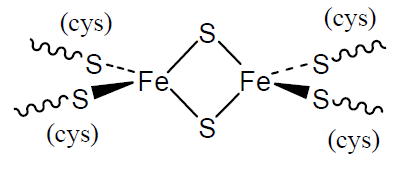
Q3
- What are the coordination numbers and approximate geometries of the Fe atoms?
- How many unpaired electrons will a Fe(II) atom and a Fe(III) atom have?
- Given your answer to Question 2, suggest why magnetic studies indicate no net unpaired electrons when both iron atoms are present as Fe(III) in this cluster.
- Using your answer to Question 3, predict the net number of unpaired electrons in the reduced form containing one Fe(II) and one Fe(III).


