Intermolecular Forces and Interactions (Worksheet)
- Page ID
- 77705
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Template:HideTOCWork in groups on these problems. You should try to answer the questions without accessing the Internet.
Most substances can exist in either gas, liquid, or solid phase under appropriate conditions of temperature and pressure. The phase that we see under ordinary conditions (room temperature and normal atmospheric pressure) is a result of the forces of attraction between molecules or ions comprising the substance. The strength of these attractions also determines what changes in temperature and pressure are needed to effect a phase transition.
Intermolecular Forces
The tendency of a substance to be found in one state or the other under certain conditions is largely a result of the forces of attraction that exist between the particles comprising it. We will concentrate on the forces between molecules in molecular substances, which are called intermolecular forces. (Forces that exist within molecules, such as chemical bonds, are called intramolecular forces.) The greater the strength of the intermolecular forces, the more likely the substance is to be found in a condensed state; i.e., either a liquid or solid. As we have seen, the model of an ideal gas assumes that the gas particles (molecules or atoms) have virtually no forces of attraction between them, are widely separated, and are constantly moving with high velocity and kinetic energy. In truth, there are forces of attraction between the particles, but in a gas the kinetic energy is so high that these cannot effectively bring the particles together. With stronger intermolecular forces or lower kinetic energy, those forces may draw molecules closer together, resulting in a condensed phase.
Electrostatics and Moments of Fixed Charge Distributions
Chemical bonds (e.g., covalent bonding) are intramolecular forces which hold atoms together as molecules. The forces that hold molecules together in the liquid and solid states are called intermolecular forces and are appreciably weaker. Intermolecular forces (IMF) can be qualitatively ranked using Coulomb's Law:
\[V(r) = - \dfrac{q_1q_2}{ 4 \pi \epsilon_o r} \label{Col} \]
where \(q_1\) and \(q_2\) are charges and \(r\) is the distance between them. \(V(r)\) is the Coulombic potential and the Coulombic force between these particles is the negative derivative of the potential:
\[F(r) = - \dfrac{dV(r)}{dr}= \dfrac{q_1q_2}{ 4 \pi \epsilon_o r^2} \label{Force} \]
When \(q_1\) and \(q_2\) have opposite signs, the force is positive (i.e., an attractive interaction). Correspondingly, if \(q_1\) and \(q_2\) have the same sign, then the force is negative (i.e., a repulsive interaction). Three obvious consequences of Equations \(\ref{Col}\) and \(\ref{Force}\) are:
- opposite charges attract,
- the bigger the charges, the stronger the interaction, and
- the closer the charges, the stronger the interaction.
To complicate matters, molecules and atoms have a distribution \(\rho(\vec{r})\) that result from the 3D distribution of charges (both nuclei and especially electrons). \(\rho(\vec{r})\) will describe polarized bonds resulting from the an unequal sharing of electrons between electronegative elements (O, N, halogens) and electronegative atoms. As expected, molecular geometry also plays an important role in determining \(\rho(\vec{r})\) for a molecule. We can do a "multipole expansion" of \(\rho(\vec{r})\) in spherical coordinates in powers of \(1/r^n\). This involves vector calculus and triple integration
\[ M_n = \iiint_V\mathbf r^n \rho(r) \, dV \label{moment} \]
Solving this integral is beyond the scope of Chem 2BH, but the gist is important:
- If n=1, then \(M_1\) is the monopole moment and is just the net charge of the distribution
- If n=2, then \(M_2\) is the dipole moment
- If n=3, then \(M_3\) is the quadrupole moment
- If n=4, then \(M_4\) is the octupole moment
Example: Dipole-dipole forces
Dipole-dipole forces of attraction exist between molecules that are polar – those that have a permanent dipole moment. The polarities of individual molecules tend to align by opposites, drawing the molecules together and thereby favoring a condensed phase.
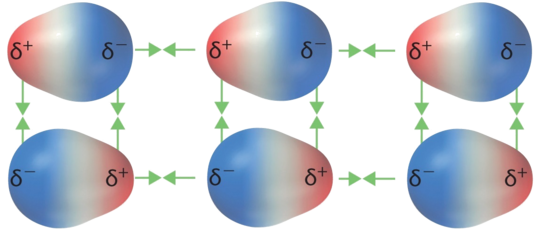
These additional forces of attraction must be overcome in a transition to a less-ordered phase (e.g., solid to liquid, liquid to gas), so substances with dipole-dipole attractions between their molecules tend to have higher melting points and boiling points than comparable compounds composed of nonpolar molecules, which only have London dispersion intermolecular forces.
Permanent - Permanent Charge Distribution IMFs
There are multiple "flavors" of IMF, but they originate from Equation \(\ref{Col}\), but differ in terms of charge distributions. The interaction between two molecules can be decomposed into different combinations of moment-moment interactions. For example: monopole-monopole is a charge-charge interaction (Equation \(\ref{Col}\)), monopole-dipole, dipole-dipole, charge-quadrupole, dipole-quadrupole, quadrupole-quadrupole, charge-octupule, dipole-octupole, quadrupole-octupole, octupole-octople etc.
Often, but not always, these interactions can be ranked in terms of strengths with of interactions involving lower number of moments dominating those with higher moments. However, the relevant moments that is important for the IMF of a specific molecule depend uniquely on that molecules properties. For example, an uncharged molecule will not have a monopole moment and hence will not have monopole-monopole IMF, nor monopole-dipole or monopole-quadrupole IMFs. Similarly, if a molecule does not have a dipole moment nor monopole moment, then quadrupolar interactions will be important.
The hydrogen bonding IMF is a special moment-moment interaction between polar groups when a hydrogen (H) atom covalently bound to a highly electronegative atom such as nitrogen (N), oxygen (O), or fluorine (F) experiences the electrostatic field of another highly electronegative atom nearby.
Permanent - Induced Charge Distribution IMFs
Since electrons in atoms and molecules are dynamic, they can be polarized (i.e., an induced moments that does not exist in absence of permanent charge distribution). Then the same interactions discussed above can occur. Examples include permanent monopole (charge) - induced dipole interaction, permanent dipole - induced dipole interaction, permanent quadrupole-induced dipole interaction etc. The first two interactions are the most relevant for our discussion.
The strength of the induced dipole moment, \(\mu_{induced}\), is directly proportional to the strength of the electric field, \(E\) of the permanent moment with a proportionality constant \(\alpha\) called the polarizability. The strength of the electric field causes the distortion in the molecule.
Instantaneous - Induced Charge Distribution IMFs
The instantaneous unequal sharing of electrons causes rapid polarization and counter-polarization of the electron cloud in atoms and molecules which generate (very) short lived dipole moments. The London IMF (also called dispersion force) is a transient attractive force that results when an Instantaneous dipole on one species then induced a dipole moment on the other. London dispersion forces and dipole-dipole forces are collectively known as van der Waals forces. Molecules can have any mix of these three kinds of intermolecular forces, but all substances at least have London dispersion forces.
London dispersion forces exist for all substances, whether composed of polar or nonpolar molecules. They arise from the formation of temporary, instantaneous polarities across a molecule from circulations of electrons. An instantaneous polarity in one molecule may induce an opposing polarity in an adjacent molecule, resulting in a series of attractive forces among neighboring molecules.
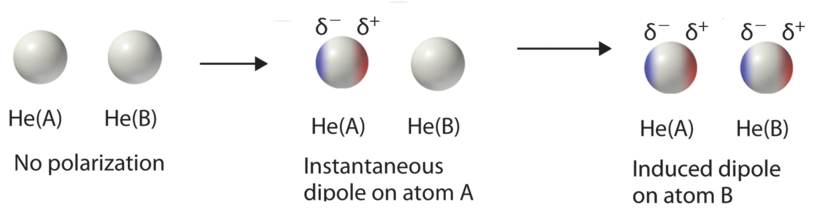
London dispersion forces arise from changing electron distributions. Because all molecules have electrons, all molecular substances have London dispersion forces, regardless of whether they are polar or non-polar. Molecules with higher molecular weights have more electrons, which are generally more loosely held. This makes their electron clouds more deformable from nearby charges, a characteristic called polarizability. As a result, substances with higher molecular weights have higher London dispersion forces and consequently tend to have higher melting points, boiling points, and enthalpies of vaporization. The following data for the diatomic halogens nicely illustrate these trends.
Table \(\PageIndex{1}\): Physical Properties of non-polar Halogens| Element | F2 | Cl2 | Br2 | I2 |
|---|---|---|---|---|
| m.p. (°C) | -220 | -101 | -7.3 | 114 |
| b.p. (°C) | -188 | -34 | 58.8 | 184 |
| At 25 °C | gas | gas | liquid | solid |
Hydrogen Bonding
A hydrogen bond is a non-covalent attraction between a hydrogen that is covalently bonded to a very electronegative atom (X) and another very electronegative atom (Y), most often on an adjacent molecule. (X and Y may be the same or different elements.)
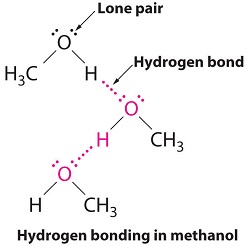
For the most part, only compounds in which hydrogen is covalently bonded to O, N, or F are candidates for hydrogen bonding. Covalent bonds with these elements are very polar, resulting in a partial negative charge (δ–) on the O, N, or F. This partial negative charge can be attracted to the partial positive charge (δ+) of the hydrogen in an X–H bond on an adjacent molecule. Thus, the H×××Y hydrogen bond, unlike the covalent X–H bond, results mainly from electrostatic attraction. Hydrogen bond strengths typically are in the range 4 - 46 kJ/mol, much less than the strengths of typical covalent bonds. Nonetheless, hydrogen bond strength is significantly greater than either London dispersion forces or dipole-dipole forces. Hydrogen bonds in HF(s) and H2O(s) (shown on the next page) are intermediate in strength within this range.
.png?revision=1&size=bestfit&width=640&height=225)
Repulsive Forces
When any molecules are in direct contact a strong repulsion force kicks in. The repulsive force is what prevents two atoms from occupying the same space and if it did not always win (stronger than the attracitve forces above), then all matter would collapse into one huge glob! The universal repulsive force arises directly from two main aspects of quantum theory: the Heisenberg uncertainty principle and the Pauli exclusion principle.
Distance Dependence of Forces
The distance corresponding to the minimum potential energy is known as the equilibrium distance. This is the average distance that will be maintained by the two particles if there are no other forces acting on them, such as might arise from the presence of other particles nearby. A general empirical expression for the potential energy between two particles can be written as
\[V(r) = Ar^{-n} + Br^{-m} \label{7.2.1} \]
\(A\) and \(B\) are proportionality constants and \(n\) and \(m\) are integers. This expression is sometimes referred to as the Mie equation. The first term, \(A\), corresponds to repulsion is always positive, and \(n\) must be larger than \(m\), reflecting the fact that repulsion always dominates at small separations. The \(B\) coefficient is negative for attractive forces, but it will become positive for electrostatic repulsion between like charges. The larger the value of one of these exponents, the closer the particles must come before the force becomes significant. Table \(\PageIndex{1}\) lists the exponents for the types of interactions we will describe in this lesson.
Table \(\PageIndex{2}\) Classification of intermolecular forces|
|
|
n |
|
|---|---|---|---|
| ions | Coulombic | - | 1 |
| ion - polar molecule | ion-dipole | - | 2 |
| two polar molecules | dipole-dipole | - | 3 |
| ion - nonpolar molecule | ion - induced dipole | - | 4 |
| polar and nonpolar molecule | dipole - induced dipole | - | 6 |
| nonpolar molecules | dispersion | - | 6 |
| repulsions | quantum | 9 | - |
Q1
Based on your knowledge of chemicals, rank the IMFs in Table \(\PageIndex{2}\) terms of strongest to weakest.
Q2
Rank the IMFs Table \(\PageIndex{2}\) in terms of shortest range to longest range.
Q3
Identify the strongest intermolecular force present in pure samples of the following substances:
- \(SO_2\)
- \(H_2O\)
- \(CH_2Cl_2\)
- \(SCO\)
- \(PCl_3\)
- \(SO_3\)
Q4
Identify the strongest intermolecular force operating in the condensed phases of the following substances. Fully explain how you determined this.
- \(Cl_2\)
- \(CO\)
- \(SO_2\)
- \(SO_2\)
- \(CH_2Cl_2\)
- \(HF\)
- \(CH_3OCH_3\)
Phases
As we have seen, the model of an ideal gas assumes that the gas particles (molecules or atoms) have virtually no forces of attraction between them, are widely separated, and are constantly moving with high velocity and kinetic energy. In truth, there are forces of attraction between the particles, but in a gas the kinetic energy is so high that these cannot effectively bring the particles together. With stronger intermolecular forces or lower kinetic energy, those forces may draw molecules closer together, resulting in a condensed phase. Going from gas to liquid to solid, molecular velocities and particle separations diminish progressively as structural order increases. In the case of liquids, molecular attractions give rise to viscosity, a resistance to flow. Also, the absence of intermolecular forces above the surface of a liquid results in surface tension, the development of a “skin” on the surface, which causes beading of liquid droplets and also allows light objects to rest on a liquid surface without sinking (e.g., water bugs). Solids have stronger intermolecular forces, making them rigid, with essentially no tendency to flow. Although the mix of types and strengths of intermolecular forces determines the state of a substance under certain conditions, in general most substances can be found in any of the three states under appropriate conditions of temperature and pressure. Changing those conditions can induce a change in the state of the substance, called a phase transition.
Q5
Based on the IMF present in each of the molecules below, predict the relative boiling points of each of the substances below. Arrange each series of substances in order of increasing boiling point. State your reasons for the order you use (identify the forces and explain how they affect the boiling point).
- dimethyl ether (\(CH_3OCH_3\)), ethanol (\(CH_3CH_2OH\)), and propane (\(CH_3CH_2CH_3\))
- \(Br_2\), \(Cl_2\), \(I_2\)
Q6
Give an explanation in terms of IMF for the following differences in boiling point.
- \(HF\) (20° C) and \(HCl\) (-85° C)
- \(CHCl_3\) (61° C) and \(CHBr_3\) (150° C)
- \(Br_2\) (59° C) and \(ICl\) (97° C)
Q7
Indicate which of the following properties will increase, decrease or remain unaffected by an increase in the strength of the intermolecular forces?
- vapor pressure (pressure of gas above a liquid sample in a closed container) decreases with increased intermolecular forces
- normal boiling point (boiling point at 1 atmosphere pressure) increases with increased intermolecular forces
- heat of vaporization (heat requires to take a liquid sample to the gaseous phase) increases with increased intermolecular forces
- surface tension (adhesion of molecules) increases with increased intermolecular forces

