Crystal Field Theory (Worksheet)
- Page ID
- 15733
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Introduction to Crystal field theory
Crystal field theory is one of the simplest models for explaining the structures and properties of transition metal complexes. The theory is based on the electrostatics of the metal-ligand interaction, and so its results are only approximate in cases where the metal-ligand bond is substantially covalent. However, because the model makes effective use of molecular symmetry, it can be surprisingly accurate in describing the magnetism, colors, structure, and relative stability of metal complexes.
Q1: The d-Orbitals
It is necessary to know the d-orbitals by name for this discussion. Below each of the these orbitals identify their name (i.e., \(d_{xy}\), \(d_{x^2y^2}\), \(d_{zy}\), \(d_{z^2}\), \(d_{xz}\),). Pay careful attention to the axis plotted.
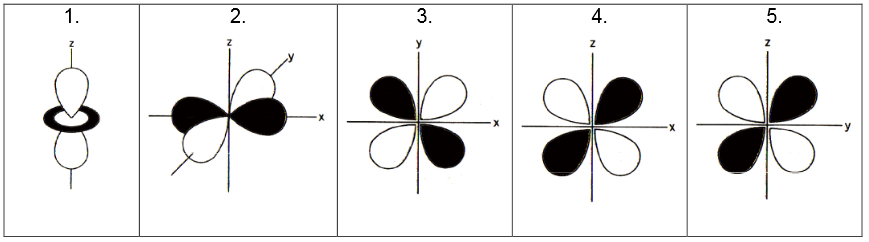
What does the black and white parts of the orbitals below represent?
Q2: The d-Orbital Charge Densities
As you learned previously about orbitals, they are wavefunctions that can be used to describe the spatial density of electron charge in the atom via the orbital squared. For each of the five orbitals above, diagram the corresponding electron density on the 3D axis below. Clearly indicate which orbitals corresponds to which density and label each axis clearly.




Q3: The Ligand Field
Now consider an octahedron complex \(ML_6^m\), where \(m\) is the charge on complex and \(L\) is a monodentate ligand (e.g., the chloro- ligand). On each figure above, sketch an octahedral "ligand field" in3D with six black balls to represent the six ligands. Place one "ligand ball" on one of the axes (e.g., -x, x, -y, y, z and -z). You do not need to draw the transition metal, since the five d-orbitals are attributed to it.
Q4: The Energy Diagram in Absence of Ligand Field
We have routinely sketched the energies of the five \(d\) orbitals in Q1 as five energetically horizontal lines to represent that they are degenerate (same energy). Draw those five horizontal lines to represent the energies of the d-orbitals in the absence of the ligand field.
Q5: The Energy Diagram in Presence of Octahedral Ligand Field (the eg orbitals)
In the octahedral ligand field in Q3, the d-orbitals are no longer equivalent to one another (i.e., the degeneracy is broken). The relative energies of the five orbitals will change. In the first two orbitals shown above (#1 and #2), the lobes are directed towards the ligands. Hence, if the d-orbitals contained electrons (at least \(d^1\)), that electron would “prefer” not being in either of those two orbitals due to electron-electron repulsion. Do you expect the energies connected between the ligand field and the electrons in the orbitals #1 and #2 to be stabilized (lower in energy) or be destabilized (higher in energy) based on your drawing of Figure Q2? Explain why in terms of electron-electron electrostatics. We call these two orbitals the \(e_g\) orbitals.
Q6: The Energy Diagram in Presence of Octahedral Ligand Field (the t2g orbitals)
Do the other three orbitals (#3 – #5) offer a better alternative to the first two in terms of reduced electron (from the d-orbital) – electron repulsion? That is, do you expect the ligand field and electrons in orbitals #3 - #5 to be stabilized or destablized. Why? We call these three orbitals the \(t_{2g}\) orbitals.
Q7: Energy Splitting
In Box (a) below, sketch an energy diagram with the five d-orbitals all having the same energy — as they would if no ligands were present. To the right of that, sketch the relative energies of the five d-orbitals with an octahedral field of ligands present. Hint: The three d-orbitals 3 – 5 all behave the same; they are energetically degenerate. The other two are also energetically degenerate among the two of them. While this isn’t obvious by looking at the diversely different structures of each, they do have the same symmetry and the same n and l quantum numbers so thus, they transform the same.The split energy pattern you have created is called a crystal field splitting. Add symmetry labels (\(t_{2g}\) and \(e_g\)) to the two sets of orbitals in the “split energy” picture shown at right (use lower case).
Q8: Populating the Energy Diagram for \(Ti^{+3}\)
- What is the electron configuration of the \(\ce{Ti^{+3}}\) ion?
- How many d-electrons does the \(\ce{Ti^{+3}}\) ion have?
The energy diagrams drawn in Question 7 describes the energies of the deflections in an octahedral ligand field. These non-degenerate orbitals are filled following the same Aufbau rules discussed before (e.g., Pauli Exclusion Principle and Hund Rule). Now, consider a complex of Ti(III) in an octahedral ligand field, sketch the crystal field splitting pattern (energy diagram) and populate it with number of electrons that the Ti(III) has. Label each orbital with the \(t_{2g}\) or \(e_g\) symmetry designation.

Q9: Symmetry Nomenclature for d-electron Configurations
The d-electron configuration is sometimes written as
(symmetry term, lower energy)# of electrons (symmetry term upper energy level)# of electrons
For example, a d3-ion in such an octahedral ligand field would be written as \((t_{2g})^3(e_g)^0\). Rewrite the electron configuration of Ti(III) using the correct symmetry terms (ask TA or instructor for help with this).
Q10
- Consider a complex of Ti(II) in an octahedral ligand field, sketch the crystal field splitting pattern (energy diagram) in panel (a) and populate it with number of electrons that the Ti(II) has. Label each orbital with the \(t_{2g}\) or \(e_g\) symmetry designation.
- Consider a complex of V(II) in an octahedral ligand field, sketch the crystal field splitting pattern (energy diagram) in panel (b) and populate it with number of electrons that the V(II) has. Label each orbital with the \(t_{2g}\) or \(e_g\) symmetry designation.

Q11: Crystal Field Splitting
The splitting between the lower energy levels and the upper energy orbitals is called the crystal field splitting and is abbreviated \(\Delta_o\) for the octahedral complex. Label \(\Delta_o\) on the energy diagrams for Quesiton Q7, Q8, and Q10.
Q12: Adding Energies (Advanced, skip if needed)
Determine the exact fraction of the energy difference between the lower energies and the average energy (that is, what is the energy of an electron in the lowest orbital after splitting compared to before the ligand split the originals). Label the fraction on the energy diagram. Do the same for the orbitals of higher energy. The two fractions should add up to 1.
Q13: Octahedral Splitting Parameter (Advanced, skip if needed)
The exact magnitude of \(\Delta_o\) depends on several factors that we will discuss later. All we need to know for now is that \(\Delta_o\) varies. The two fractions written on the energy diagram above should be multiplied by \(\Delta_o\). Do that now by writing the fractions \(x \Delta_o\) on the energy diagram above.
Q14: Crystal Field Stabilization Energy (Advanced, skip if needed)
When one electron occupies one of the lower energy levels, it has been stabilized (compared to the average energy of all five orbitals by one the x (fraction) x Δo. This is called the crystal field stabilization energy (CFSE) and is positive because of the name “stabilization energy.” The change in energy is negative and simply given by
\[ΔE = -\text{CFSE}. \nonumber \]
Thus, electronic structures with electrons in the lower energy levels and not the upper energy levels have a positive CFSE and have \(ΔE < 0\). Calculate the CFSE for \(d^1\), \(d^2\) and \(d^3\) in an octahedral ligands field.
Q15: Crystal Field Stabilization Energy (CFSE) (Advanced, skip if needed)
When we get to \(d^4\), the 4th electron can either occupy one of the lower energy orbitals or one of the higher energy orbitals. If it occupies the lower level, it also is stabilized by the same amount as the first three were, however, now there is a “pairing energy” that offsets the additional CFSE somewhat. The “pairing energy” is the energy it costs when two electrons share the same orbital. The pairing energy is abbreviated “P.” If \(P > Δ_o\), the electron will prefer to occupy which orbital? Both scenarios are possible.
- If \(P > Δ_o\), the electron will prefer to occupy which orbitals and why?
- If \(P < Δ_o\), the electron will prefer to occupy which orbitals and why?
Q16: Low Spin vs. High Spin Configurations
When the electrons choose to occupy the higher energy orbitals rather than pairing up, the situation is called high-spin because the number of unpaired electron is maximized. When they pair up, the situation is called low-spin. High/low-spin possibilities only occur for a few d-electron configurations. What are they?
Q17: The Full Row
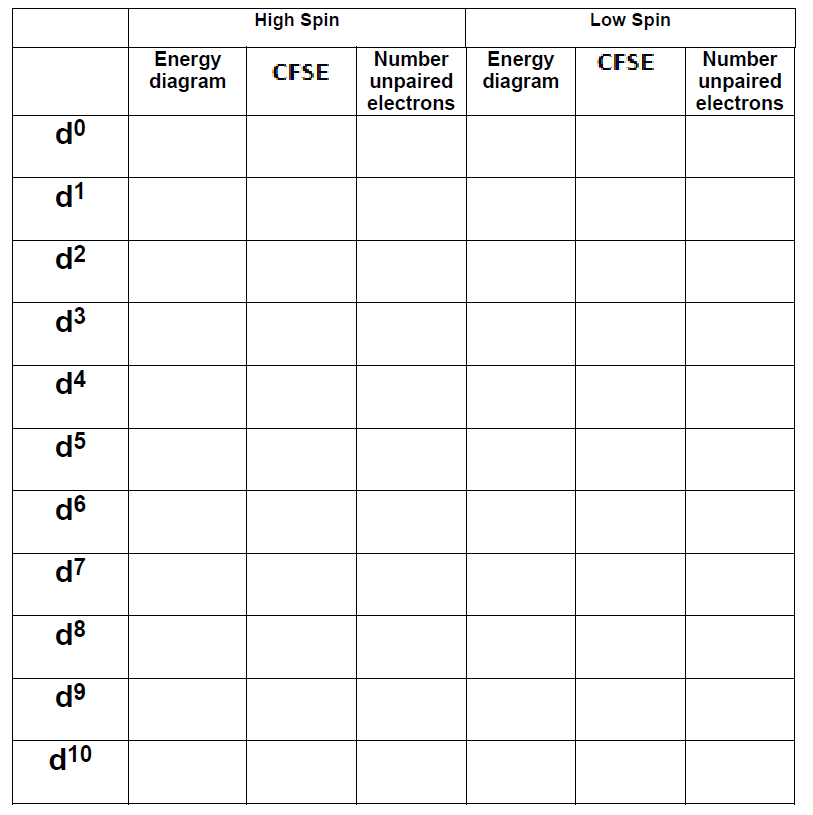
Complete the following table for octahedral metal ions in an octahedral crystal field. For each situation, sketch the energy splitting pattern, fill the orbitals, determine the total CSFE stabilization and the number of unpaired electrons. For electron configurations such as \(d^1\), where high/low spin is not an option, just show your work in the “high-spin” columns in the table and leave the low spin columns blank.
Q18: Factors affecting \(\Delta_o\)
- The binding ability of the ligand affects \(Δ_o\). Ligands that bind strongly increase the size of \(Δ_o\) and are called “strong field ligands.” Weak field ligands do not increase the size of Δo. All ligands can be listed in an order called the spectochemical series:
\[I^- < Br^- < SCN^- < Cl^- < F^- < OH^- < ox < H_2O < NCS^- < py , NH_3 < en < bpy < NO_2^- < CH_3^- < CN_- < CO \nonumber \]
Weak field ligands … Strong field ligands
High-spin complexes … Low-spin complexes
in which py = pyridine; en = ethylenediamine; bpy = 2,2'-bipyridine; SCN means the ligand is bound via sulfur and NCS via nitrogen (remember that these are linkage isomers). The list can vary from one metal ion to another, since some ligands bind preferentially to certain metals.
- The nature of the metal ion has an impact on whether the complex will be high- or low-spin. List two important factors that contribute to the metal's role.
Questions to master
E1
Which these compounds is paramagnetic (unpaired electrons present)?
- \(\ce{K_3[FeCl_6]}\)
- \(\ce{KMnO_4}\)
- \(\ce{ZnSO_4}\)
- \(\ce{TiCl_4}\)
E2
The number of unpaired electrons in \(K_4[Co(CN)_6]\) is
- 0
- 1
- 2
- 3
- None of these
E3
Which compound is diamagnetic (all electron paired)?
- \(\ce{K_4[Co(CN)_6]}\)
- \(\ce{[Cr(NH_3)_6]SO_4}\)
- \(\ce{[Mn(H2O)_6](Cl)_2}\)
- \(\ce{K_2[ZnCl_4]}\)
- \(\ce{K_3[FeCl_6]}\)
E4
Which would have the largest value of \(Δ_o\)?
- \(\ce{Fe(CN)_6^{-3}}\)
- \(\ce{Fe(CN)_6^{-4}}\)
- \(\ce{Co(NH_3)_6^{+2}}\)
- \(\ce{Ni(NH_3)_4^{+2}}\)
- \(\ce{Co(NH_3)_3(Cl)_3}\)
E5
Which would have the largest crystal field stabilization energy?
- octahedral complex with \(d^3\) configuration
- octahedral complex with \(d^4\) low spin configuration
- tetrahedral complex with \(d^5\) configuration
E6
Which complex ions in each pair is most likely to be high spin?
- \(\ce{Ru(H_2O)_6^{+3}}\) and \(\ce{Fe(H_2O)_6^{+3}}\)
- \(\ce{Mn(Cl)_6^{-3}}\) and \(\ce{Mn(Cl)_6^{-4}}\)
- \(\ce{Fe(Cl)_6^{-3}}\) and \(\ce{Fe(Cl)_4^{-}}\)
- \(\ce{Ni(NH_3)_4^{+2}}\) and \(\ce{Pt(NH_3)_4^{+2}}\)
- \(\ce{Fe(CN)_6^{-3}}\) and \(\ce{Fe(H_2O)_6^{+3}}\)
E7
Which is not a factor when predicting \(\Delta_o\)?
- oxidation state of metal
- Spectrochemical series
- whether the metal is from n = 3, 4 or 5.
- the geometry of the complex.
- the charge on the ligand

