Colligative Properties (Worksheet)
- Page ID
- 96803
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Template:HideTOCWork in groups on these problems. You should try to answer the questions without accessing the Internet.
Boiling point elevation and freezing point depression
When a non-volatile solute is dissolved in a volatile solvent, the boiling point increases and the freezing point decreases (as though the solute hinders the solvent getting into the vapor phase!)
Q6.1
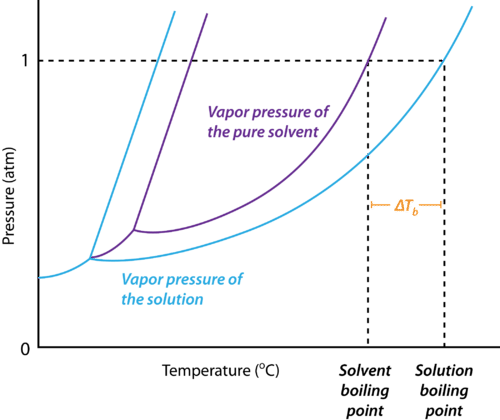
Recall that a liquid boils when its vapor pressure is equal to the surrounding pressure (If the liquid is in an open container, the surrounding pressure is the atmospheric pressure). Why does the boiling point go up when a solute is dissolved in water?
Q6.2
When pure water is heated, the temperature rises until it begins to boil and the temperature remains constant until all the water is evaporated. When a salt solution is heated, the temperature continues to rise even after it begins to boil. Why?
Q6.3
Freezing point / melting point is the temperature at which the liquid and solid phases are in equilibrium. We can use a phase diagram to help us see that a solution must have a lower freezing point than the pure solvent.
Q6.4
We can also understand freezing point depression by thinking about the rates of freezing and melting. Consider pure water in equilibrium with its own solid phase (ice). At this point, the rate of freezing is equal to the rate of melting and the temperature is 0oC. Now add a solute (like NaCl) to the liquid phase.
- Suddenly the rate at which the water freezes decreases. Why?
- What happens the rate of melting?
- If the temperature remains at 0oC, all of the ice melts, why? (This is why we put salt on icy roads!)
- What can you do to get ice to form again? Explain.
- When a solution freezes, the solid phase is composed of pure (or nearly pure) water. (See the figure below.) This provides another nice way to purify water from the ocean!) When you cool pure water, it begins to freeze when the temperature reaches 0oC and the temperature remains constant until all of the water is frozen. When you cool a solution, the temperature continues to drop even after the water begins to freeze. Why?
Calculations
The increase in the boiling point and the decrease in freezing point are directly proportional to the total molality of solute particles.
\[\Delta T_b = i\, K_b \,m \nonumber \]
\(\Delta T\) is positive because the boiling point increases.
\[\Delta T_f = − i\, K_f \,m \nonumber \]
\(\Delta T\) is negative because the freezing point decreases.
- \(m\) is the molality of the solute (molality = moles of solute per kilogram of solvent).
- \(K_b\) is the molal boiling-point-elevation constant
- \(K_f\) is the molal freezing-point-depression constant
- \(i\) is the van ’t Hoff factor which is the number of moles of particles that appear in solution for every mole of solute that dissolves (more on this below).
\(m \times i\) is total molality of solute particles (\(i\) = 1 for all solutes except ionic compounds) and \(K_b\) and \(K_f\) are different for each solvent. For water: \(K_b\) = 0.51 °C/m and \(K_f\) = 1.86 °C/m
Q6.5
Which of the following solutions has the lowest freezing point and the highest boiling point? (Simply find the solution with the highest value of \(m \times i\).)
- 0.100 m sucrose
- 0.050 m CaCl2
- 0.050 m NaCl
Q6.6
Calculate the freezing and boiling points for a 0.100 m aqueous solution of KCl.
Q6.7
Careful measurement shows that the solution in problem 6 actually freezes at -0.344oC. The solution behaves as though the concentration of solute particles is only 0.185 m instead of 0.200 m. Why?
Q6.8: Activities
The table below gives the experimental values of \(i\) for several solutions at various concentrations at 25°C:
| Solute | 0.100 m | 0.0100 m | 0.00100 m | Limiting value (infinite dilution) |
|---|---|---|---|---|
| Sucrose | 1.00 | 1.00 | 1.00 | 1.00 |
| NaCl | 1.87 | 1.94 | 1.97 | 2.00 |
| MgSO4 | 1.21 | 1.53 | 1.82 | 2.00 |
| K2SO4 | 2.32 | 2.70 | 2.84 | 3.00 |
- For ionic compounds, the van ’t Hoff factor depends on the concentration of the solute. As the concentration drops, \(i\) increases and eventually reaches the limiting (or ideal) value. Why?
- For both NaCl and MgSO4, the limiting value (ideal value) for \(i\) is 2. At a given concentration (except in very dilute solution) the experimental value for \(i\) is lower for MgSO4 than for NaCl. Why?
Note: For most problems, we will assume that we are dealing with ideal solutions. Thus, we will assume that solutions obey Raoult’s law and that the van ’t Hoff factor is the ideal value.
Osmotic Pressure
Q6.9
In an osmotic pressure demonstration, a semi-permeable membrane that contains sugar water is connected to a glass column and submerged into a beaker of pure water. The membrane allows water molecules to pass through but not solute molecules. Over time, the fluid rises up the column. This process is called osmosis. Why does the liquid rise up the column? (Think about the rate of water flow in both directions.) Eventually, the liquid stops rising. Why? (Something is opposing the flow of water). At the start of the demonstration, could we have prevented the liquid from rising at all? How?
Q6.10
The osmotic pressure of a solution is operationally defined as the pressure that must be exerted on the surface of the solution to prevent osmosis. What would happen if even more pressure were applied? (This is called reverse osmosis and is commonly used to purify sea water!)
Q6.11
Two solutions with the same osmotic pressure (same concentration of solutes) are said to be isotonic. Why must intravenous fluids be isotonic with your blood?
Osmotic pressure is a colligative property of a solution. That is, its magnitude depends on the concentration of dissolved particles but does not depend on the nature of the dissolved particles. Interestingly, osmotic pressure (\(\Pi\)) can be calculated using an equation that is very similar to the ideal gas equation:
\[\Pi V = nRT \nonumber \]
or
\[\Pi = MRT \nonumber \]
with
- \(M\) is the total molarity of solute particles (typically, problems will involve nonelectrolytes)
- \(R\) is the ideal gas constant (0.0821 L-atm/mol-K)
- \(T\) is the absolute temperature
Using colligative properties to calculate the molar mass of a nonvolatile, non-electrolyte. One of the most important applications of colligative properties is that they can be used to determine molar mass. This is done as follows:
- A known mass of a substance is dissolved in a known volume of solution or mass of solvent. (Since you know the mass of solute, you just need to figure out the number of moles to calculate a molar mass.)
- Either vapor pressure, boiling point elevation, freezing point depression, or (most commonly) osmotic pressure is measured and the appropriate equation is used to calculate the concentration (molarity from osmotic pressure, molality from boiling or freezing point, mole fraction from vapor pressure).
- The number of moles of the substance in the solution is determined from the calculated molarity and the known volume of solution (osmotic pressure) or the calculated molality and the known mass of solvent (boiling point or freezing point).
Q6.12
A sample of 2.05 g of the plastic polystryrene was dissolved in enough toluene to form 100 mL of solution. The osmotic pressure of this solution was found to be 1.21 kPa at 25oC. Calculate the molar mass of the polystyrene.

