6B: Kinetics - Concluded (Worksheet)
- Page ID
- 81626
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
The half-life idea is most useful in conjunction with first-order kinetics, which include many chemical reactions and all nuclear decay processes. The half life of a first-order process is a constant that indicates the amount of time it takes for an initial concentration to diminish to half as much material. From a consideration of the form of the integrated rate law, we can derive an expression that relates the half-life period to the first-order rate constant, k.
All chemical reactions have a faster rate at higher temperature. From this we can conclude that the magnitude of the rate constant, k, increases with rising temperature. This behavior is related to the energy barriers associated with the mechanism of the reaction, the set of molecular-level steps by which the reaction proceeds. Ultimately, the experimentally observed rate law is a consequence of the particular mechanism of the reaction and the energy barriers of the individual steps. Thus, if we propose a sequence of steps as a possible mechanism for a reaction, it should predict the rate law relationships of the experimentally determined rate law equation. Knowing the rate law, we can determine if a proposed mechanism is or is not reasonable for the reaction.
Learning Objectives
- Understand the concept of half life
- Understand the Arrhenius concept of the relationship between rate and temperature
- Know the various types of elementary steps that can compose a reaction mechanism
- Know how the molecularity of an elementary step relates to the rate expression for that step
- Understand the connection between the observed differential rate law of a reaction and its mechanism
Success Criteria
- Be able to carry out simple half-life calculations for first-order reactions
- Be able to sketch an Arrhenius reaction profile and calculate activation energies and reaction enthalpies
- Be able to carry out calculations with the Arrhenius equation
- Be able to determine whether or not a proposed simple mechanism is consistent with kinetic data
Half Life
For any reaction we can define the half-life (symbolized \(t_{1/2}\)) as that time required for the concentration of a reactant to diminish to half of what its value was at some initial time. Thus, at \(t = t_{1/2}\) we have \([A] = ½[A]_o\). The half-life period is a constant for a first-order reaction. (For second-order reactions, it depends on the initial concentration.) For first-order reactions, we can obtain an expression for the relationship between the \(t_{1/2}\) value and the value of the rate constant, \(k\), by substituting into the first-order integrated rate law expression. Recall that the integrated rate law expression for a first-order reaction is given by
\[ -\ln \left( \dfrac{[A]}{[A]_o} \right) = kt \label{1} \]
\[ \ln \left( \dfrac{[A]}{[A]_o} \right) = -kt \label{2} \]
\[ \ln \left( \dfrac{[A]_o}{[A]} \right) = kt \label{3} \]
Using Equation \(\ref{3}\), let us look at that point in the reaction when the initial concentration of \(A\), \([A]_o\), has diminished to half as much material, a value of \(½[A]_o\). This point will occur at a period of time that defines the half life for the reaction, \(t_{1/2}\). Substituting the values of initial concentration of \(A\) and concentration at the end of the half-life period into the integrated rate law expression, we can write
\[ \ln \left( \dfrac{[A]_o}{[A]} \right) = \ln \left( \dfrac{[A]_o}{½[A]_o} \right) = kt_{1/2} \nonumber \]
\[ \ln 2 = kt_{1/2} \approx 0.693 \nonumber \]
\[ t_{1/2} \approx \dfrac{0.693}{k} \nonumber \]
This shows that the half life, \(t_{1/2}\), is a characteristic constant of any first-order reaction, and that it is inversely proportional to the rate constant, \(k\), of the reaction. The half-life concept means that after each \(t_{1/2}\) period only half as much \(A\) will remain, compared to what was present at the beginning of the period. Let us define the number of half-life periods that have elapsed as \(h = t/t_{1/2}\), the total time divided by the length of one half-life period. What happens if we allow the reaction to continue to run through one, two, three, or more half-life time periods? For an initial concentration \([A]_o\), the table below shows the amount of \(A\), \([A]\), that will remain after each successive half-life period.
| elapsed time | 0 | \(t_{1/2}\) | \(2t_{1/2}\) | \(3t_{1/2}\) | ... |
|---|---|---|---|---|---|
| number of half-life periods, \(h\) | 0 | 1 | 2 | 3 | ... |
| amount of A remaining, \([A]\) | \([A]_o\) | \(\dfrac{1}{2} [A]_o\) | \(\dfrac{1}{4} [A]_o\) | \(\dfrac{1}{8} [A]_o\) |
Looking at the pattern of the decline in \([A]\) with number of elapse half-life periods, \(h\), we can see that it follows the relationship
\[[A]= \left(\dfrac{1}{2}\right)^h [A]_o \nonumber \]
This equation is valid even when \(h\) is not an integer. For example, suppose we allowed the reaction to run for one and a quarter half-life periods; i. e., \(h = 1.25\). Then, the amount of \(A\) remaining would be
\[\begin{align*} [A] &= \left(\dfrac{1}{2}\right)^{1.25} [A]_o \\[4pt] &= 0.421 [A]_o \end{align*} \]
Notice that the amount of \(A\) remaining in this case is less than \(0.50 [A]_o\) and more than \(0.25 [A]_0\), the amounts that remain after one and two half-life periods, respectively.
Q1
Consider the first-order decomposition reaction \(AB(s) \rightarrow A(s) + B(g)\), for which \(t_{1/2} = 10 \,s\) at 1000 K. If a 16.0-mol sample of AB(s) is allowed to decompose at 1000 K, how much material will remain after (a) 10 s, (b) 20 s, (c) 30 s, (d) 40 s?
Q2
A first-order reaction \(X_2 \rightarrow 2X\) initially has a reactant concentration of 4.80 mol/L. After running for 96 s, \(X_2\) concentration is 0.600 mol/L. What is the half-life period of the reaction? What is the value of the rate constant, k?
Q3
A first-order reaction \(A \rightarrow B\) initially has a reactant concentration of 12.0 mol/L. If the reaction has a half life of 36.0 seconds, how much reactant will remain after 54.0 seconds?
Rate and Temperature
Most chemical reactions speed up as temperature increases. For example, in a typical chemical reaction it is not unusual for the rate to double for every 10 °C increase in temperature. In terms of the differential rate law, this means that the rate constant, k, increases with temperature. The first successful interpretation of the relationship between \(k\) and \(T\) was made by Arrhenius in 1887 who reasoned that any reaction process must proceed through a transition state, involving formation of a high-energy species, called the activated complex, which then breaks apart to form products. Suppose we have the hypothetical reaction
\[A + B \rightarrow C + D \nonumber \]
which proceeds by a single-step mechanism in which \(A\) and \(B\) molecules come together to form products. We might imagine the reaction proceeding through the following process
\[A + B \rightarrow [AB^‡] \rightarrow C + D \nonumber \]
in which \([AB^‡]\) is the transition state species (also called the activated complex) which decomposes to give the products \(C\) and \(D\).
This can be illustrated with an Arrhenius plot, which is a semi-quantitative representation of the energy of the system in the process of converting from reactants to products. For this exothermic, one-step reaction, the Arrhenius plot might look like Figure \(\PageIndex{1}\) (left) and for an endothermic one-step reaction, the Arrhenius plot might look like Figure \(\PageIndex{1}\) (right).
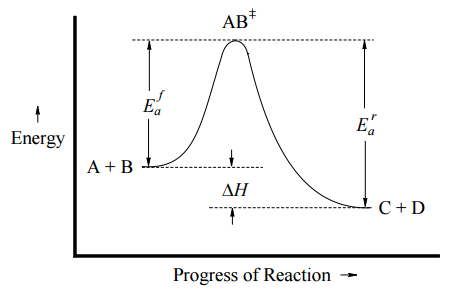
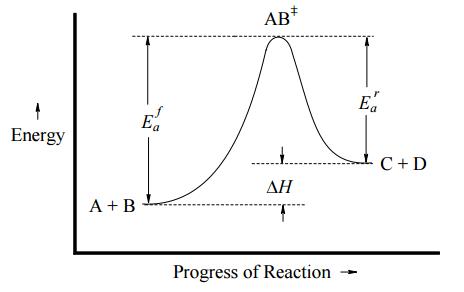
In both cases, \(E_a^f\) is the activation energy of the forward reaction, and \(E_a^r\) is the activation energy for the reverse reaction. In either direction, the activation energy represents an energy barrier that must be overcome for reaction to occur. Note:
- If \(E_a^f < E_a^r\), then \(ΔH_{rxn} < 0\) (exothermic)
- If \(E_a^f > E_a^r\), then \(ΔH_{rxn} > 0\) (endothermic)
Q4
The reaction, \[\ce{2 NOCl(g) -> 2 NO(g) + Cl2(g)} \nonumber \]
is believed to proceed by a one-step mechanism. Its standard enthalpy is \(ΔH^o = +75.5\, kJ/mol\). The activation energy of the forward reaction is 98.2 kJ/mol. Sketch the Arrhenius plot for the reaction. What is the value of \(E_a^r\) for the activation energy of the reverse reaction?
Arrhenius Equation
Arrhenius was able to take this model and develop an equation for the relationship between a reaction’s rate constant, k, and the absolute temperature, T. The Arrhenius equation is
\[ k =A e^{-E_a/RT} \nonumber \]
where \(A\) is a constant (called the Arrhenius constant) and \(E_a\) is the activation energy. The value of \(A\) for a reaction is determined by the characteristics of the reactants, including possible orientation requirements for effective reaction.
If we take logarithms of both sides of the Arrhenius equation we obtain
\[\ln k = \ln A - E_a /RT \label{A0} \]
Rearranging Equation \(\ref{A0}\),
\[\ln k = \dfrac{-E_a}{R} \left( \dfrac{1}{T} \right) + \ln A \nonumber \]
This is a straight line equation, in which \(\ln k\) is the \(y\) variable, \(1/T\) is the \(x\) variable, and \(\ln A\) is \(y\)-intercept.
Because only two points are needed to define a straight line, only two pairs of \(\ln k\) and \(1/T\) data are needed to define the slope. This being the case, we can obtain a single equation that relates the two pairs of \(\ln k\) and \(1/T\) data to the value of \(E_a\). At any two temperatures, \(T_1\) and \(T_2\), we can write
\[\ln k_1 = \dfrac{-E_a}{R} \left( \dfrac{1}{T_1} \right) + \ln A \label{A1} \]
\[\ln k_2 = \dfrac{-E_a}{R} \left( \dfrac{1}{T_2} \right) + \ln A \label{A2} \]
Subtracting the Equation \(\ref{A2}\) from Equation \(\ref{A1}\), we obtain
\[\ln k_1 -\ln k_2 = \dfrac{-E_a}{R} \left( \dfrac{1}{T_1} \right) \cancel{+ \ln A} - \dfrac{-E_a}{R} \left( \dfrac{1}{T_2} \right) \cancel{- \ln A} \nonumber \]
\[\ln \dfrac{k_1}{k_2} = \dfrac{E_a}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_1} \right) \label{A3} \]
Equation \(\ref{A3}\) allows us to calculate \(E_a\) from kinetic data that give the rate constant for the reaction at two temperatures. Moreover, proceeding in this manner we do not need to know \(A\), the Arrhenius constant (although we can calculate that by then using knowledge of \(E_a\) and Equation \(\ref{A0}\).
Q5
Sketch a plot of ln k vs. 1/T. What is the value of the slope? What information can be obtained from the y intercept?
Q6
For the reaction
\[2 NOCl(g) \rightarrow 2 NO(g) + Cl_2(g) \nonumber \]
the experimentally determined rate law is
\[Rate = \dfrac{d[Cl_2]}{dt} = k[NOCl]^2 \nonumber \]
The rate constant, k, is \(2.6 \times 10^{–8} L/mol \cdot s\) at 300 K and \(4.9 \times 10^{-4} L/mol \cdot s\) at 400 K. What is the activation energy, \(E_a\), of the reaction?
Mechanisms, Elementary Reactions, and Rate Law
The mechanism of a reaction is composed of a series of molecular-level steps, called elementary reactions or elementary steps. In representing the mechanism, these elementary reactions are written in the same way that we write overall reaction equations. However, in this context, they are given a special meaning: they are representations of what is presumed to occur on the molecular level. Unlike reaction equations in general, we can make a direct connection between the stoichiometry of the elementary reaction and the order with respect to each species in differential rate law expression for that step.
On the molecular level, we can conceive of three plausible kinds of elementary reactions, depending on whether one, two, or three molecules are involved. Hence, every elementary reaction in a mechanism can be categorized as either unimolecular, bimolecular, or termolecular. These terms refer to the molecularity of the elementary reaction.
We can relate the molecularity of an elementary reaction to the rate law expression for that step by applying the Law of Mass Action:
For any elementary reaction, the rate law expression for that step is proportional to the concentration of each reactant such that the molecularity determines the overall order.
Suppose we consider the elementary process of chlorine molecules, \(Cl_2\), dissociating to form chlorine atoms (free radicals), \(Cl^•\):
\[Cl_2 \rightarrow 2Cl^• \nonumber \]
The more \(Cl_2\) we have, the more \(Cl^•\) will form, or in other words the rate is directly proportional to the concentration of \(Cl_2\) and nothing else. Thus, for this elementary reaction, occurring at the molecular level, we can write its rate as
\[rate = k[Cl_2] \nonumber \]
Note that this unimolecular process has a first-order rate law. [We will use rate (not capitalized) to refer to the rate of an elementary reaction, and Rate (capitalized) to refer to the rate of an overall reaction; the two are not generally the same.]
By a similar reasoning, we can conclude that a bimolecular elementary process should have a rate law that is second-order overall, first order in each of the two participating species. For example, if the elementary process is \(A + B \rightarrow products\), then the rate law for this step would be \(rate = k[A][B]\). Likewise, a termolecular elementary step should have a rate law that is third-order overall, first order in each of the participating species. For example, if the elementary process is \(A + B + C \rightarrow products\), then the rate law for this step would be
\[rate = k[A][B][C]. \nonumber \]
Q7
Answer the following questions about elementary step molecularity and the rate expression for the step:
- Consider the elementary reaction \(2 NO_2 \rightarrow N_2O_4\). What is the molecularity of this step? What is the rate law expression for this step?
- Consider the elementary reaction \(Cl^• + H_2 \rightarrow HCl + H^•\). What is the molecularity of this step? What is the rate law expression for this step?
- Consider the elementary reaction \(H^+ + Br^– + H_2O_2 \rightarrow HOBr + H_2O\). What is the molecularity of this step? What is the rate law expression for this step?
- The highest conceivable molecularity is termolecular. Why?
Proposing Mechanisms and the Rate Determining Step Concept
The mechanism of a reaction, consisting of one or more elementary steps, must add up to give the overall stoichiometry of the reaction. Moreover, the sequence of steps and the individual rates of each elementary process must result in a predicted overall rate law expression that has the same form as the overall rate law for the reaction determined by experiment. Thus, the initial piece of information the chemist uses is the observed rate law, with its various orders with respect to reacting species. Then, using knowledge about the reactivity of the various species, the chemist proposes a series of steps that will add to give the overall stoichiometry and that can be shown to yield a rate law with the same orders as the observed rate law. Except in very carefully chosen cases, this process is beyond reasonable expectations for a beginning chemistry student (i.e., you’re not going to be asked to propose mechanisms on a test!) However, it is important to be able to understand how a proposed mechanism is consistent (or not) with the observed rate law.
In many cases, one step in the proposed mechanism may be significantly slower than others. Such a step is called a rate determining step, because the overall reaction rate can be no faster than the rate at that step. If a rate determining step occurs, the overall rate expression must be equivalent to the rate expression at that step. In terms of the Arrhenius concept, the rate determining step has the highest activation energy, \(E_a\), of all the steps in the mechanism, and therefore it has the smallest rate constant, k. For example, consider the hypothetical reaction \(A \rightarrow D\), proceeding by a three-step mechanism in which the second step is significantly slower than the others and therefore rate determining.
| Elementary Step | Speed of Step | rate law | |
|---|---|---|---|
| \( A \rightarrow B\) | fast | \(rate_1 = k_1[A]\) | |
| \( B \rightarrow C\) | slow | \(rate_2 = k_2[B]\) | rate determining step |
| \(C \rightarrow D\) | fast | \(rate_3 = k_3[C]\) |
The overall reaction is
\[A \rightarrow D \nonumber \]
with the following observed rate
\[Rate = rate_2 \nonumber \]
The reaction profile for this hypothetical mechanism is shown below.
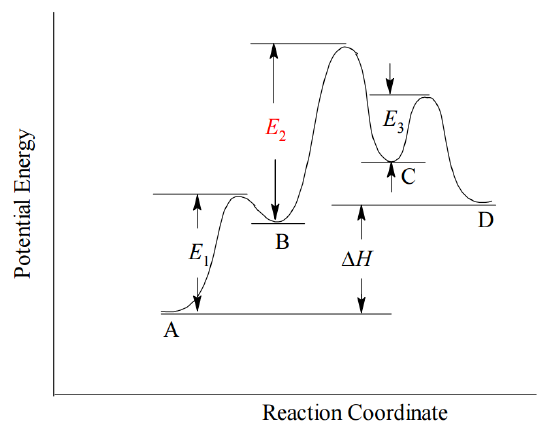
Because the second step is the slowest, the overall rate of the reaction is equivalent to the rate at step 2.
From the Law of Mass Action, we can always write down the rate expression for each mechanism step, including the rate-determining step, from its molecularity. However, unless the rate determining step is the first in the mechanism, its rate expression may depend upon concentrations of species that are not initially present in the reaction mixture. Instead, the rate expression for the rate-determining step may involve species that are created temporarily in a prior step and then destroyed in the course of the mechanism. Such transient species are called reaction intermediates. In the example above, both \(B\) and \(C\) are reaction intermediates, because they are produced in one step and consumed in a subsequent step. The dependence of the rate determining step on the concentration of a reaction intermediate (here, \(B\)) means that the rate expression for the rate-determining step will not have the same form as the experimentally observed rate expression, which is always cast in terms of reactants present at the start of the reaction. In order to show that the proposed mechanism is consistent with the experimental data, it is often necessary to derive from the rate-determining step's rate expression an equivalent expression in terms of observable reactants (and sometimes products). The final proof of a proposed reaction mechanism is that it predicts the rate law expression observed by experiment, which is always cast in terms of observable reactants, not unobservable intermediates.
Q8
Refer to the plot shown above for the three-step mechanism by which the hypothetical reaction \(A \rightarrow D\) proceeds.
- From the plot, is the overall reaction exothermic or endothermic?
- If a reaction is exothermic or endothermic, must all its steps be the same (exothermic or endothermic)?
- Step 2 in the hypothetical mechanism is rate determining. Why must it have the highest activation energy?
- Look at the proposed mechanism. Why would a slow rate at step 2 slow down the whole reaction? In other words, what does it do that makes its rate the rate-determining step?
Q9
Consider the following chemical reaction in aqueous solution,
\[2I^– + 2H^+ + H_2O_2 \rightarrow I_2 + 2H_2O \nonumber \]
for which the experimentally determined rate law expression is
\[\text{Rate} = k[I^–][H_2O_2] \nonumber \]
The following mechanism has been proposed:
| Elementary Step | Speed of Step | rate law | |
|---|---|---|---|
| \( I^– + H_2O_2 \rightarrow HOI + OH^–\) | slow | \(rate_1 = k_1[A]\) | |
| \( HOI + I^– \rightarrow OH^– + I_2\) | fast | \(rate_2 = k_2[B]\) | |
| \(H^+ + OH^– \rightarrow H_2O\) | fast | \(rate_3 = k_3[C]\) |
- Show that this series of steps gives the overall stoichiometry of the reaction. [Note: sometimes it is necessary to multiply one or more steps by appropriate factors to make everything add up to the overall stoichiometry. These factors are usually omitted when writing the series of mechanism steps, as this case illustrates.]
- From the molecularity, write the rate law expression for each step.
- Identify the reaction intermediates in this mechanism.
- Explain how this mechanism is consistent with the experimentally observed rate law.
Q10
Consider the gas phase reaction
\[2 N_2O_5 \rightarrow 4 NO_2 + O_2 \nonumber \]
for which the observed rate law expression is
\[Rate = k[N_2O_5] \nonumber \]
The following mechanism has been proposed:
| Elementary Step | Speed of Step | rate constant | |
|---|---|---|---|
| \( N_2O_5 \rightleftharpoons NO_2 + NO_3\) | fast equilibrium | \(k_1 (forward)\) & \(k_{-1} (reverse)\) | |
| \( NO_2 + NO_3 \rightarrow NO + NO_2 + O_2\) | slow | \(k_2\) | |
| \(NO_3 + NO \rightarrow 2NO_2\) | fast | \(k_3\) |
Carry out the following steps to show that this is a plausible mechanism.
- Show that this series of steps adds to give the overall stoichiometry of the reaction. [Hint: One step needs to be multiplied by an integer factor.]
- Write the rate law for each step. The first step (fast equilibrium) is reversible, so you will need to write two rate law expressions, one for each direction.
- Which step is rate determining? Write its rate law expression.
- What species are reaction intermediates?
- Your rate expression, based on the rate expression for the rate-determining step, contains a concentration term for an unobservable reaction intermediate. We need to express the rate law for the rate determining step in terms of observable starting materials. Note that the first step is a rapidly established equilibrium, which means its rate in the forward direction is exactly the same as in the reverse direction. Write an equality between your two expressions for the two directions, and rearrange it to solve for \([NO_3]\).
- Substitute your expression for \([NO_3]\) into your expression for the rate law of the rate determining step. Does this agree with the experimentally observed rate law expression?


