6A: Oxidation Numbers, Redox Reactions, Solution Concentration, and Titrations (Worksheet)
- Page ID
- 81595
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
In addition to metathetical reactions, electron transfer reactions often occur in solutions. When electrons are transferred from one chemical species to another oxidation and reduction are said to have occurred. These kinds of reactions are very important in natural and synthetic processes. One way of tracking these changes is to look at assigned oxidation numbers on each element in the chemical species involved in the reaction.
To round out our discussions of solution reactions, we need to address the quantitative relationships between reactants and products. Up to now, we have used the connection between mass and moles to do this. When dealing with solutions, it is usually more convenient to analyze the stoichiometry in terms of mole-based solution concentration terms. An important application of this is the analytical technique of titration, used to determine the amount of a substance, such as an acid or base, in a solution. It is based on the quantitative relationships between volume and the mole-based solution concentration molarity.
Learning Objectives
- Understand the rules for assigning oxidation numbers
- Understand the concepts of oxidation and reduction in terms of oxidation numbers
- Understand solution concentration in terms of molarity
- Know the connection between molarity, volume, and moles or millimoles of solute
- Understand the difference between analytical concentration and actual species concentration
- Understand the techniques of titration and the quantitative relationships on which it is based
Success Criteria
- Be able to assign oxidation numbers to elements in chemical species
- Be able to identify when a species is being oxidized or reduced
- Be able to calculate molarity of a solution
- Be able to convert between molarity, volume, and moles or millimoles
- Be able to assess the actual ion concentrations in a strong electrolyte solution
- Be able to carry out stoichiometry calculations using molarities and volumes of solutions
- Be able to carry out titration calculations
Redox and Oxidation Numbers
A reaction in which one species transfers electrons to another is called an oxidation-reduction reaction, also called a redox reaction. For example, consider the reaction of metallic iron with chlorine gas to form ionic iron(III) chloride:
\[2 Fe(s) + 3 Cl_2(g) \rightarrow 2 FeCl_3(s) º 2 [Fe^{3+}][Cl^–]_3 \nonumber \]
We can think of this as the net transfer of six electrons from two iron atoms to three chlorine molecules:
\[ \underbrace{2 \times \, (Fe^0 \rightarrow Fe^{3+} + 3e^–)}_{\text{electrons "pushed" → oxidation}} \nonumber \]
\[ \underbrace{3 \times \, (Cl_2^0 + 2e^– \rightarrow 2Cl^–)}_{\text{electrons "pulled" → reduction}} \nonumber \]
In essence, the Fe "pushes" electrons and the Cl2 "pulls" electrons, thereby effecting electron transfer. On this basis, we have the following definitions:
- Oxidation - loss of electrons by a substance
- Reduction - gain of electrons by a substance
Oxidation and reduction always involve transfer of electrons. Therefore, there is never oxidation without reduction and vice versa in a redox reaction. Oxidizing something must cause something else to be reduced and vice versa. Therefore, the substance oxidized is seen to be the agent of the other substance's reduction, and the substance reduced is seen to be the agent of the other substance's oxidation. This leads to the following definitions:
Oxidizing agent (oxidant) a substance that causes another substance to be oxidized and is itself reduced.
Reducing agent (reductant) a substance that causes another substance to be reduced and is itself oxidized.
The transfer of electrons from one species to another changes the electron count and distribution about the atoms in both. One way of reflecting this is through changes in assigned oxidation numbers. Oxidation numbers are real or hypothetical charges on atoms, assigned by the following rules:
- Atoms in elements are assigned 0.
- All simple monatomic ions have oxidation numbers equal to their charges. (e.g., all Group 1 ions are +1; all group 2 ions are +2; all the following ions have oxidation numbers given by their charges - Fe2+, Al3+, S2-, N3-)
Fluorine is always -1 in its compounds.
- Halogens are usually -1, except when a central atom or when combined with a more electronegative element (e.g., assign I as -1 in NI3, but +3 in ICl3).
- Oxygen is -2 in most of its compounds, except in peroxides (H2O2, Na2O2) where it is -1.
- Hydrogen is usually +1, except in hydrides with electropositive elements, particularly with metal cations, where it is -1 (e.g., NaH, CaH2, BH4–).
- The sum of all oxidation numbers for a neutral compound is zero; the sum is the charge on the species for a complex ion.
When a species is oxidized, one of its atoms goes to a higher (more positive or less negative) oxidation number. When a species is reduced, one of its atoms goes to a lower (less positive or more negative) oxidation number. For example, in the reaction between metallic iron and gaseous chlorine, the oxidation state of Fe goes from 0 to +3, making this an oxidation, and the oxidation number of each Cl goes from 0 to –1, making this a reduction.
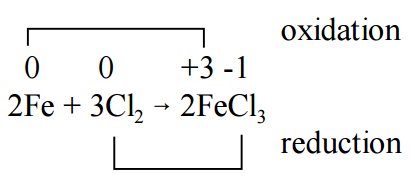
We will discuss electronegativity in more detail later. For now, electronegativity can be defined as the ability of an atom in a compound to attract electrons to itself. In the periodic table, electronegativity increases left to right and bottom to top; e.g., O < F, I < Cl, Cl < O. Overall, the most electronegative elements are in the upper right, and the least electronegative elements are in the lower left of the periodic table.
Q1
Assign the oxidation numbers of each element in the following chemical species: HCl, H2O, NH3, NO3–, K2Cr2O7, Hg2Cl2, HgCl2, Al(OH)3, Na3PO4
Q2
Which element is oxidized and which element is reduced in the following redox reactions?
- \(Zn(s) + 2 HCl(aq) \rightarrow ZnCl_2(aq) + H_2(g)\)
- \(Fe_2O_3(s) + 2 Al(s) \rightarrow 2 Fe(s) + Al_2O_3(s)\)
- \(14 HNO_3 + 3 Cu_2O \rightarrow 6 Cu(NO_3)_2 + 2 NO + 7 H_2O\)
- \(I^– + 2 MnO_4^– + H_2O \rightarrow IO_3^– + 2 MnO_2 + 2 OH^–\)
Solution Concentration
Solution concentration is a statement of the amount of solute present in a solution relative to either the amount of solvent or the amount of solution. The most frequently used expression of concentration in chemistry is molarity (symbol M). Molarity is defined numerically by:
\[ \text{Molarity} = M = \dfrac{\text{moles of solute}}{\text{liters of solution}} \nonumber \]
Sometimes it is more convenient to think of molarity in terms of millimoles of solute (10–3 mole) and milliliters of solution (10–3 L). These units are both 0.001 of the units used to define molarity as shown above, so the ratio of millimoles of solute to milliliters of solution will be numerically the same. Therefore, when convenient, we can define the molarity of a given solution alternatively as
\[ \text{Molarity} = M = \dfrac{\text{millimoles of solute}}{\text{milliliters of solution}} \nonumber \]
By either definition, the numerical value of the molarity of a particular solution is the same. Solutions of a certain molarity are most often prepared by using a volumetric flask. If the solute can be obtained in high purity ("analytical reagent grade"), the needed amount can be weighed on an analytical balance and then quantitatively transferred (no loss) to the volumetric flask. Solvent, usually water, is then added until the level reaches the calibration mark for the flask's volume. The stoppered flask must be shaken thoroughly to ensure proper mixing.
The advantage of knowing solution concentration in molarity is the direct relationship between the volume of a sample of the solution and the number of moles of solute it contains. If we take the product of a solution's molarity times its volume in liters, we can see by dimensional analysis that the resulting units will be moles of solute:
\[ M V_l= \left( \dfrac{\text{mol solute}}{ \cancel{\text{L solution}}} \right) ( \cancel{\text{L solution}}) = \text{mol solute} \nonumber \]
Similarly, the product of a solution's molarity times its volume in milliliters gives the number of millimoles (abbreviated mmol) in the sample:
\[ M V_{ml}= \left( \dfrac{\text{mol solute}}{ \cancel{\text{mL solution}}} \right) ( \cancel{\text{mL solution}}) = \text{mol solute} \nonumber \]
These two relationships are used routinely when dealing with solution concentrations in molarity. Another way of preparing a solution of a certain molarity is to start with a measured volume (an aliquot) of a more concentrated solution of known molarity and dilute to the desired concentration. The number of moles of solute in the aliquot of the concentrated solution can be calculated from M × V. Regardless of the dilution, this will be the number of moles in the new solution. Therefore, we can write
\[ \dfrac{M_{initial}}{V_{initial}} = M_{final}V_{final} \nonumber \]
or more simply
\[M_iV_i = M_fV_f \nonumber \]
Q3
Describe how you would go about making exactly 500 mL of 0.100 M NaNO3 (aq) solution, using reagent grade NaNO3 (s) (f.w. = 85.0 u).
Q4
Starting with a 0.100 M NaNO3 solution, how would you go about preparing exactly 100 mL of 0.0250 M NaNO3 solution?
Q5
How many milliliters of 0.0250 M CuSO4 solution contain 1.75 g of solute? (f.w. CuSO4 = 159.6 u)
Analytical Concentration vs. Actual Species Concentration
No molecular dissociation occurs when a nonelectrolyte is dissolved in water. In a nonelectrolyte solution, the molarity reflects the actual concentrations of solute molecules. Thus a 0.10 M sugar solution contains 0.10 mole of sugar molecules per liter of solution. The situation is different with electrolytes, because they break up to some extent to give ions in solution. The concentrations of those ions in solution depends upon
- the amount of electrolyte that is dissolved,
- whether the solute is a strong or weak electrolyte, and
- the formula of the electrolyte.
To talk about the concentrations of ions in weak electrolyte solutions, we will need to have some way of assessing the extent of dissociation of the solute. We will delay that topic until later. For now we will only consider predicting the concentrations of ions in solutions of strong electrolytes. Many chemists call the number of moles of solute dissolved per liter of solution the analytical concentration of solute, given the symbol \(C\). This is essentially a statement of the moles of solute per liter of solution that we dissolved, without regard to the concentrations of the species that are actually present in the solution (only ions, a mixture of molecules and ions, or only molecules). For solutions of strong electrolytes, the concentrations of ions can be taken as whole number multiples of the analytical concentration. We will indicate the actual concentration of a species X by writing its symbol in square brackets, \([X]\), meaning moles per liter of solution. For example, suppose we make a \(0.10\, M\, NaCl\) aquous solution; i.e., \(C = 0.10\, M\). All of the \(NaCl(s)\) breaks up to dissolve as \(Na^+ (aq)\) and \(Cl^– (aq)\) ions:
| \(NaCl(s)\) | \(\rightarrow\) | \(Na^+ (aq)\) | \(Cl^– (aq)\) | |
|---|---|---|---|---|
| Add | 0.10 M | 0 M | 0 M | |
| Result | 0 M | 0.10 M | 0.10 M |
From this we can say, \([Na^+ ] = 0.10\, M\), \([Cl^– ] = 0.10 \,M\), and the concentration of all ions (both cations and anions) is 0.20 M. Consider the same analytical concentration of \(Na_3PO_4\).
| \(Na_3PO_4\) | \(\rightarrow\) | \(3Na^+ (aq)\) | \(PO_4^{3–} (aq)\) | |
|---|---|---|---|---|
| Add | 0.10 M | 0 M | 0 M | |
| Result | 0 M | 0.30 M | 0.10 M |
From, this we can say, \([Na^+ ] = 0.30\, M\), \([PO_4^{3–}] = 0.10\, M\), and the concentration of all ions (both cations and anions) is \(0.40\, M\). Notice that this means that the 0.10 M solution of \(Na_3PO_4\) has twice the concentration of ions (0.40 M) as the 0.10 M solution of NaCl (0.20 M).
Q6
Which of the following has the highest concentration of sodium ion: \(0.20\, M\, NaCl\), \(0.13\, M \,Na_2SO_4\), \(0.080\, M\, Na_3PO_4\)?
Q7
Indicate the concentrations of all ions in a solution prepared by mixing 45.0 mL of \(0.200\, M\, Na_2SO_4\) and 65.0 mL of \(0.300\, M Al_2(SO_4)_3\).
Q8
How many grams of \(PbCl_2\) (f.w. = 278.1 u) are produced by the reaction
\[Pb(NO_3 )_2 (aq) + 2 NaCl(aq) \rightarrow PbCl_2 (s) + 2 NaNO_3 (aq) \nonumber \]
when 25.00 mL of \(0.4567\, M\, Pb(NO_3)_2\) solution and 25.00 mL of \(0.9876 \,M \,NaCl(aq)\) solution are mixed?
Titration
An important application of the relationships \(MV_L = mol\) and \(MV_{mL} = mmol\) is volumetric analysis, which uses precise measurement of the volume of a solution of known concentration, called a standard solution, as a means of carrying out chemical analysis. In titration, the most commonly used type of volumetric analysis, a standard solution (the titrant) with known concentration is added to a measured volume of a solution to be analyzed (the analyte) having unknown concentration. The titrant and analyte react with one another according to a known stoichiometry. By measuring the volume of titrant that completely consumes the analyte, it is possible to calculate the amount of analyte originally present in the sample solution (and therefore its concentration), using the known stoichiometric relationship between the two reactants. Titrant in buret standard solution = known concentration Analyte in reaction flask known volume, unknown concentration

In most cases, the stoichiometric relationship between the analyte and titrant is 1:1, or less frequently 1:2 or 1:3. The volume of the analyte is usually measured and dispensed into a reaction flask with a pipet. The titrant is added to this sample from a buret, which measures the amount of titrant delivered. The volume at which the stoichiometrically correct amount of titrant has been delivered to completely consume the analyte is called the equivalence point. Some means must be used to detect the equivalence point. One common method is to add a small amount of an indicator solution to the reaction flask. The indicator is chosen so that it will undergo a pronounced color change very near the equivalence point. The volume of titrant needed to cause the indicator to change color is called the end point of the titration. Ideally the end point and the equivalence point should be the same, but in most real situations there is a small difference between the two, which introduces a small error into the measurement. This error will be negligible if the indicator has been correctly chosen for the system being analyzed
Titration is often used to determine the concentration of a solution of an acid or base, employing the stoichiometry of a neutralization reaction. If the analyte is a weak or strong base, the titrant will be a standard solution of a strong acid, such as hydrochloric acid, HCl(aq). If the analyte is a weak or strong acid, the titrant will be a standard solution of a strong base, such as sodium hydroxide, NaOH(aq). The number of millimoles of titrant added to the analyte to reach the equivalence point is given by the product of the concentration of the standard solution in molarity times the volume delivered from the buret in milliliters:
\[\text{millimol titrant} = M_t \times V \nonumber \]
At the equivalence point, the stoichiometric relationship between the millimoles of titrant added and the millimoles of analyte initially present, based on the balanced neutralization equation, can be used to find the solution concentration of the sample. For example, if the analyte is a monoprotic acid and the titrant is a standard solution of NaOH(aq), the millimoles of acid initially present will be equal to the millimoles of NaOH(aq) added to reach the equivalence point, because the stoichiometry between moles of analyte and moles of titrant is 1:1. For example, in the titration of a sample of HCl(aq) with NaOH(aq) titrant, the titration equation is
\[NaOH(aq) + HCl(aq) \rightarrow NaCl(aq) + H_2O(l) \nonumber \]
and at the equivalence point we would have
\[mmol\, NaOH = mmol \,HCl \nonumber \]
\[M_{NaOH} V_{NaOH} = M_{HCl} V_{HCl} \nonumber \]
If the analyte is polyprotic (n = 2, 3, ...), \(n\) millimoles of titrant will be required for every millimole of analyte to reach the equivalence point:
\[mmol \,titrant = n \times mmol\, analyte \nonumber \]
\[M_tV_t = nM_aV_a \nonumber \]
For example, in the titration of a sample of \(H_2SO_4 (aq)\) with \(NaOH(aq)\), the titration equation is
\[2 NaOH(aq) + H_2SO_4 (aq) \rightarrow Na_2SO_4 (aq) + 2 H_2O(l) \nonumber \]
and at the equivalence point for consuming all the \(H_2SO_4\) we would have
\[M_{NaOH} V_{NaOH} = 2 \times M_{H_2SO_4 } V_{H_2SO_4 } \nonumber \]
Q9
Define the following terms: analyte, titrant, equivalence point, end point.
Q10
The following represent skeletal reaction equations for some possible titrations. For each, assume that the first species is the analyte and the second species is the titrant. Balance each equation. For each millimole of analyte, how many millimoles of titrant are needed for complete reaction in each case?
- \(HC_2H_3O_2 (aq) + NaOH(aq) \rightarrow H_2O(l) + NaC_2H_3O_2 (aq)\)
- \(Ca(OH)_2 (aq) + HCl(aq) \rightarrow H_2O(l) + CaCl_2 (aq) \)
- \(H_3PO_4 (aq) + KOH(aq) \rightarrow H_2O(l) + K_3PO_4 (aq)\)
Q11
A 25.00-mL sample of an unknown monoprotic acid is titrated to an equivalence point with 32.42 mL of 0.1000 M NaOH solution. What was the original concentration of acid in the sample?
Q12
How many milliliters of 0.1200 M \(\ce{HCl}\) solution are needed to completely neutralize 50.00 mL of 0.1012 M \(\ce{Ba(OH)2}\) solution?
Q13
A 20.00-mL sample of a chloride-containing solution was titrated with \(0.4000 \,M \,AgNO_3\) solution, requiring 28.62 mL to reach the equivalence point. Write the balanced reaction equation for this titration. What was the concentration of \(Cl^–\) ion in the original sample? How many grams of precipitate were formed?


