Size Exclusion Chromatography (Crawford, Kloepper)
- Page ID
- 287138
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
The goal of this activity is to introduce you to size exclusion chromatography, a technique that separates compounds on the basis of size.
Read and discuss the following with your group.
Introduction
The figure below shows a resin bead with one pore in it. It also shows representations for several molecules of different size.
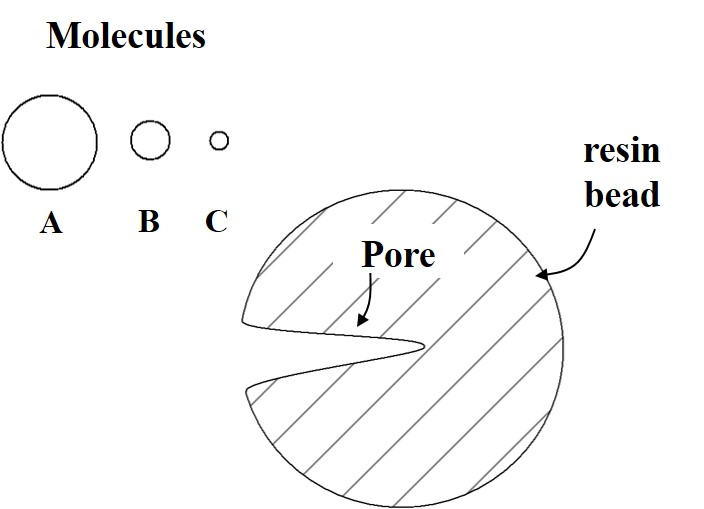
Note: this is not to scale! The pore size and molecule sizes shown are not representative of the scale that would exist in reality. The pore is bigger than would actually occur and the molecules would never have sizes that big relative to the size of the bead.
- Consider each molecule. How will each interact with the pore?
- Now consider a column filled with many of these beads. If a mixture of molecules A, B, and C are loaded, which will elute first? Last? Explain your reasoning.
In Figure 1, the resin bead was shown with one pore. In reality, the beads contain pores with tunnels (often an entrance and exit). The size of the pore can be controlled to some degree during the synthesis of the bead. Different pore sizes allow for the separation of differently-sized molecules (Figure 2).

- Consider Figure 3. For each molecule (X, Y, and Z) draw three possible paths they could take through the column.

Figure 3. Paths for X, Y, and Z.
- Predict the effect of increasing column length on resolution. Explain your answer using your work from questions 3 and 4.
- Now assume you have a mixture of X, Y, Z with a sufficient amount of resin. Based on your answers above, now draw a chromatogram showing the elution order of the three molecules and label the peaks. Justify your retention order.
- Suppose we had a molecule that was even larger than the biggest one in the picture above. Where would this elute in your chromatogram?
- Suppose we had a molecule that is smaller than the smallest pictured above. Where would this elute on your chromatogram?
- What is the stationary phase in size exclusion chromatography? The mobile phase?
- Describe the interaction(s) between the compounds X, Y, and Z and the stationary phase. Now do the same for the mobile phase.
- How do you know the size of a molecule?
Biochemical Connections
- Consider Table 1, which shows example resins for size exclusion columns. In some biochemical applications, these size exclusion columns are called desalting columns. Why do you think that is the case?
Table 1. Sephadex resins.
|
sephadex resin |
range (Da) |
|---|---|
|
G10 |
100 – 800 |
|
G15 |
500 – 1500 |
|
G25 |
1000 – 5000 |
|
G50 |
1500 – 30,000 |
|
G75 |
3000 – 80,000 |
|
G100 |
4000 – 150,000 |
|
G150 |
5000 – 300,000 |
|
G200 |
5000 – 600, 000 |
- Consider Table 2. Which property would be most of interest for size exclusion chromatography?
Table 2. Protein information
|
protein |
Da |
pI |
interacts with |
|---|---|---|---|
|
D |
13,000 |
4.3 |
O2 |
|
E |
54,000 |
9.5 |
ATP |
|
F |
150,000 |
6.7 |
--- |
|
G |
56,000 |
4.5 |
--- |
|
H |
57,500 |
9.1 |
atorvastatin |
- If you only have a G100 column, could you separate G and H? Explain your answer.
- Which resin would you use to separate D, E, and F? Explain your answer?
- Draw and label the chromatogram for the separation of D, E, and F.
Contributors and Attributions
- Garland Crawford (Crawford_gl@mercer.edu) and Kathryn Kloepper (kloepper_kd@mercer.edu), Mercer University
- Some portions of this module are adapted from the Separation Science unit by Tom Wenzel on the ASDL active learning site: https://community.asdlib.org/activelearningmaterials/separation-science/
- Sourced from the Analytical Sciences Digital Library


