Skip to main content
Chemistry LibreTexts

Acid-Base Chemistry

  1. Last updated
  2. Save as PDF
  • Page ID
    282012

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Monoprotic Acids and Bases

    Learning Objectives

    Following this activity, students should be able to:

    • Recall basic calculations and definitions about acid-base chemistry.
      • Interpret the pH scale and use Kw to draw relationships between [H+] and [OH-].
      • Write reactions represented by Ka and Kb for monoprotic acids.
      • Interpret the magnitudes of Ka and Kb.
      • Identify conjugate acid-base pairs.
      • Calculate the pH of strong acid, strong base, weak acid and weak base solutions
    • Determine when using the quadratic formula is necessary to determine the pH of a solution.
    • Find the fractions of association for weak acids and weak bases

    Based on your recollection of general chemistry…

    1. An important value in pH calculations is Kw. What reaction does this constant represent and what is the equilibrium constant expression for Kw?




     

    1. Kw = 1.0 × 10-14 at 25°C. Use the equilibrium constant expression for Kw above to derive a relationship between pH and pOH. Recall pH = -log[H+] and pOH = -log [OH-].




     

    1. Kw allows us always to relate [H+] to [OH-] and vice versa. In other words, if you know one of these, you can use Kw to find the other. Use Kw to complete the table.

    pH

    [H+]

    pOH

    [OH-]

    Circle one:

     

     

    8.14

     

    Acidic     Basic

     

    1.67 × 10-7

     

     

    Acidic     Basic

    10.35

     

     

     

    Acidic     Basic

     

     

     

    6.84 × 10-3

    Acidic     Basic
    1. Use Kw to show that a neutral solution has pH = 7.

     

     

    1. Which statement accurately compares a pH 4 and pH 2 solution?
      1. A solution with pH = 4 is 100 times more acidic than a solution with pH = 2.
      2. A solution with pH = 4 is two times as acidic as one with pH = 2.
      3. A solution with pH = 4 is half as acidic as one with pH = 2.
      4. A solution with pH = 4 has only 1% as much H+ as a pH 2 solution.
         
    2. Calculations involving acids
      1. Compare the approach you would use when calculating the pH of a strong acid solution to that of a weak acid. What piece of information do you need for a weak acid problem that you do not need for a strong acid?




         

      2. Write the reaction represented by the Ka of a weak acid. Use “HA” as a generic weak acid.


         

      3. Consider a problem that says, “Calculate the pH of a solution of the weak acid HA with a concentration of F,” where “F” is the given concentration of the acid. (F is used to represent the “formal” concentration of an acid before it dissociates in water.) Make a generic ICE table that would work for any weak acid problem, using x = [H+] = [A-]. You should be able to come with a “go to” equation that allows you to skip the ICE chart most of the time.






         

      4. Sometimes pKa is used in place of Ka. How is pKa calculated?


         

      5. Compare an acid with a pKa of 2 to one with a pKa of 5. Which is the stronger acid?





     

    1. Calculations involving bases
      1. List some strong bases. What type of ionic compounds act as strong bases?





         

      2. How do you calculate the pH of a strong base solution? What extra step is necessary relative to a strong acid?



         

      3. Briefly describe the steps to find the pH of a weak base. Compare the calculation to that of a weak acid and similarly come up with a reasonable “go to” equation. What is “x” equal to in this case?





         

      4. Often only Ka’s can be readily found tabulated in reference texts. How do you find Kb for a weak base when only weak acid Ka’s are provided?


         

      5. The relationship between Ka and Kb is only true for conjugate acid-base pairs. How do you recognize a conjugate acid-base pair? Give one example.

         

      6. Use Appendix B* (p. 538 – 545) to find Kb for the following weak bases.

        Weak Base

        Kb

        Name

        Formula

        Potassium acetate

        KCH3COO

         

        Ammonia

        NH3

         

        Sodium fluoride

        NaF

         

        *A note about using Appendix B: The name written is for the uncharged molecule and the structure provided shows the fully protonated form of the molecule. Because acids and bases are often charged molecules, they often exist as salts with a counter cation (usually Na+ or K+) or anion (usually Cl-) that is only there to balance the charge. These ions are not themselves acids or bases and therefore can be ignored in pH calculations.

      7. Pick one of the acid-base pairs in the table above to show that KaxKb = Kw. Recall that when you “add up” individual equilibrium reactions, you multiply their K’s.





     

     

    Find the pH…

    1. Now apply what you have brushed up on to determine the pH of the following solutions. Classify each as a strong acid, strong base, weak acid and weak base.

      Solution

      Circle one:

      Calculation*

      pH**

      1.7 × 10-4 M HCl

      Strong acid

      Weak acid

      Strong base

      Weak base

       

       

       

       

      0.025 M (CH3CH2)2NH (diethylamine)

      Strong acid

      Weak acid

      Strong base

      Weak base

       

       

       

       

       

      0.10 M NH4Cl

      (ammonium chloride)

      Strong acid

      Weak acid

      Strong base

      Weak base

       

       

       

       

       

      0.0035 M Ba(OH)2

      Strong acid

      Weak acid

      Strong base

      Weak base

       

       

       

       

      * A common headache in these calculations is having to use the quadratic formula to solve for an unknown (x). As long as K << F (by a factor of 105), we can usually ignore x in such a way that the quadratic formula can be avoided.

      **Recall that for numbers on a log scale like pH, only digits after the decimal point are considered significant.

     

    1. The fraction of dissociation (\(\alpha\)) for weak acids represents fraction of a total concentration (F) of an acid (HA) is deprotonated (A-) in solution. Sometimes percent dissociation is used in place of \(\alpha\) and is simply \(\alpha\) × 100%.
      1. Using “x” for the concentration of the deprotonated acid (A-), write an equation for \(\alpha\).




         

      2. Find \(\alpha\) for benzoic acid solutions with the following concentrations: 0.10 M (see your calculation above), 1.0 × 10-3 M and 1.0 × 10-5 M.






         

      3. Sketch how \(\alpha\) changes with concentration. Look carefully at how the axes in the graph below are labeled.

        Graph_FractionOfDissociation.png

      4. Based on your figure above, what happens to a weak acid solution when it is diluted?
        1. When a weak acid is diluted, the pH stays constant.
        2. When a weak acid is diluted, more of the acid is protonated.
        3. When a weak acid is diluted, more of the acid is deprotonated.
        4. When a weak acid is diluted, the portion that is protonated stays constant.
           
      5. Similarly, the fraction of association (also represented by \(\alpha\)) can be calculated for weak bases. Find \(\alpha\) for a 0.023 M NH3 (ammonia).



     

     

    Polyprotic Acids and Bases

    1. Find the pH of the following solutions. Phosphoric acid (H3PO4) is a triprotic acid with pKa1 = 2.148, pKa2 = 7.198 and pKa3 = 12.375.

    A solution of…

    …has a pH of…

    1.0 M H3PO4

     

     

     

     

     

     

     

    1.0 M Na3PO4

     

     

     

     

     

     

     

     

    1.0 M Na2HPO4

     

     

     

     

     

     

     

    1.0 M NaH2PO4

     

     

     

     

     

     

     

     

     
    1. Find the pH of the following buffer solutions. Use the information about phosphoric acid above.

    A solution containing equal concentrations of…

    …has a pH of…

    NaH2PO4 and H3PO4

     

     

     

     

    NaH2PO4 and Na2HPO4

     

     

     

     

    Na2HPO4 and Na3PO4

     

     

     

     

     

    1. The fully protonated form of the amino acid cysteine is shown below with its corresponding pKa’s. Draw the dominant form of cysteine at each given pH.

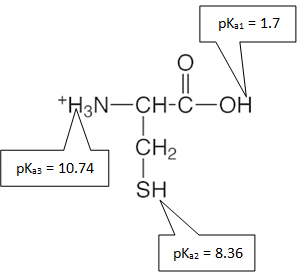
    Cysteine.png

    At a pH of…

    …the dominant form of cysteine is..

    7.00

     

     

     

     

     

     

    8.00

     

     

     

     

     

     

    9.00

     

     

     

     

     

     

    11.00

     

     

     

     

     

     

    Contributors and Attributions

     
     
     
     
     
     
     
     
     

    This page titled Acid-Base Chemistry is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Contributor via source content that was edited to the style and standards of the LibreTexts platform.