Resonance Theory

Chemists use Lewis diagrams to depict structure and bonding of covalent entities, such as molecules and polyatomic ions, henceforth, molecules. eg:

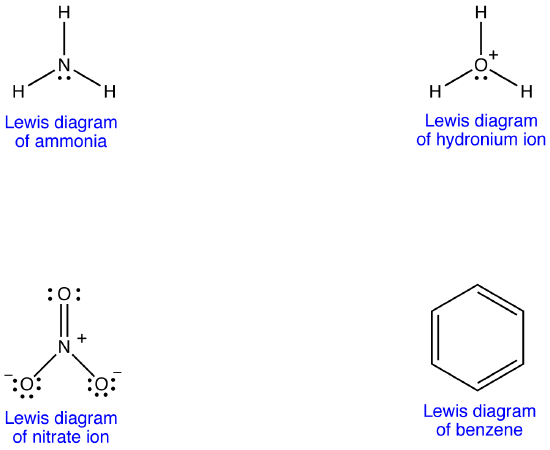
The Lewis diagram of many a molecule, however, is not consistent with the observed properties of the molecule.

Example 1: Nitrate Ion

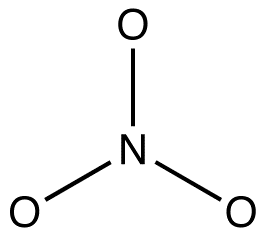
The nitrate ion, according to its Lewis diagram, has two types of nitrogen-oxygen bonds, one double bond and two single bonds, suggesting that one nitrogen-oxygen bond in the nitrate ion is shorter and stronger than each of the other two. Also, the Lewis structure implies, with respect to formal charge, that there are two types of oxygen atoms in the nitrate ion, one formally neutral and each of the other two bearing a formal charge of –1. Experimentally, however, the three nitrogen-oxygen bonds in the nitrate ion have the same bond length and the same bond energy, and the three oxygen atoms are indistinguishable. The Lewis diagram fails to explain the structure and bonding of the nitrate ion satisfactorily.

Two additional Lewis diagrams can be drawn for the nitrate ion.

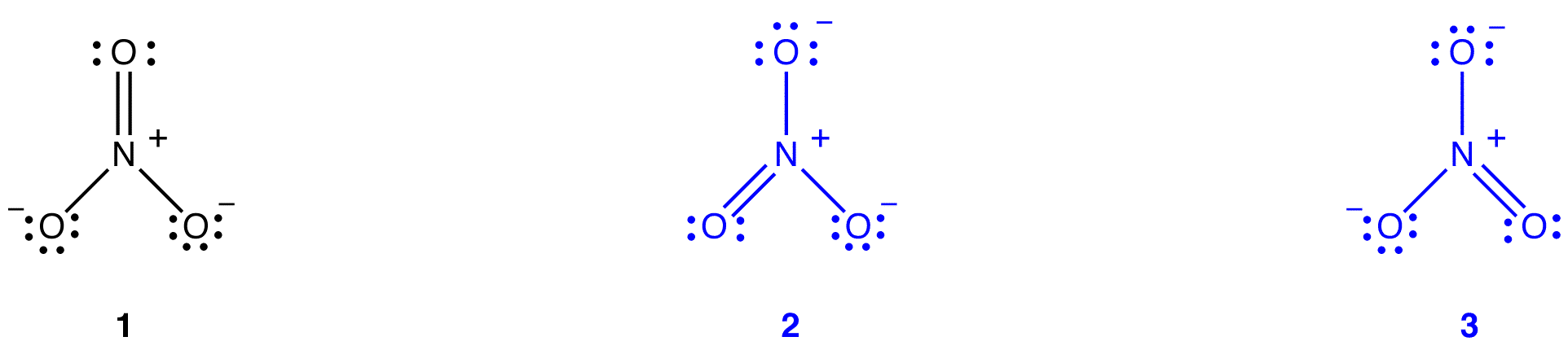
However, none of them are consistent with the observed properties of the nitrate ion and, therefore, does not correctly depict the nitrate ion.

Example 2: Benzene

Benzene, according to its Lewis diagram, has two types of carbon-carbon bonds, three double bonds and three single bonds, suggesting that each of three carbon-carbon bonds in benzene is shorter and stronger than each of the other three. Experimentally, however, the six carbon-carbon bonds in benzene have the same bond length and the same bond energy. The Lewis diagram fails to explain the structure and bonding of benzene satisfactorily.

An attribute of molecules of which the classical Lewis diagram is not consistent with the observed properties is that other valid Lewis diagrams can be generated for them. One additional Lewis diagram can be drawn for benzene.

However, none of them are consistent with the observed properties of benzene and, therefore, does not correctly depict benzene.

Resonance theory is an attempt to explain the structure of a species, like the nitrate ion or benzene, no Lewis diagram of which is consistent with the observed properties of the species. The major advantage of resonance theory is that, although based on rigorous mathematical analysis, resonance theory can be applied successfully invoking little or no math. Resonance theory is explained below using the nitrate ion as the example.

According to resonance theory, the structure of the nitrate ion is not 1 nor 2 nor 3 but the average of all three of them, weighted by stability. Lewis diagrams 1, 2, and 3 are called resonance forms, resonance structures, or resonance contributors of the nitrate ion. The structure of the nitrate ion is said to be a resonance hybrid or, simply, hybrid of resonance forms 1, 2, and 3. Whenever it is necessary to show the structure of the nitrate ion, resonance forms 1, 2, and 3 are drawn, connected by a double-headed arrows.

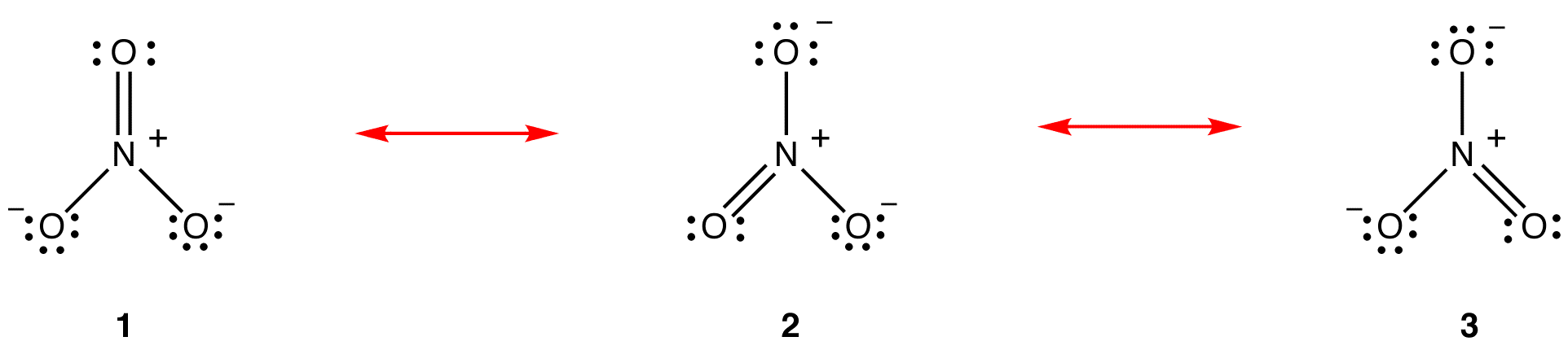
The three resonance forms of the nitrate ion, 1, 2, and 3, are identical, so they have the same stability and, therefore, contribute equally to the hybrid. Since the exact extent to which each resonance form of the nitrate ion contributes to the hybrid is known, the bond order of each nitrogen-oxygen bond as well as the formal charge on each oxygen atom in the hybrid can be easily determined:

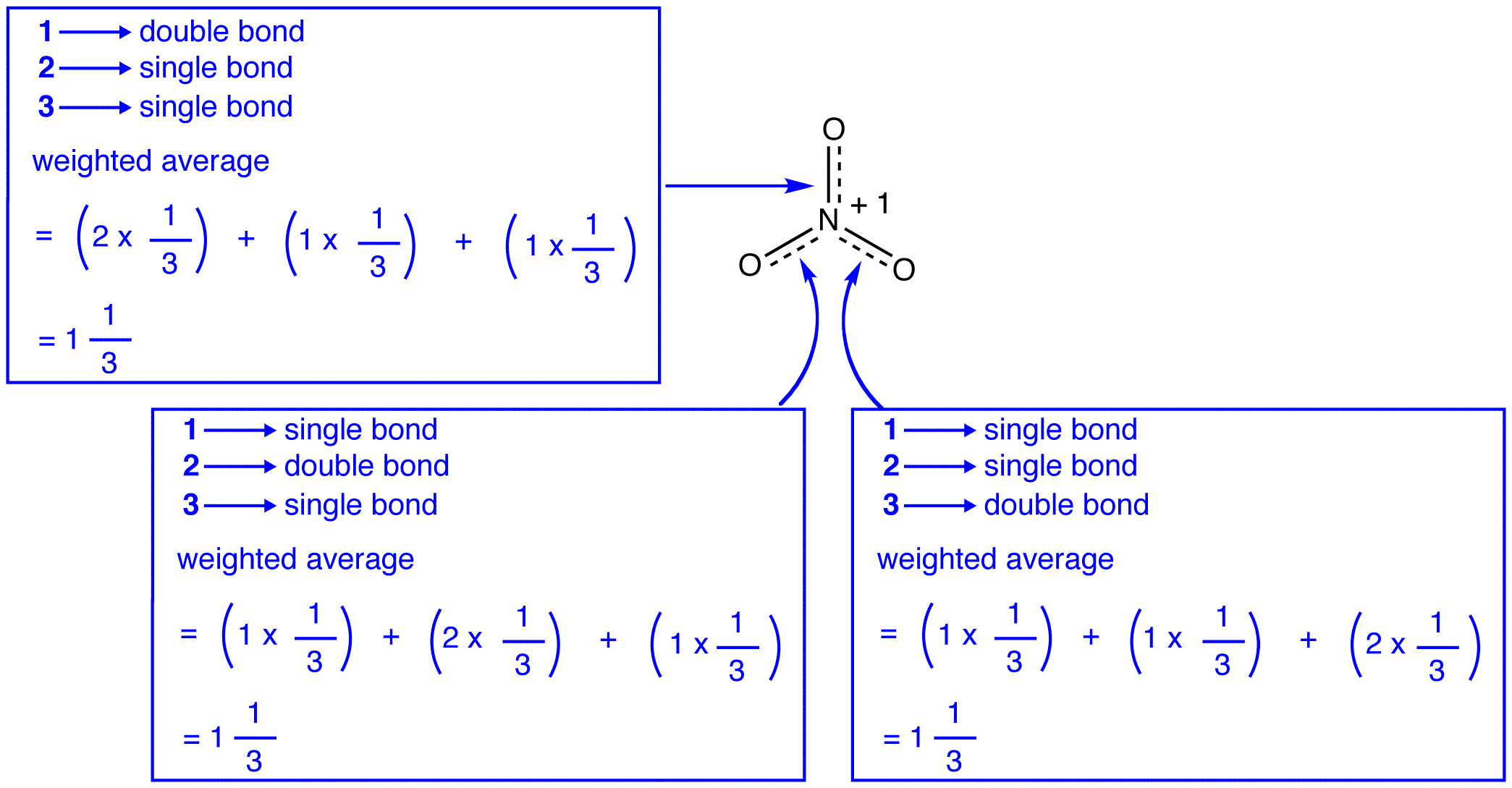
According to resonance theory, each bond in the nitrate ion is one and one-third of a bond, which is consistent with the observation that the three bonds in the nitrate ion have the same bond length and the same bond energy.

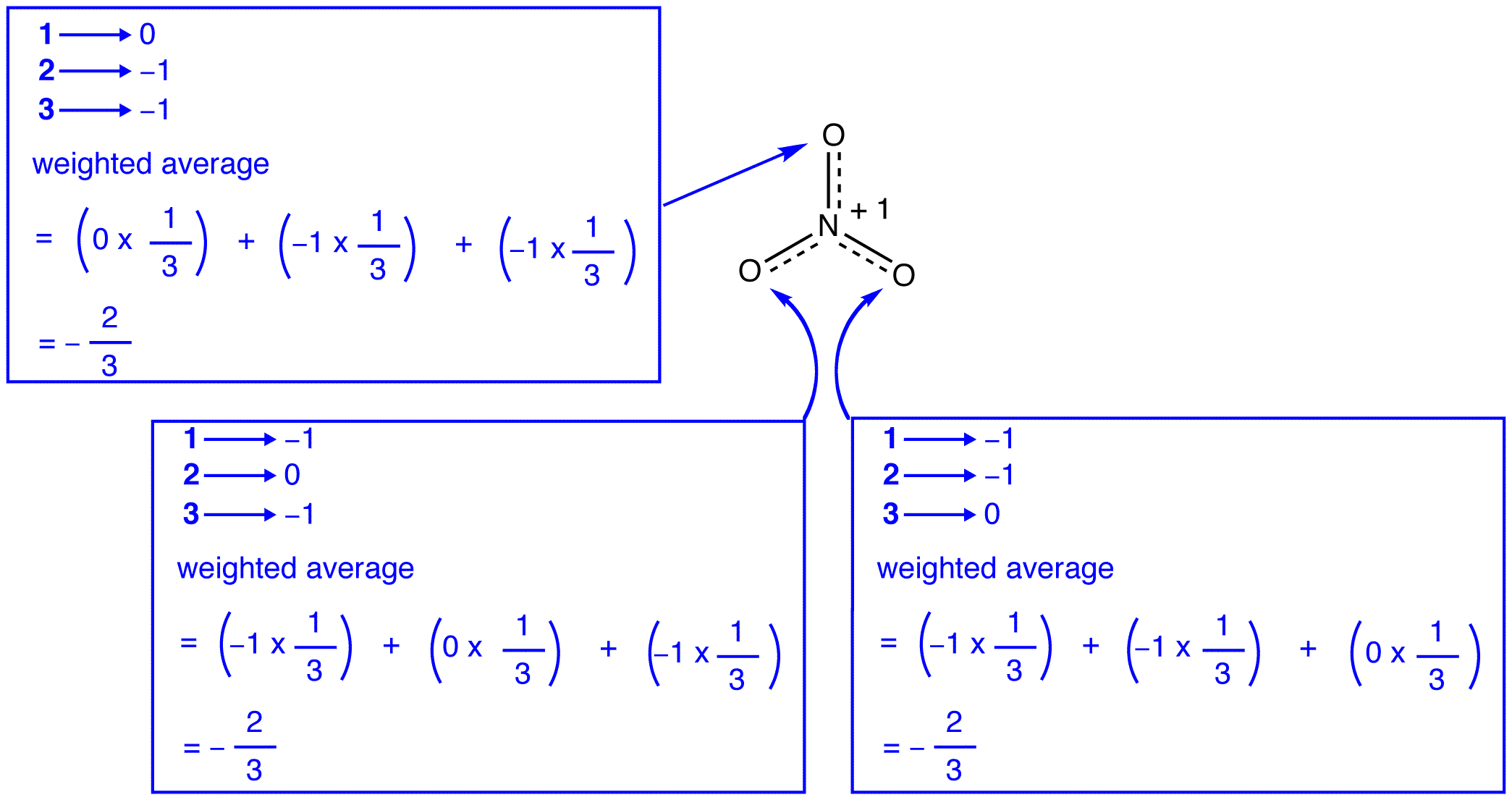
According to resonance theory, each oxygen atom in the nitrate ion has a formal charge of –2/3, which, in conjunction with the fact that the three nitrogen-oxygen bonds are identical, is consistent with the observation that the three oxygen atoms in the nitrate ion are indistinguishable.

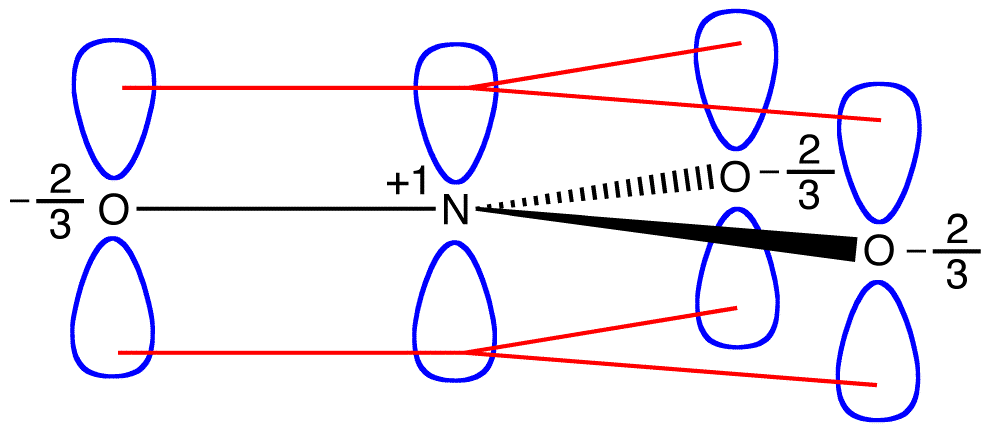
In each resonance form of the nitrate ion, there are two pi electrons, and they are shared only by two atoms. An electron shared only by two atoms is said to be localized. Thus, the two pi electrons in each resonance form of the nitrate ion are localized. The nitrate ion, as represented by the hybrid, has two pi electrons:

# electrons in one pi bond = 2

# electrons in one-third of a pi bond = 2/3

# electrons in three of them = 3 x (2/3) = 2

The two pi electrons in the nitrate ion are shared by a total of four atoms, one nitrogen atom and three oxygen atoms. An electron shared by more than two atoms is said to be delocalized. Thus, the two pi electrons in the nitrate ion are delocalized. Delocalization of pi electrons in the nitrate ion requires that the four atoms be on the same plane, allowing lateral overlap of the p orbitals on them.

If the energy of the nitrate ion were the weighted average of the energies of its three resonance forms, just as the structure of the nitrate ion is the weighted average of the structures of its three resonance forms, it should be equal to the energy of one of the three identical resonance forms:

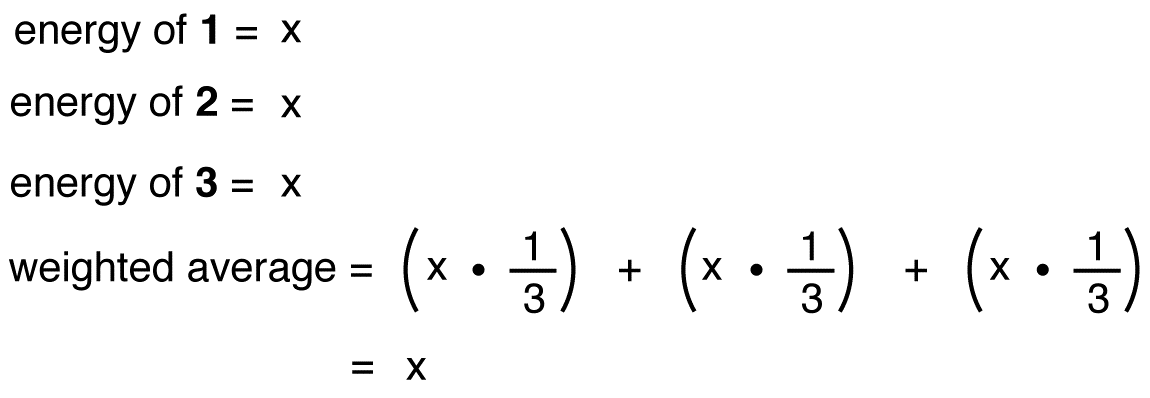
If the energy of the hybrid were equal to that of a resonance form, given that all chemical entities (elementary particles, atoms, molecules, etc.) naturally tend to be in the lowest possible energy state, there would be no advantage for the nitrate ion to exist as the hybrid; it could simply exist as a resonance form. Since the nitrate ion exists as the hybrid, not as a resonance form, it can be inferred that the energy of the hybrid is lower than that of any of the resonance forms.

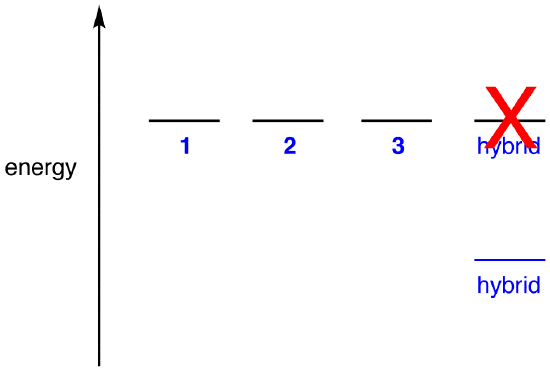
According to resonance theory then, the energy of a molecule is lower than that of the lowest-energy resonance form. Since the nitrate ion has lower energy and, therefore, is more stable than any of its resonance forms, the nitrate ion is said to be resonance stabilized.

There are two misconceptions about resonance theory among beginning students, likely due to literal interpretation of the word resonance. They are described below, using the nitrate ion as the example.

Misconception 1: The nitrate ion exists as resonance form 1 for a moment and then changes either to resonance form 2 or to resonance form 3, which interconvert, or revert to 1.

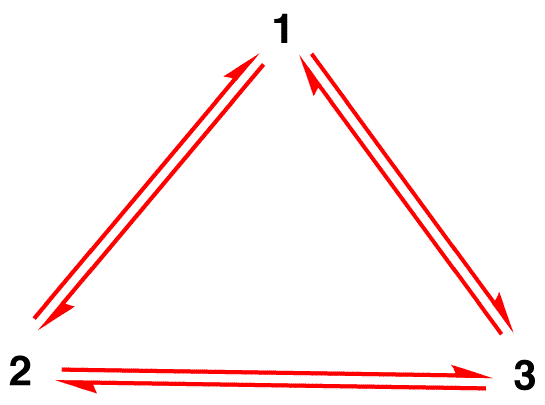
The structure of the nitrate ion is not 1 nor 2 nor 3 but the hybrid and does not change with time unless undergoing a reaction.

Misconception 2: In a sample of nitrate ions, at a given moment, one-third of the ions exist as resonance form 1, another one-third as resonance form 2, and the remaining one-third as resonance form 3.

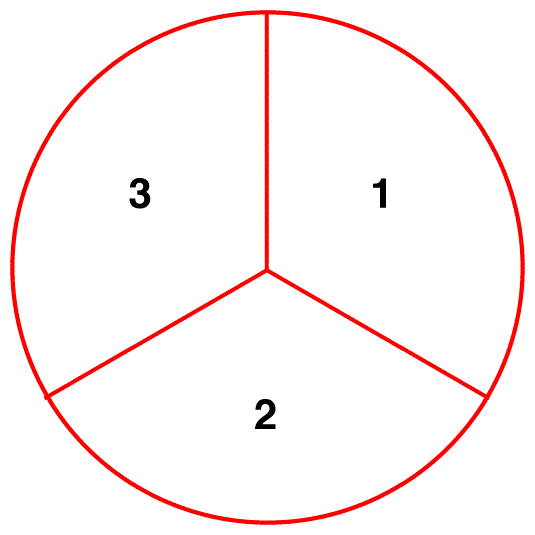
In a sample of nitrate ions, at a given moment, all ions have the same structure, which is the hybrid.

The classic analogy used to clarify these two misconceptions is the mule (Morrison, R. T.; Boyd, R.N. Organic Chemistry, fifth edition; Allyn and Bacon: Boston, 1987, pg. 373). Biologically, a mule is a hybrid of a horse and a donkey. This does not mean that a mule resembles a horse for a moment and then changes to resemble a donkey. The appearance of a mule is a combination of that of a horse and that of a donkey and does not change with time. Nor does it mean that, in a herd, some mules resemble a horse and the others a donkey. In a herd, all mules have the same appearance, which is a combination of a horse and a donkey. The weakness of this analogy is that horses and donkeys do exist, whereas resonance forms are strictly hypothetical. A better analogy, cited in Morrison and Boyd, is the rhinoceros. Upon seeing a rhinoceros, one could describe it as the hybrid of a dragon and a unicorn, two creatures that do not exist.

Rules for Drawing Resonance Forms

1. Resonance forms are Lewis diagrams, which are based on valence bond theory.They must, therefore, obey the basic rules of valence bond theory. Thus, hydrogen can not have more than two valence electrons; Period-two elements can not have more than eight valence electrons; elements in Period three and below may have more than eight valence electrons. eg: In each resonance form of the nitrate ion, there are two elements, nitrogen and oxygen, which are Period-two elements. In none of the resonance forms of the nitrate ion are there more than eight valence electrons on any of the atoms.

2. All resonance forms must have the same sigma-bond framework, differing only in the locations of pi electrons and nonbonded valence electrons. eg: All three resonance forms of the nitrate ion have the same sigma-bond framework:

They differ from one another only in the locations of pi electrons and lone pairs.

Organic chemists increasingly violate this rule in order to explain the structures of reactive intermediates as resonance-stabilized species. eg: oxymercuration

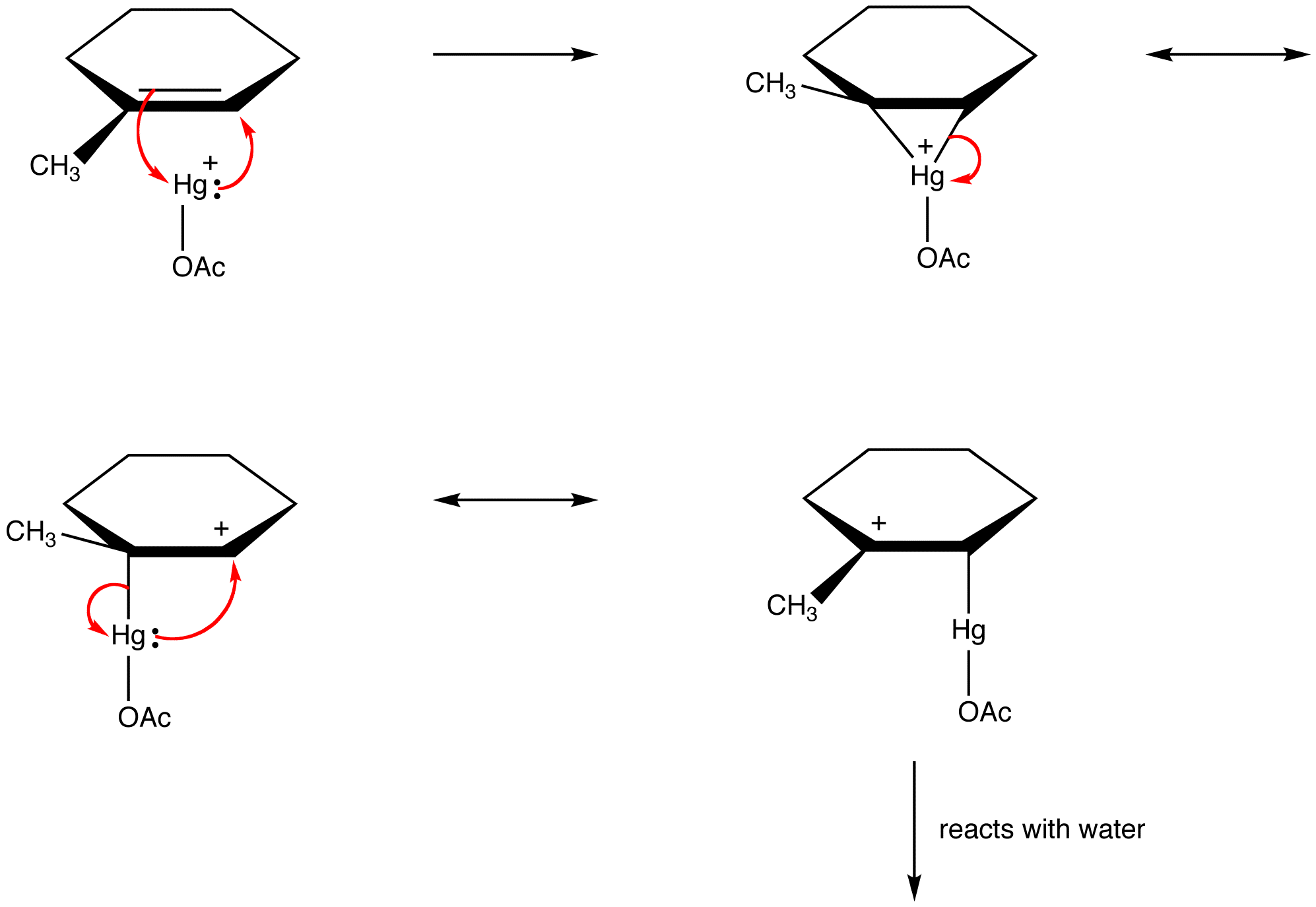
Determination of Relative Contribution of Resonance Forms to the Hybrid

The three forms of the nitrate ion are identical and, therefore, have the same stability. Consequently, they contribute equally to the hybrid. The resonance forms of most resonance-stabilized molecules are different from each other, so they do not contribute equally to the hybrid. The more stable the resonance form, the more it contributes to the hybrid. Thus, the determination of relative contribution or resonance forms to the hybrid requires the determination of their relative stability. Use the following rules to determine the relative stability of resonance forms.

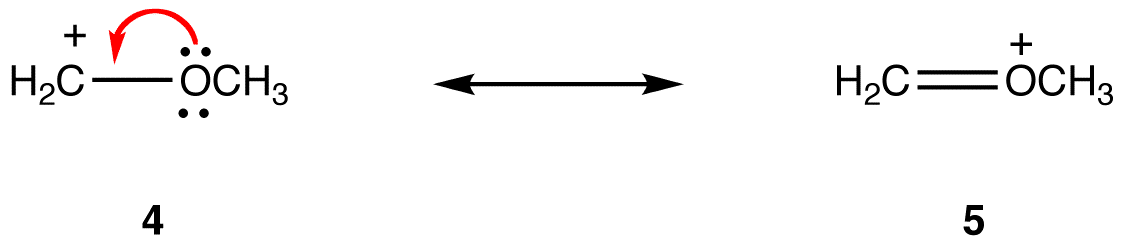
Rule 1: A resonance form in which all atoms have an octet of valence electrons is more stable than one in which at least one atom does not. eg: In resonance form 5, all atoms have an octet of valence electrons; in 4, one atom, the carbon atom bearing the formal charge of +1, does not. Thus, resonance form 5 is more stable than resonance form 4.

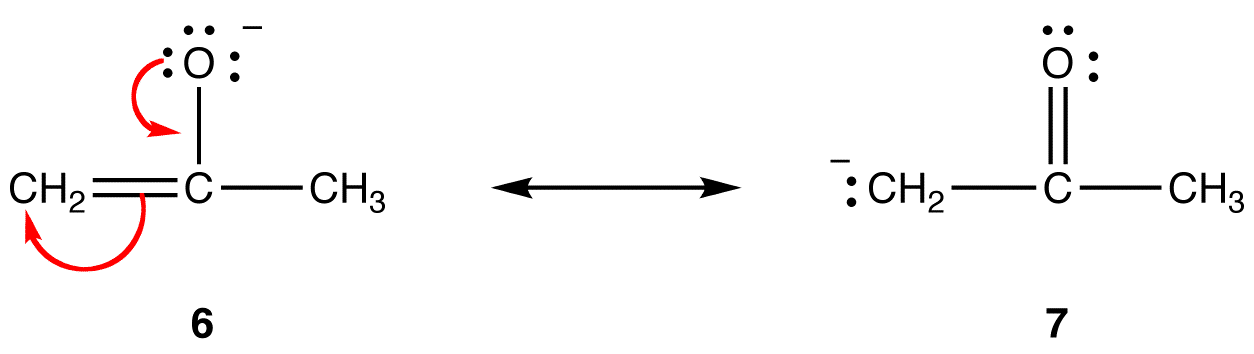
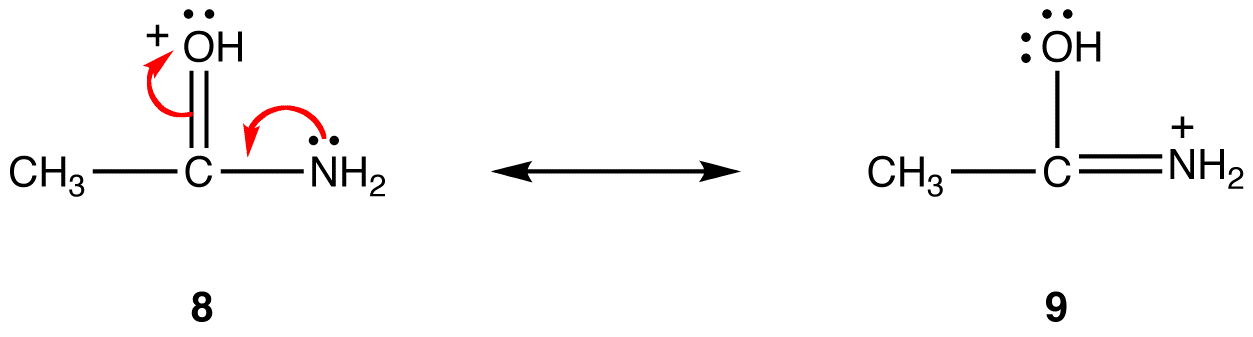
Rule 2: All else being equal, a resonance form that has a formal negative charge on a more electronegative atom is more stable than one that has a formal negative charge on a less electronegative atom. eg: In resonance form 6, the formal negative charge is on an oxygen atom; in 7, it is on a carbon atom. Oxygen is more electronegative than carbon. Thus, resonance form 6 is more stable than resonance form 7. The trend is opposite with respect to formal positive charges. All else being equal, a resonance form that has a formal positive charge on a less electronegative atom is more stable than one that has a formal positive charge on a more electronegative atom. eg: In resonance form 8, the formal positive charge is on an oxygen atom; in 9, it is on a nitrogen atom. Nitrogen is less electronegative than oxygen, Thus, resonance form 9 is more stable than resonance form 8.

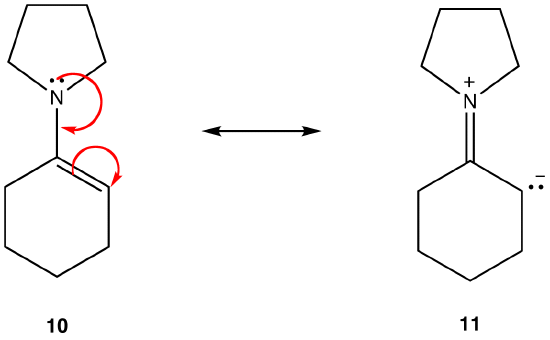
Rule 3: All else being equal, a resonance form that does not have a charge separation, called a dipolar resonance form, is more stable than one that does. eg: Resonance form 11 is a dipolar resonance form; 10 is not. Thus, 10 is more stable than 11. This rule is a consequence of the vector form of Coloumb’s law, according to which opposite charges attract. The corollary is that, to keep opposite charges separated, energy is required, meaning that 11 has higher energy than 10, so 10 is more stable than 11.

Rule 4: In dipolar resonance forms, all else being equal, the greater the distance between separated charges, the more stable the resonance form. eg: Both resonance forms 12 and 13 are dipolar resonance forms. The distance between the separated charges is greater in 13 (three bonds) than in 12 (one bond), so 13 is more stable than 12. This rule is a consequence of the scalar form of Coloumb’s law, which states that the attractive force between opposite charges is inversely proportional to the square of the distance between them. Thus, the energy required to keep the opposite charges separated in 12 is higher than that in 13, meaning that 12 has higher energy than 13, so 13 is more stable than 12.

The above rules may not apply to resonance involving elements of Period three and below, due to their ability to accommodate more than eight electrons in the valence shell. eg:

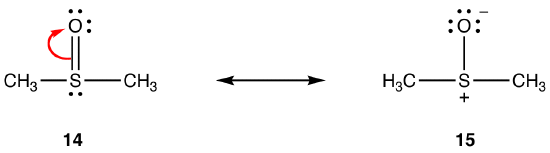
The double bond in 14 consists of a sigma bond and a bond formed by the overlap of a 2p orbital, bearing two electrons, in the oxygen atom and an empty 3d orbital in the sulfur atom. These two orbitals have very different energies, sizes, and shapes, so the overlap between them, known as a pπ–dπ interaction, is weak. Consequently, there is little double bond character in the sulfur-oxygen bond in the hybrid, i.e., 15 is the major resonance form.

• Gamini Gunawardena from the OChemPal site (Utah Valley University)

Template:HideTOC