Hybridization

Last updated
Save as PDF

Page ID: 40468

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The original valence bond theory, as proposed by G.N. Lewis, is inadequate in explaining bonding and structure of many a covalent species. Hybridization is a model that attempts to remedy the shortcomings of simple valence bond theory. Below, the concept of hybridization is described using four simple organic molecules as examples.

eg. 1: methane

Experimentally, methane contains two elements, carbon and hydrogen, and the molecular formula of methane is CH₄. Both carbon and hydrogen are non-metals, implying that methane is a covalent compound, not an ionic compound, meaning methane is made up of molecules, not ions. According to valence bond theory, the structure of a covalent species can be depicted using a Lewis structure. The Lewis structure of methane is 1, which shows that there are four carbon-hydrogen bonds in the methane molecule.

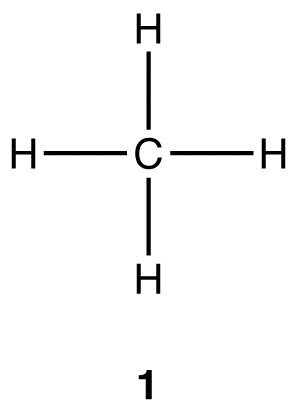
Experimentally, the four carbon-hydrogen bonds in the methane molecule are identical, meaning they have the same bond energy and the same bond length. VSEPR theory suggests that the geometry at the carbon atom in the methane molecule is tetrahedral (2), and there exists a large body of both theoretical and experimental evidence supporting this prediction.

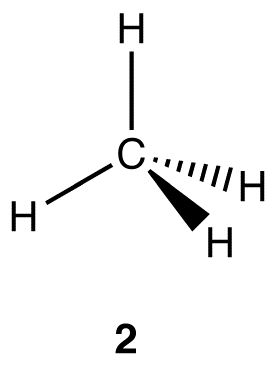
According to valence bond theory, to form a covalent bond, a valence orbital bearing one electron in one atom overlaps with a valence orbital bearing one electron in another atom. Consider the electron configurations of carbon and hydrogen.

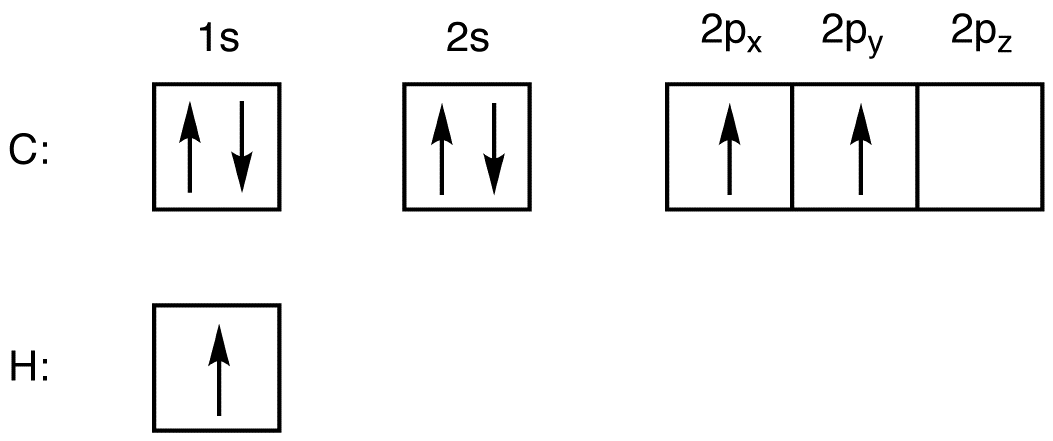
The valence shell in carbon is shell two, and it has four electrons. The number of valence orbitals in carbon each bearing one electron is two (2p_x and 2p_y). The valence shell in hydrogen is shell one, which has one orbital (1s), bearing one electron. Thus, the maximum number of hydrogen atoms a carbon atom can form covalent bonds with is two, not four, leading to 3, which would be unstable because the carbon atom lacks an octet of valence electrons.

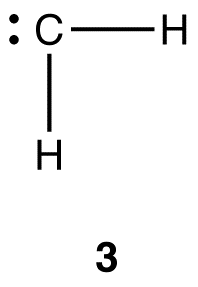
Notice that the simple valence bond theory fails even to explain the existence of methane. To explain the structure of the methane molecule, two modifications, known as excitation and hybridization, are introduced to valence bond theory.

1. Excitation

The carbon atom used to generate 3 is a ground-state atom. Convert it into an excited-state atom by moving an electron from the 2s orbital to the empty 2p_z orbital. Since the latter has higher energy than the former, this change requires energy.

In the excited-state carbon atom, there are four valence orbitals each bearing one electron (2s, 2p_x, 2p_y, and 2p_z). Thus, the excited-state carbon atom can form covalent bonds with four hydrogen atoms, resulting in a methane molecule (4).

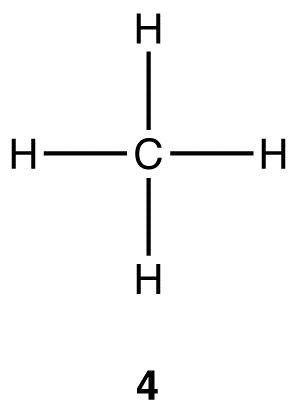
There are, however, two aspects of 4 that are not consistent with observations:

i. As noted earlier, experimentally, the four carbon-hydrogen bonds in the methane molecule are identical. In 4, however, there are two types of carbon-hydrogen bonds, the one formed by the overlap of the 2s orbital of the carbon atom with the 1s orbital of a hydrogen atom and each of the other three formed by the overlap of a 2p orbital of the carbon atom with the 1s orbital of a hydrogen atom.

ii. As noted earlier, the tetrahedral geometry at the carbon atom in the methane molecule is established unequivocally. In 4, three of the four carbon hydrogen bonds would be perpendicular to one another because the three 2p orbitals in the excited-state carbon atoms are, implying that, in 4, the geometry at the carbon is not tetrahedral.

2. Hybridization

Place the four valence orbitals in the excited-state carbon atom used to generate 4 on a one-dimensional graph in which the single dimension is energy.

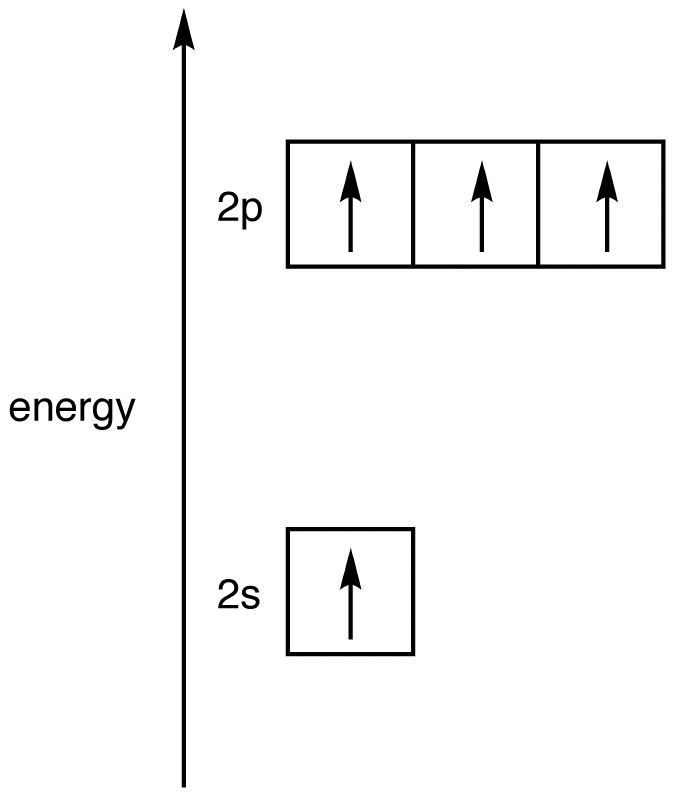
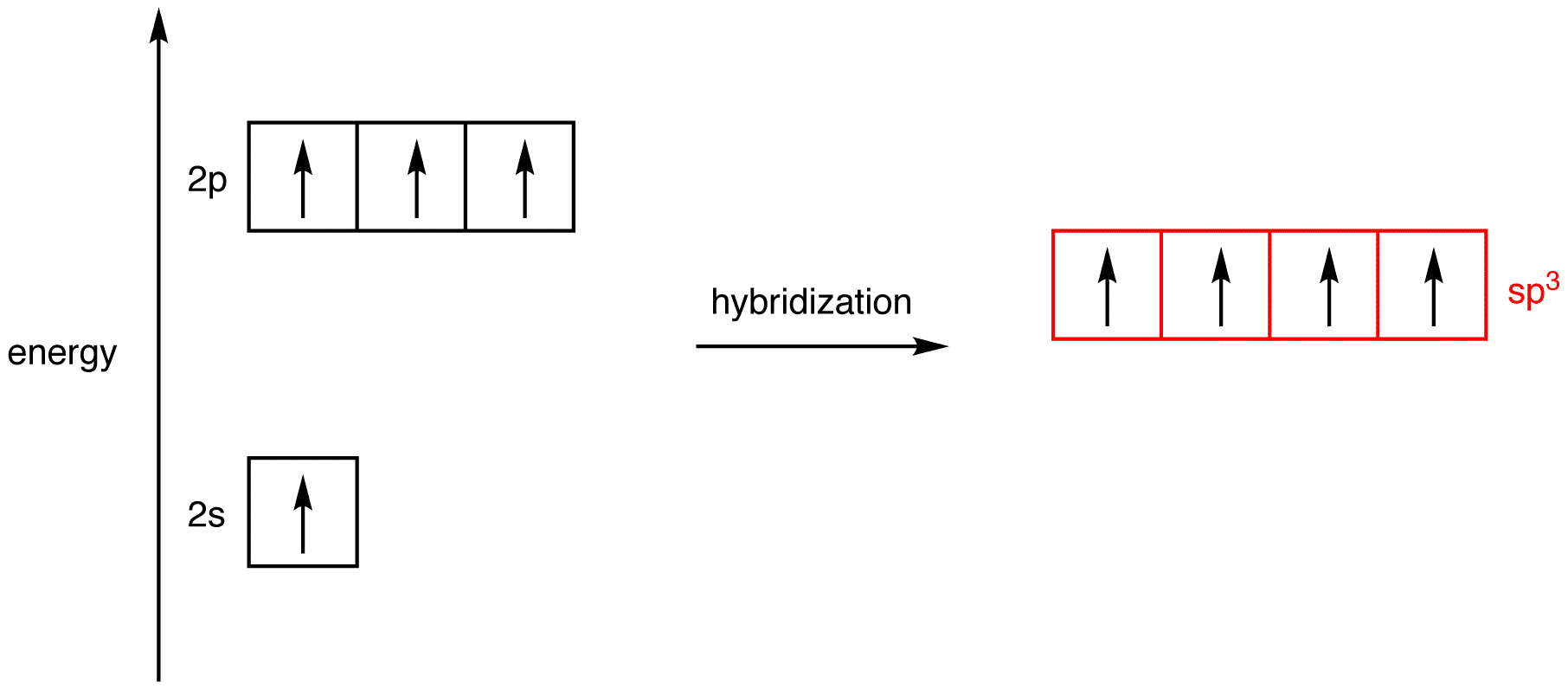
Imagine mixing the 2s orbital and the three 2p orbitals to give a homogeneous mixture and, then, dividing the mixture into four new, identical orbitals. This process is known as hybridization, and the four new, identical orbitals are called hybridized orbitals. Since the four hybridized orbitals are created by mixing one 2s orbital and three 2p orbitals, they are called sp³-hybridized orbitals, and the energy of an sp³-hybridized orbital, on the graph, falls between those of a 2s orbital and a 2p orbital, closer to that of a 2p orbital. The four atomic orbitals used in hybridization had a total of four electrons, which are to be distributed in the four sp³-hybridized orbitals. Since the four sp³-hybridized orbitals have the same energy, according to Hund’s rule, the electrons must be equally distributed in them.

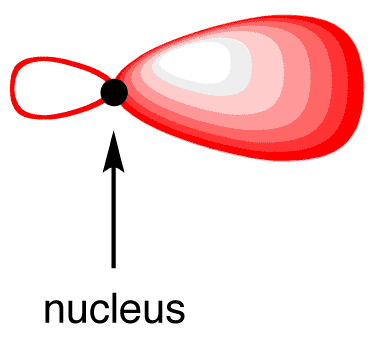
The shape of the sp³-hybridized orbital is shown mathematically to be roughly as follows.

Each sp³-hybridized orbital bears an electron, and electrons repel each other. To minimize the repulsion between electrons, the four sp³-hybridized orbitals arrange themselves around the carbon nucleus so that they are as far away as possible from each other, resulting in the tetrahedral arrangement of the four sp³-hybridized orbitals around the carbon nucleus (5). The carbon atom 5 is called an “sp³-hybridized carbon atom.”

The overlap of each sp³-hybridized orbital in 5 with the 1s orbital of a hydrogen atom leads to a methane molecule (6).

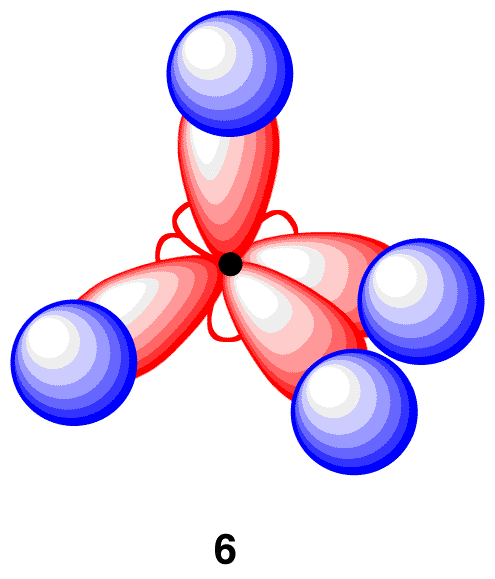
In 6, each of the four carbon-hydrogen bonds is formed by the same overlap: sp³(C)-1s(H). As such, the four carbon-hydrogen bonds in 6 are identical, consistent with observations. Also in 6, the geometry at the carbon atom is tetrahedral, consistent with VSEPR theory. In summary, to explain the bonding in the methane molecule using the valence bond model, two modifications are necessary.

i. Use and excited-state carbon atom, rather than a ground-state carbon atom, in bonding.

ii. Use an sp³-hybridized carbon atom in bonding.

eg. 2: ethane

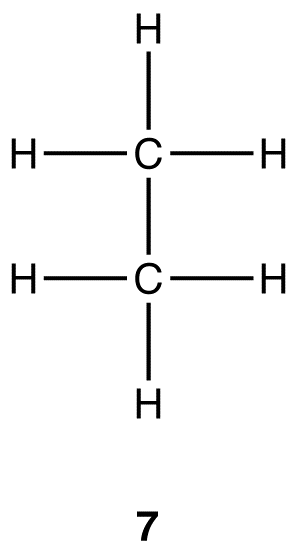
Experimentally, ethane contains two elements, carbon and hydrogen, and the molecular formula of ethane is C₂H₆. Like methane, ethane a covalent compound. The Lewis structure of ethane is 7, which shows that there are one carbon-carbon bond and six carbon-hydrogen bonds in the ethane molecule.

Experimentally, the six carbon-hydrogen bonds in the ethane molecule are identical. According to VSEPR theory, the geometry at each carbon atom in the ethane molecule is tetrahedral (8).

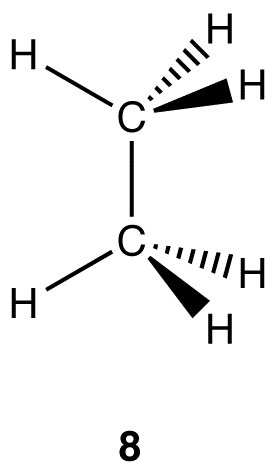
There are two similarities between the molecules of methane and ethane.

i. In each molecule, the coordination number of a carbon atom is four.

ii. In each molecule, the geometry at a carbon atom is tetrahedral.

The implications is that, to explain the bonding in the ethane molecule using the valence bond model, two modifications are necessary.

i. Use and excited-state carbon atom, rather than a ground-state carbon atom, in bonding.

ii. Use two sp³-hybridized carbon atoms in bonding.

eg. 3: ethylene

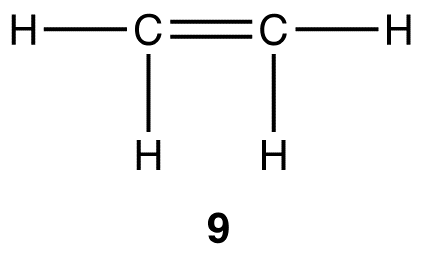
Experimentally, ethylene contains two elements, carbon and hydrogen, and the molecular formula of ethylene is C₂H₄. Like methane and ethane, ethylene is a covalent compound. The Lewis structure of ethylene (9) indicates that there are one carbon-carbon double bond and four carbon-hydrogen bonds in the ethylene molecule.

Experimentally, the four carbon-hydrogen bonds in the ethylene molecule are identical. According to VSEPR theory, the geometry at each carbon atom in the ethylene molecule is planar trigonal (10).

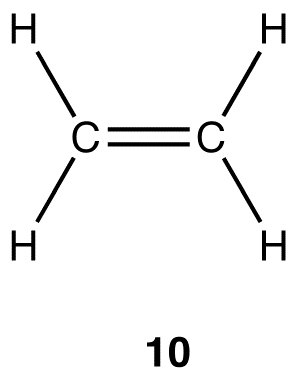
In the ethylene molecule, each carbon atom forms four bonds, implying that the ethylene molecule can not be constructed directly from two ground-state carbon atoms, for, as explained earlier, a ground-state carbon atom can form a maximum of only two bonds; only two excited-state carbon atoms can lead to an ethylene molecule. The coordination number of each carbon atom in the ethylene molecule is three, not four as is the case with the carbon atoms in methane and ethane, suggesting that the two carbon atoms in the ethylene molecule could not possibly be sp³-hybridized.

Imagine mixing the 2s orbital and two of the three 2p orbitals in an excited-state carbon atom thoroughly to give a homogeneous mixture and, then dividing the mixture into three new, identical orbitals, which are hybridized, specifically, sp²-hybridized, orbitals. Since the three sp²-hybridized orbitals are created by mixing one 2s orbital and two 2p orbitals, the energy of an sp²-hybridized orbital falls between those of a 2s orbital and a 2p orbital. The three atomic orbitals used in hybridization had a total of three electrons, which are to be distributed in the three sp²-hybridized orbitals equally, following the Hund’s rule.

The shape of the sp²-hybridized orbital is shown mathematically to be roughly the same as that of the sp³-hybridized orbital.

To minimize the repulsion between electrons, the three sp²-hybridized orbitals arrange themselves around the carbon nucleus so that they are as far away from each other as possible, leading to their planar trigonal arrangement.

The 2p orbital that did not participate in hybridization has one electron. Again, to minimize the repulsion between electrons, it positions itself so that is as far away as possible from each sp²-hybridized orbital, leading to the positioning of the 2p orbital perpendicular to each sp²-hybridized orbital 2(11). The carbon atom 11 is called an “sp²-hybridized carbon atom.”

In the ethylene molecule, each carbon atom is bonded to two hydrogen atoms. Thus, overlap two sp²-hybridized orbitals in 11 with the 1s orbitals of two hydrogen atoms (12).

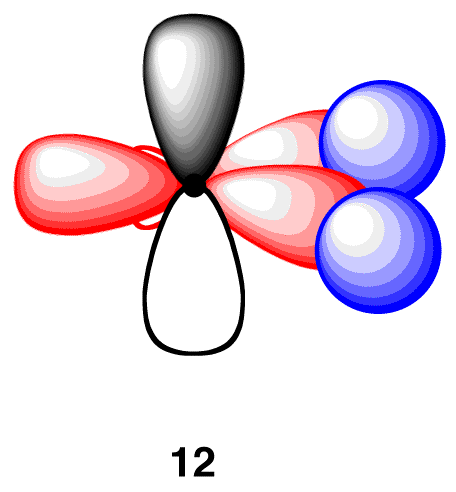
In the ethylene molecule, each carbon atom is bonded to the other carbon atom, in addition to two hydrogen atoms. Thus, take two units of 12 and overlap their sp²-hybridized orbitals, each bearing an electron, to give 13.

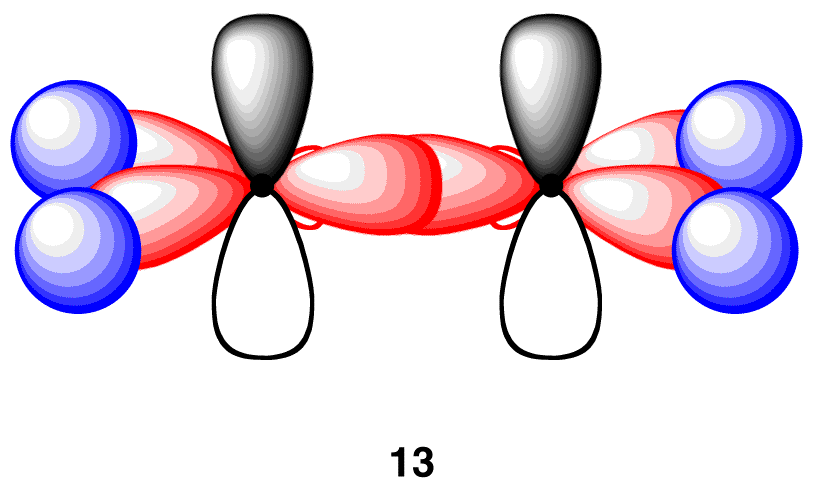
13 has the connectivity of the ethylene molecule, but neither carbon atom in 13 has an octet of valence electrons. In order to give each carbon atom in 13 an octet of electrons, overlap the two 2p orbitals laterally to create a pi bond (14).

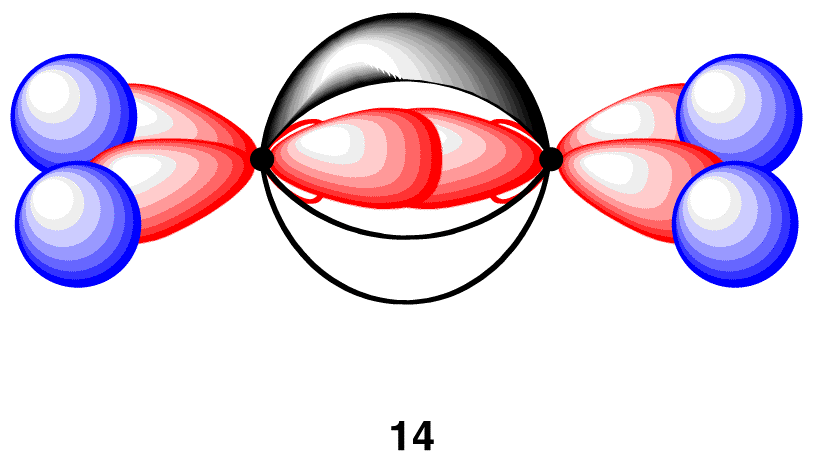
Each of the four carbon-hydrogen bonds in 14 is formed by the same overlap: sp²(C)-1s(H). Consequently, consistent with the observations, the four carbon-hydrogen bonds in 14 are identical. In addition, in 14, the carbon-carbon bond is a double bond, one sigma bond and one pi bond, which is consistent with the Lewis structure of ethylene. Finally, the geometry at each carbon atom in 14 is planar trigonal, as predicted by VSEPR theory. In summary, to explain the bonding in the ethylene molecule using the valence bond model, two modifications are necessary.

i. Use excited-state carbon atoms in bonding.

ii. Use sp²-hybridized carbon atoms in bonding.

eg. 4: acetylene

Experimentally, acetylene contains two elements, carbon and hydrogen, and the molecular formula of acetylene is C₂H₂. Like methane, ethane, and ethylene, acetylene is a covalent compound. The Lewis structure of acetylene (15) indicates that there are one carbon-carbon bond and two carbon-hydrogen bonds in the acetylene molecule.

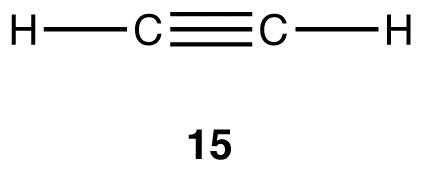
Experimentally, the two carbon-hydrogen bonds in the acetylene molecule are identical. According to VSEPR theory, the geometry at each carbon atom in the acetylene molecule is linear (15).

Each carbon atom in the acetylene molecule forms four bonds, implying that the acetylene molecule can not be constructed directly from two ground-state carbon atoms, for, as explained earlier, a ground-state carbon atom can form a maximum of only two bonds; only two excited-state carbon atoms can lead to an acetylene molecule. The coordination number of each carbon atom in the acetylene molecule is two, not four as is the case with the carbon atoms in methane and ethane molecules, nor three as is the case with the carbon atoms in the ethylene molecule, suggesting that the carbon atoms in the acetylene molecule could not possibly be sp³– nor sp²– hybridized.

Imagine mixing the 2s orbital and one of the three 2p orbitals in an excited-state carbon atom thoroughly in an excited-state carbon atom thoroughly to give a homogeneous mixture and, then, dividing the mixture into two new, identical orbitals, which are hybridized, specifically, sp-hybridized, orbitals. Since the two sp-hybridized orbitals are created by mixing one 2s orbital and one 2p orbital, the energy of an sp-hybridized orbital falls exactly halfway between those of a 2s orbital and a 2p orbital. The two atomic orbitals used in hybridization had a total of two electrons, which are to be distributed in the two sp-hybridized orbitals equally, following the Hund’s rule.

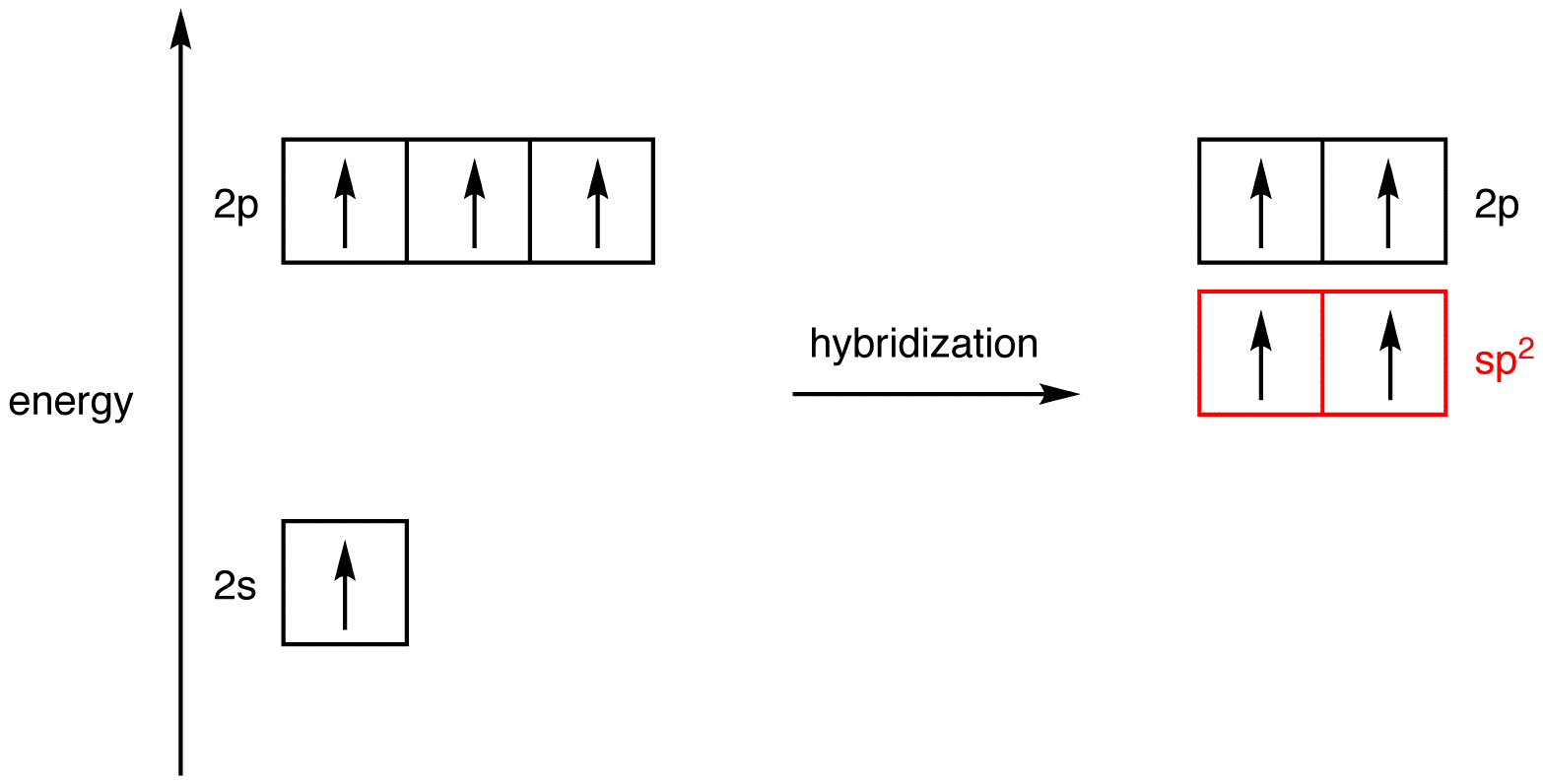
The shape of the sp-hybridized orbital is shown mathematically to be roughly the same as that of the sp³-hybridized orbital.

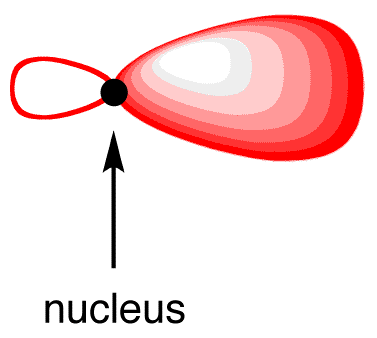
To minimize the repulsion between electrons, the two sp-hybridized orbitals arrange themselves around the carbon nucleus so that they are as far away as possible from each other, leading to their linear arrangement.

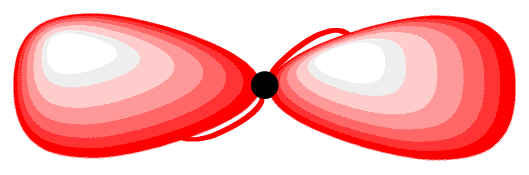
The two 2p orbitals that did not participate in hybridization, which are perpendicular to each other, each has one electron. Again, to minimize the repulsion between electrons, they position themselves so that they are as far away as possible from each sp-hybridized orbital. Each 2p orbital is as far away as possible from each sp-hybridized orbital when perpendicular to each sp-hybridized orbital (16). The carbon atom 16 is called an “sp-hybridized carbon atom.”

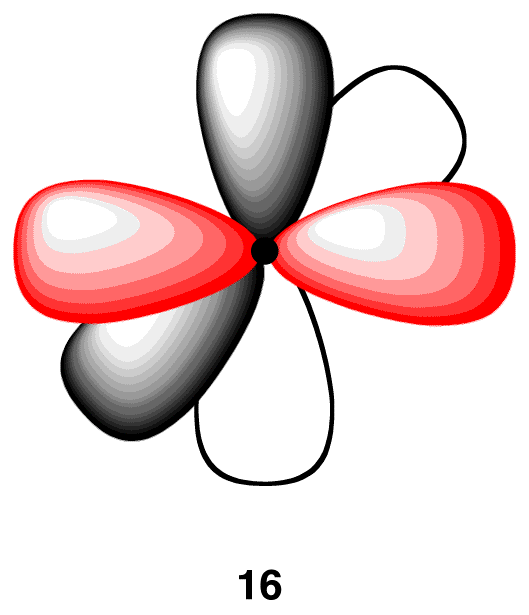
In the acetylene molecule, each carbon atom is bonded to one hydrogen atom. Thus, overlap one sp-hybridized orbital in 16 with the 1s orbital of a hydrogen atom (17).

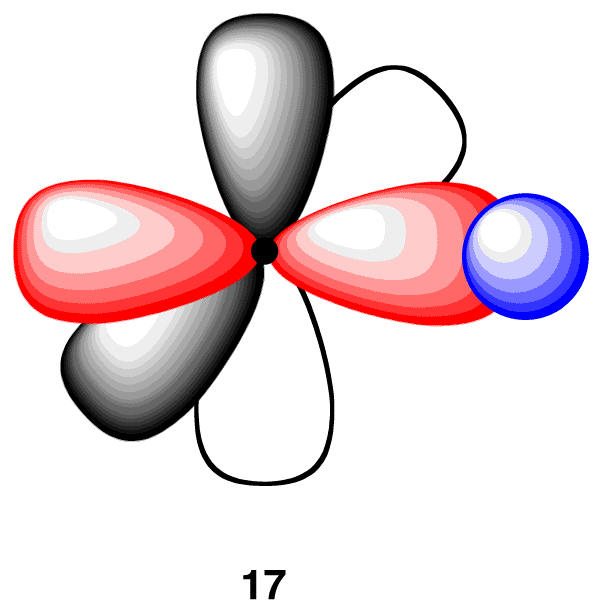
In the acetylene molecule, each carbon atom is bonded to the other carbon atom, in addition to a hydrogen atom. Thus, take two units of 17 and overlap their sp-hybridized orbitals, each having an electron, to give 18.

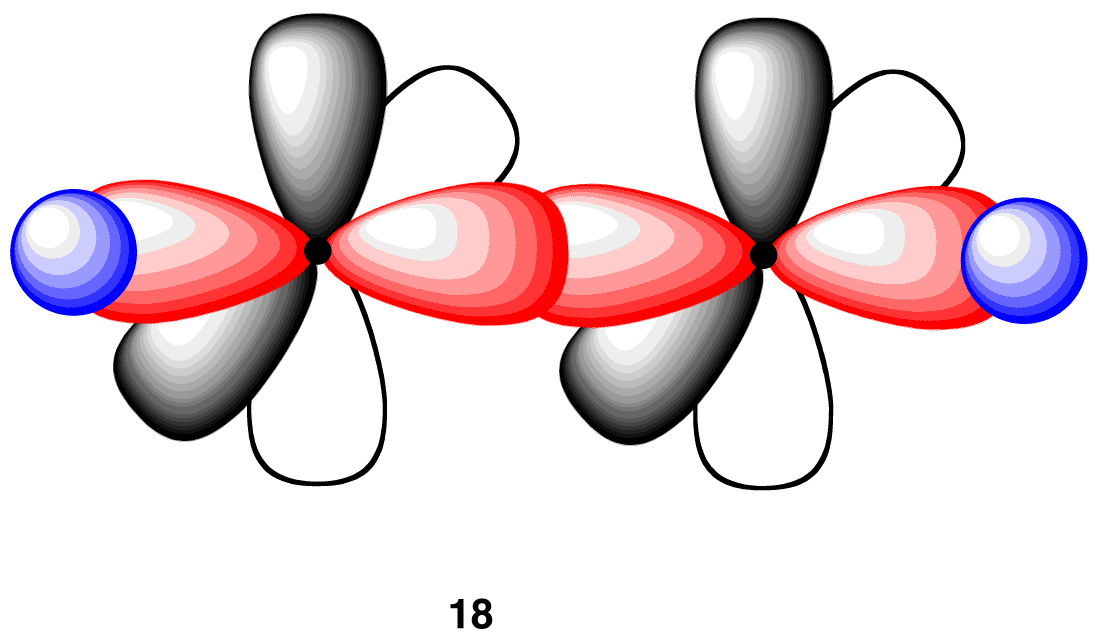
18 has the connectivity of the acetylene molecule, but, in 18, neither carbon atom has an octet of valence electrons. In order to complete the octet in each carbon atom in 18, overlap each pair of parallel 2p orbitals laterally, creating two pi bonds (19).

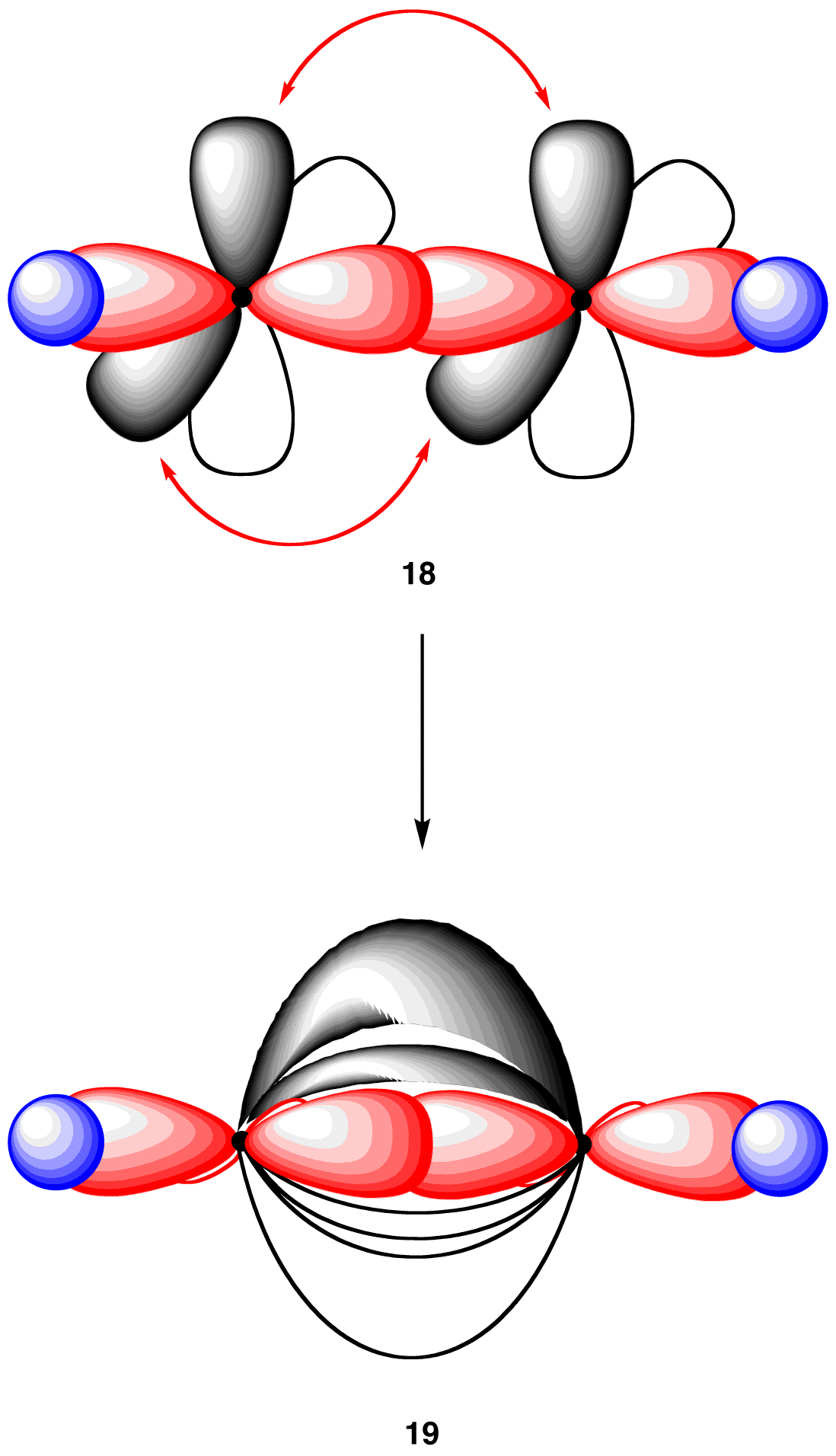
Each of the two carbon-hydrogen bonds in 19 is formed by the same overlap: sp(C)-1s(H). Consequently, consistent with observations, the two carbon-hydrogen bonds in 19 are identical. In addition, in 19, the carbon-carbon bond is a triple bond, one sigma bond and two pi bonds, which is consistent with the Lewis structure of acetylene. Finally, the geometry at each carbon atom in 19 is linear, as predicted by VSEPR theory. In summary, to explain the bonding in the acetylene molecule using the valence bond model, two modifications are necessary.

i. Use excited-state carbon atoms in bonding.

ii. Use sp-hybridized carbon atoms in bonding.

Table 1 summarizes the hybridization and geometry at the carbon atoms in methane, ethane, ethylene, and acetylene molecules.

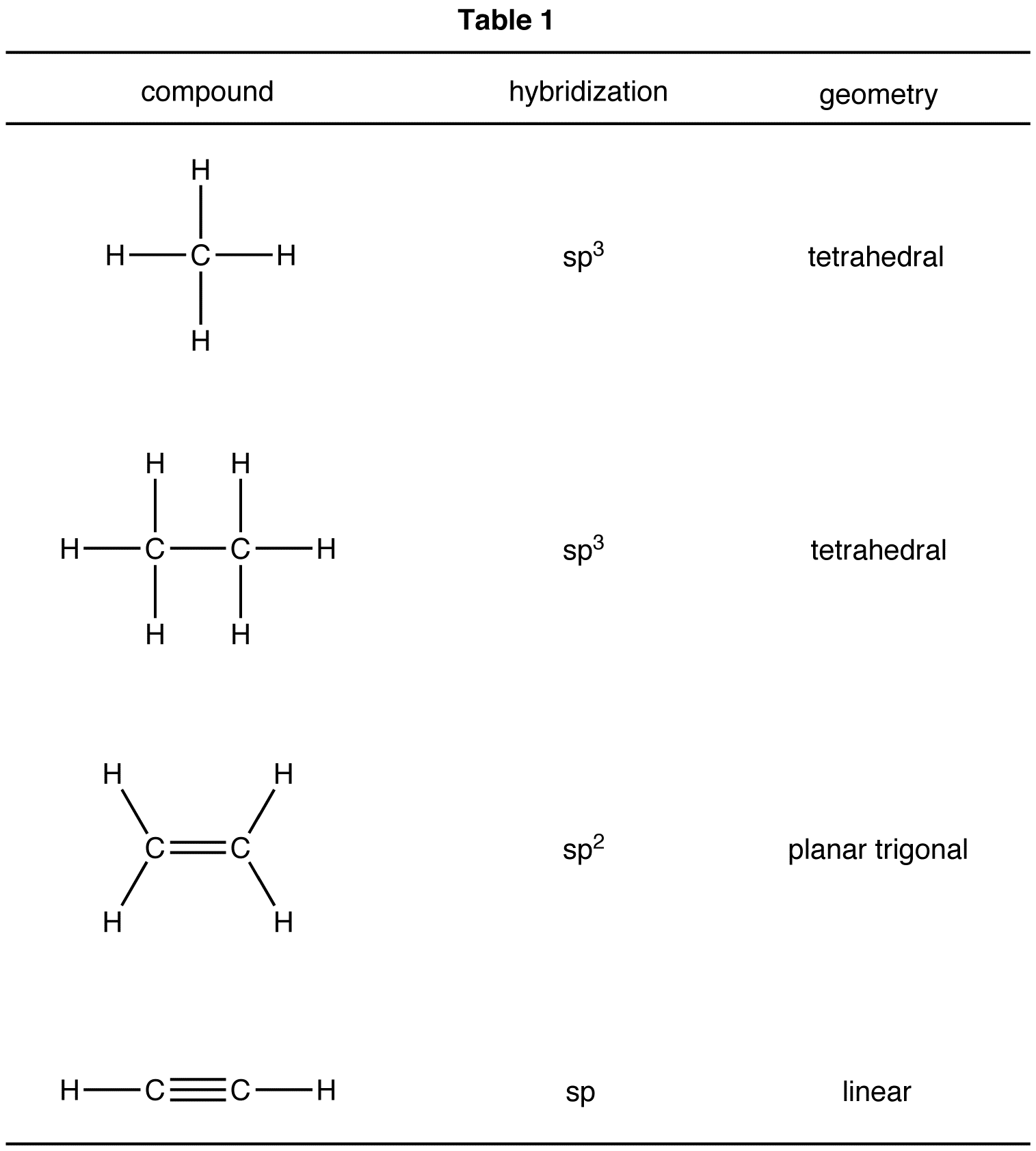
The conclusions summarized in Table 1 are general trends; they can be applied to any carbon atom in any structural formula, provided that the carbon atom possesses neither a formal charge nor unpaired valence electrons (Table 2).

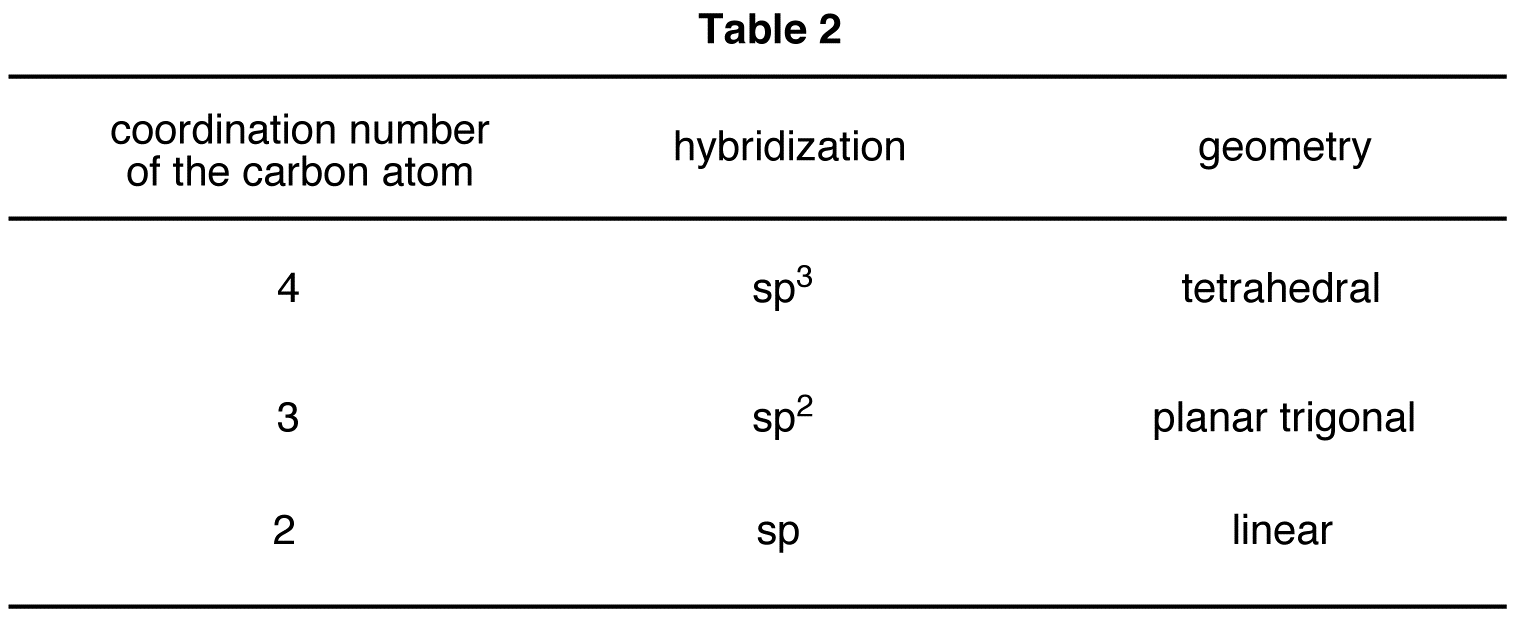
Notice the relationship between the coordination number of the carbon atom and its hybridization: The total number of orbitals participating in hybridization is equal to the coordination number of the carbon atom (Table 3).

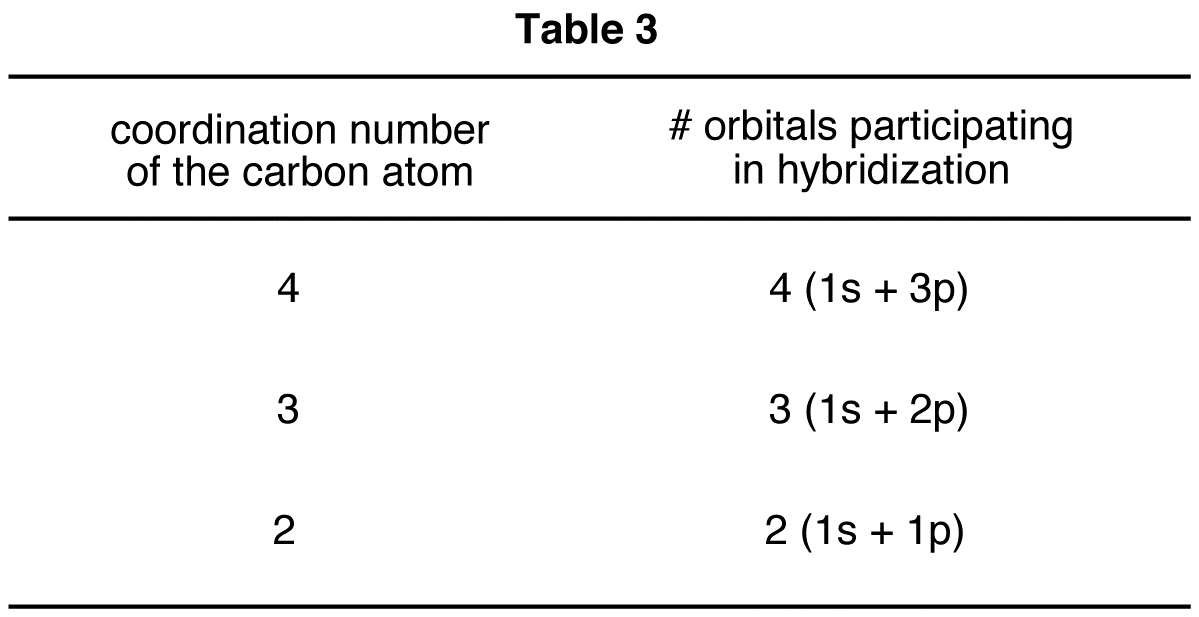
Given below are examples of applications of Table 2.

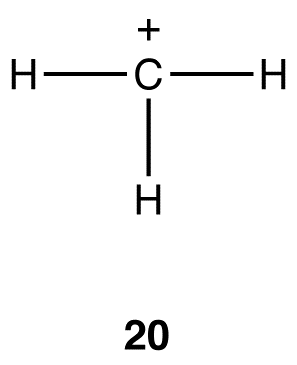
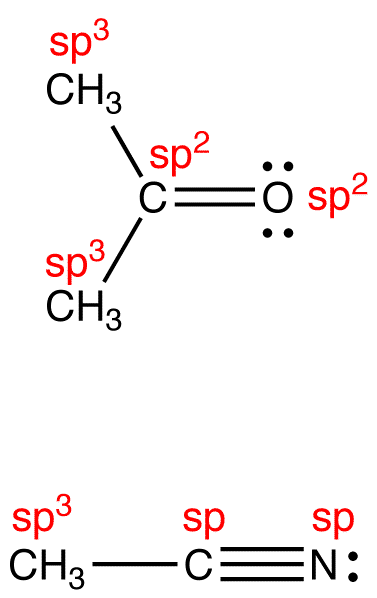
If a carbon atom bears a formal charge, the above generalizations may or may not apply. For example, in 20, the coordination number of the carbon atom is three, and, therefore, according to Table 2, the hybridization should be sp². This is consistent with experimental observations.

In 21, the coordination number at the carbon atom is three, and, therefore, the hybridization should be sp². This conclusion is not consistent with observations.

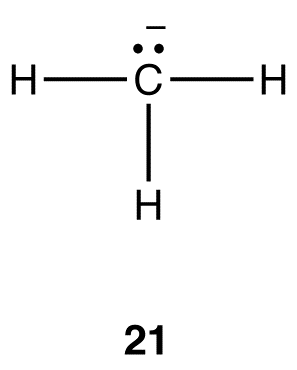
The generalizations in Table 2 can be adapted to determine the hybridization and electron-pair geometry at heteroatoms in organic molecules. For example, consider the structural formula 22.

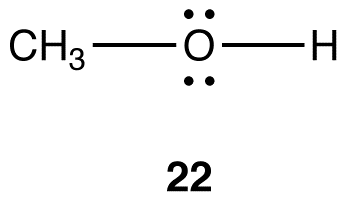
To determine the hybridization and electron-pair geometry at the oxygen atom in 22. replace the two lone pairs on the oxygen atom with phantom atoms (A).

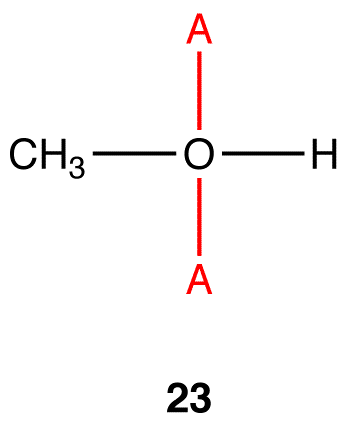
In the hypothetical molecule 23, the coordination number of the oxygen atom is four. Treat the oxygen atom in 23 as a carbon atom and apply Table 2. The hybridization at the oxygen atom in 23 is sp³, and its electron-pair geometry is tetrahedral. Thus, the hybridization at the oxygen atom in 22 is sp³ and the electron-pair geometry tetrahedral.

To determine the hybridization and electron pair geometry at any atom in an organic species, use the following formula in conjunction with Table 4.

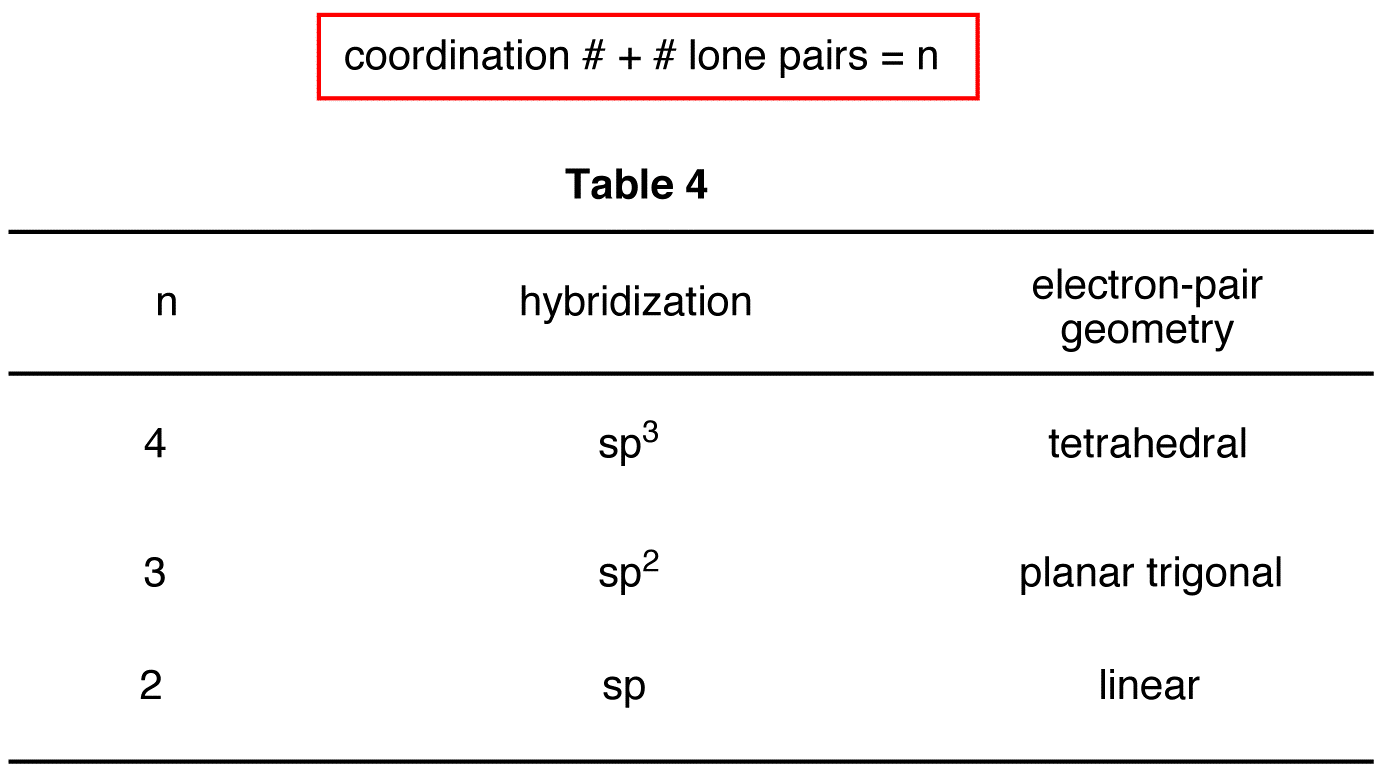
eg:

The above formula applies even if the atom under consideration bears a formal charge. For example, according to the formula, the hybridization at the carbon atom in 21 is sp³ and the electron-pair geometry tetrahedral. Experimental observations are consistent with these conclusions.

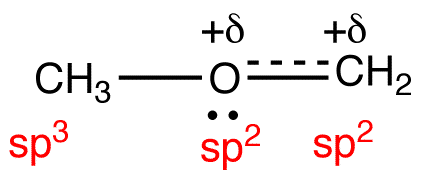
It is important to bear in mind that, if a species is resonance stabilized, the above formula is valid only to the individual resonance forms.

eg:

To determine the hybridization at the atoms in the hybrid, draw the hybrid roughly and then consider the orbitals responsible for pi bonding.

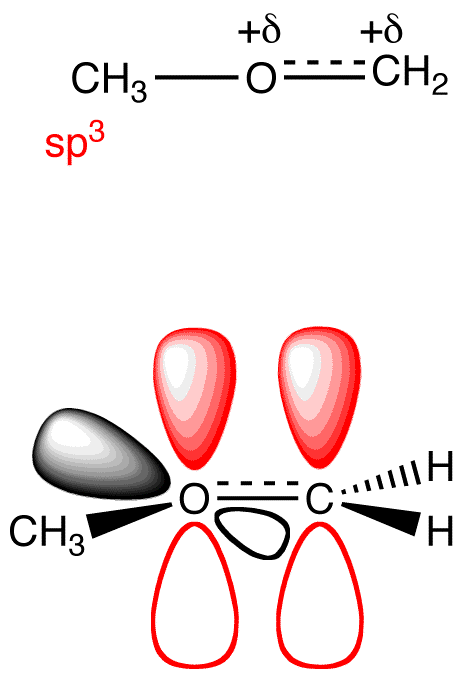
If, in the hybrid, an atom has only one p orbital overlapping laterally with other p orbitals, it is sp²-hybridized; if the number of p orbitals that overlaps with other p orbitals is two, it is sp-hybridized.