12.2: Predicting A 1H-NMR Spectrum from the Structure

Last updated
Save as PDF

Page ID: 220425

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

USEFUL READINGS

Refer to your organic chemistry lecture textbook (L.G. Wade Jr. Organic Chemistry, 6th ed.), chapter 13 (p. 559) and appendices 1A, 1B, and 1C (p. 1243). Your lab textbook also has a useful discussion in Technique 26, p. 868-899, including some useful spectra that you can compare your structures to.

REFER TO THE STRUCTURES PRESENTED ON p. 502 OF YOUR LAB TEXTBOOK

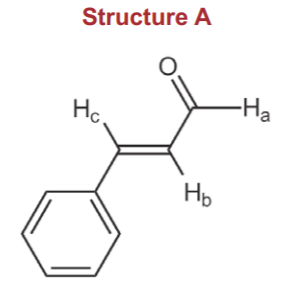
Each proton NMR signal is split into two by each nonequivalent neighboring proton. The size of the splitting (separation between the two peaks) is determined by the coupling constant J between the two neighbors. The coupling constant for two neighboring hydrogens connected through single bonds, such as H_a and H_b is J_ab, and its average value is about 6 Hz (Wade, p. 583). The coupling constant for two neighboring protons connected through a pi-bond and trans to each other, such as H_b and H_cis J_bc, and its average value is about 6 Hz (Wade, p. 583). The coupling constant for two neighboring protons connected through a pi-bond and trans to each other, such as H_b and H_cis J_bc, and its average value is about 15 Hz. Finally, when they are cis to each other (not the case in the above structure), the coupling constant average would be about 10 Hz.

At the same time that we also consider the probable chemical shift (delta) values. For an aldehyde proton such as H_a, the average chemical shift is about 9-10ppm. For vinylic protons such as H_b and H_c the average chemical shift is about 6-7 ppm. We expect H_b to be closer to 8 because of the effect of the carbonyl group, and we expect H_c to be even higher, maybe greater than 7, because of the effect of the benzene ring. Finally, the protons in the benzene ring itself have an average chemical shift of about 7-8 ppm. Thus there might be overlap between H_c and the benzene ring signals.

We typically don't try to predict the pattern of benzene ring protons because it can follow complex factors whose study is beyond the scope of this course. Therefore we will simply accept that they will appear somewhere between 7-8 ppm, but can never be sure about the degree of complexity or the shape of the multiplet.

On the following page we have the predicted proton NMR spectrum according to the above guidelines. In reality, a spectrum may or may not appear as predicted, but the predicted pattern is a starting point towards the elucidation of the structure and eventual assignment of the signals actually observed.

Predicted Spectrum (by decreasing chemical shift):

Ha: 9-10 ppm, doublet, Jab ~ 6Hz

Benzene cluster: 7-8 ppm, multiplet

Hc: 7-8 ppm, doublet, Jbc ~ 15 Hz

Hb: 6-7 ppm, doublet of doublets, Jbc ~ 15Hz, Jab ~ 6Hz

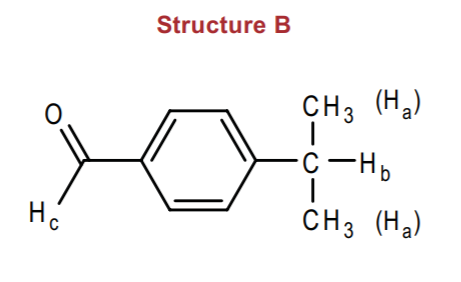
Structure B hardly requires any discussion. Once again, we simply expect a multiplet around 7-8 ppm integrating to 4 hydrogens for the benzene ring. We also expect the aldehyde proton around 9-10 ppm, expect that this time it's going to be a singlet because there are no adjacent protons.

The only other group present is the isopropyl group. Thus we expect to see the isopropyl group pattern (refer to p. 581 in the Wade textbook, 6th ed.). The methyl group doublet will probably appear between 1-2 ppm (alkane region), whereas the septet, or multiplet, will be deshielded by the benzene ring, appearing around 2-3 ppm (benzyl group region). Since the benzene ring contains an electron withdrawing group at the para-position (the aldehyde group), we expect further deshielding of the benzyl protons H_b to where they might appear closer to 3 ppm.

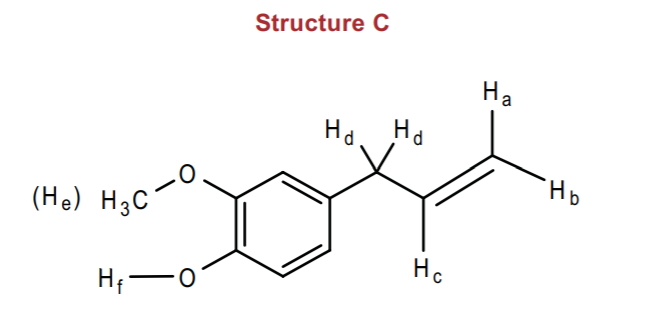
Structure C is a little more challenging. When we face this situation we try to predict the easiest patterns first. Once again, our benzene cluster will be around 7-8 ppm, expect that now we expect it to integrate to only 3 hydrogens, since the benzene ring is trisubstituted. Likewise, the methyl protons (H_e) will appear as a singlet around 3-4 ppm, which is the region assigned to ethers, and they are further deshielded by the benzene ring. H_f is the next easiest to predict. It will be a single multiplet, but hydrogen bonding signals such as alcohol protons can fluctuate in a wide range of chemical shift values, maybe between 3-6 ppm, and they could appear either as sharp or broad signals. It will obviously integrate to 1 hydrogen.

H_d protons only have one neighbor (H_c) to couple with. They are deshielded by the benzene ring and the double bond, so we expect them to appear in the allylic region, which is normally around 2 ppm (table 13.3, p. 568 in Wade) but shifted downfield to maybe 3-4 ppm. We expect it to be a doublet integrating to 2 hydrogens, with a coupling constant J_dc of about 7 Hz.

Protons, H_a, H_b, and H_c, are even more challenging. For one thing they are all vinylic protons that will appear close together, but couples to their neighbors with different coupling constants.

H_c will probably appear separate from H_a and H_b further downfield because it's closer to the benzene ring. Its signal will be split once by H_b with a coupling constant of about 10 Hz because they are cis to each other. Then it will be split twice by H_dbecause there are two of them, with coupling constant of about 7 Hz. Thus we can predict a pattern such as the following:

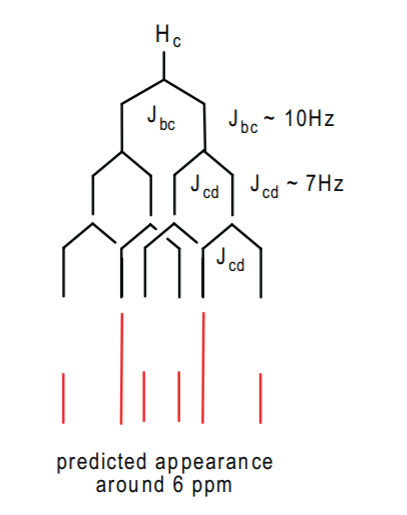
However, be warned that there might be complicating effects such as long range coupling to far away protons, and others not uncommon in this type of spectrum. This can distort the appearance of the predicted pattern. Nonetheless, H_c will appear as a complex multiplet around 6 ppm integrating to 1 hydrogen.

H_a and H_bare nonequivalent (one is cis to H_c while the other is trans) but will probably appear very close together, perhaps around 5ppm. The coupling constant between the two is very small--about 2 Hz-- since they are geminal (see p. 583 of Wade). Thus, we might predict a kind of triplet such as might be the following:

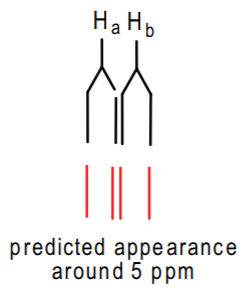
However, once again, there might be complicating effects that may distort the appearance of the predicted pattern. Nonetheless, this cluster will appear as a multiplet around 5 ppm integrating to 1 hydrogen as well.

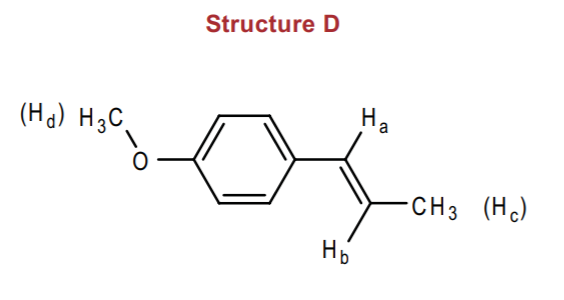
At this point you should be able to predict the appearance and chemical shifts of the methyl groups H_c and H_d, and of proton H_a, based on the previous discussions for the other molecules containing similar types of hydrogens.

H_a will probably appear as a doublet around 6-7 ppm with J_abof about 15 Hz for cis coupling and integrating to 1 hydrogen.

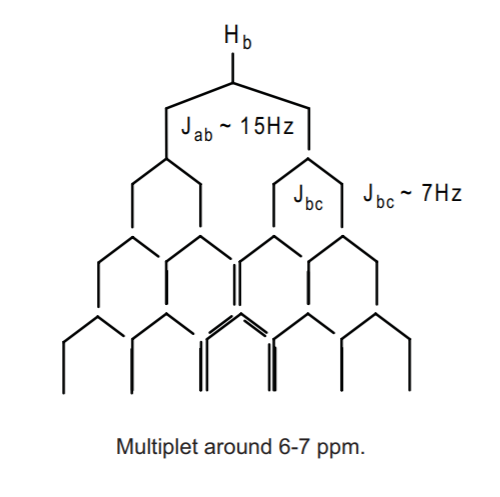
This leaves us with H_b. This will probably appear as a multiplet around 6-7 ppm (very close to H_a), split once by H_a with J_abof about 15 Hz, and three times by H_cwith J_bc of about 7 Hz. Needless to say, it will probably the most complex multiplet in the spectrum (along with the benzene ring), very close to H_aand integrating to 1 hydrogen. The tree below shows the predicted pattern, but again, we expect that the actual appearance could be distorted due to additional effects.

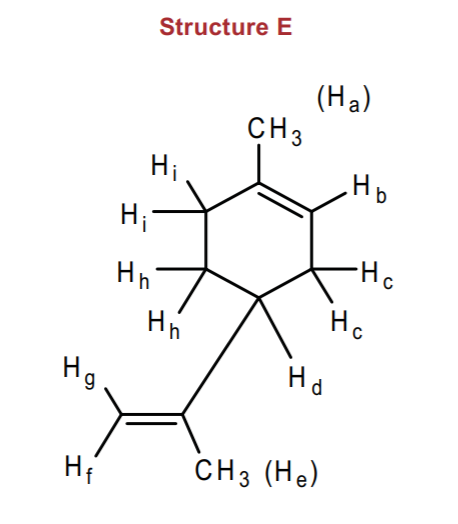
Let's consider first of all that we have several sets of allylic protons here, namely H_a, H_c,H_e, and H_i. All of these protons will probably appear close together in the allylic region, 2-3 ppm. However, the methyl groups H_a and H_e should stand out as singlets, since technically they don't have neighboring protons on adjacent carbons to couple to. HOwever, they could exhibit long range coupling to far away protons and show some fine splitting. H

Protons H_d and H_h might also appear close together and could overlap with the allylic protons, creating a highly complex multiplet. However, the methyl groups should be highly visible and should integrate to a total of 6 hydrogens. Likewise, the integral for the complex multiplet will indicate how many hydrogens it represents. Beyond these remarks we cannot say much more about the pattern of all these protons.

Next we have the vinylic protons, whose typical range is between 5-7 ppm (table 13-3 ,p. 568, Wade). First we look at the geminal protons H_f and H_g. They are nonequivalent, since one is cis and the other trans to the methyl group. They should be singlets, although probably close together, integrating to 1 hydrogen each.

Finally, proton H_b will also appear in the vinylic region, but it will be coupled to protons H_c and possibly long range coupled to other allylic prtons, creating a multiplet which also integrates to 1 hydrogen.