1.3: Diels-Alder_Reactions

Appendix 1: Diels-Alder Reactions

Mircea D. Gheorghiu

Background information

One of the most efficient methods (high yield, controlled stereochemistry, diverse functionality) to construct rings from smaller fragments is via cycloaddition reactions. The reverse reaction, namely splitting of a ring into smaller fragments is termed a cycloreversion reaction is also an important synthetic tool. (For example, in the present experiment it is the cracking of cyclopentadiene dimer to cyclopentadiene monomer.) The construction of six-membered rings built from a fragment of four atoms linked together by two conjugated double bonds (a diene) and a fragment containing two atoms linked by a double bond or triple bond (a dienophile) is known as the Diels-Alder² (D-A) reaction. It is often shorthanded as a [4+2]-\(\pi\)-electron cycloaddition. During the retro-D-A, a six-membered ring is split into a diene (often an aromatic compound) and a homonuclear (alkene, alkyne) or heteronuclear (CO) \(\pi\) bond.

The simplest example of a D-A reaction is the reaction between butadiene and ethylene to form cyclohexene. Both the diene and the dienophile display a very low reactivity. Please note the very sluggish reaction conditions: high pressure and an unusual high butadiene: ethylene molar ratio (Swiss patent, Chem. Abstract 89, 59709).

Nevertheless, a dienophile substituted with electron withdrawing group(s) and/or a diene substituted with electron donor group(s) reacts at lower temperature at atmospheric pressure resulting in cyclohexene derivatives in medium to very high yield. An alternative version is the inverse electron demand D-A reaction in which an electron-rich alkene reacts with an electron-poor diene.

The diene must be able to assume s-cis conformation. If the conjugated double bonds are rigidly fixed in the s-trans configuration, the respective diene does not undergo D-A reaction.

Larger rate acceleration (shorter reaction time at room or lower temperature, often with an increase in the regioselectivity) can be achieved using Lewis acid catalysts like AlCl₃, Et₂AlCl, BF₃, B(OAc)₃, ZnCl₂, SnCl₄ and TiCl₄. Because the Lewis acid coordinates at the Lewis base side of the dienophile, for example, at the carbonyl oxygen of methacrolein, it makes the CO group even more electron-withdrawing and, therefore, more reactive. The crystalline phase (X-ray, see figure below) and in solution structure (Nuclear Overhauser Effect) of the methacrolein boron trifluoride both display an s-trans frame of the \(\alpha , \beta\)-enal and the Lewis acid coordinated syn to the lone pair to the formyl proton.³

Stereochemistry of the D-A reaction.

1. Regioselectivity.
2. Stereoselectivity:
   1. Diastereoselective (endo, exo).
   2. Enantioselective (R, S).

1. Unsymmetrical dienes like piperylene react with methyl acrylate to yield two isomeric adducts (two regioisomers) that differ only by the relative orientation of the two substituents, methyl and carbomethoxy, respectively.

2a. In the absence of a catalyst, the endo product is preferentially formed (Alder endo rule). Cycloaddition of methacrolein to cyclopentadiene (see Table 1) yields a mixture of exo-CHO-3 and endo-CHO-3 diastereoisomers in a ratio that is dramatically dependent on reaction conditions. For example, at a relatively high temperature and longer reaction time the aldehyde group shows a preference for the endo position, (see entry 1-3). At a lower temperature and in the presence of a Lewis catalyst (see entry 4) the exo diastereoisomer is preponderantly formed. For example, cyclopentadiene, the diene employed in the present experiment, has a limited shelf lifetime at room temperature (8% is converted into its dimer in 4 h and 50% in 24 h) because it reacts with itself to form the endo diastereoisomer:

2b. D-A reactions make simultaneously two carbon-carbon bonds, and if the product lacks a plane of symmetry, they create four stereocenters in the process. Thus, a synthesis of a molecule containing several stereocenters via a Diels-Alder reaction may be particularly efficient, provided that the relative and absolute stereochemistry of the Diels-Alder reaction can be controlled. There is no general way of accomplishing this objective for all types of Diels-Alder reactions, but the catalyst developed recently (1989) in Hisashi Yamamoto’s group. (Nagoya University) provide good stereocontrol with a number of useful combinations of substrates.⁴

Table 1. Selected literature example of non-catalyzed (entries 1 –3, NA means not available), Lewis acid catalyzed (entry 4) and Lewis acid and Bronsted and Lewis acid catalyzed (entries 5-7) cycloaddition of methacrolein to cyclopentadiene.

Entry	Molar ratio Cyclopentadiene/ methacrolein	Time (h)	solvent	Temperature (C)	catalyst	Exo- CHO-3 /endo- CHO-3	Yield %	ee% (absolute config.)	Lit .
1	1:0.8	2-3	-	100	-	Mostly endo	74	-	5
2a 2b	1 : 1.19 1 : 0.8	11 10	- -	150 170	- -	Mostly endo	84 7(!)	-	6
3a 3b	NA 1 : 0.5	NA 10	NA -	NA 120	NA -	70:30 58:42	NA 74	NA -	7 8
4	1 : 0.8	?	toluene	-50	AlCl3	94:6	78	-	9
5	1 : 0.88	3	toluene	-78	Chiral* ROAlCl2	98:2	69	72	10
6	4 : 1	1.5	CH2Cl2	-78	(RO)4B**	>99:1	99	99 (R)	11
7	3 : 1	3	CH2Cl2	-78	(Acyloxy) borane***	90:10	85	96 (R)	12

• * From menthol and EtAlCl2
• ** R is a binaphthol derivative (for more details see the paper)
• *** The catalyst is the one prepared in the present experiment. The catalyst derived from natural tartaric acid yield the R isomer.

An Electronic Insight into Diels-Alder Reactions

The regio- and stereoselectivities of Diels-Alder cycloaddition are easily rationalized by examining only the frontier molecular orbitals (F.M.O.)¹³ of diene and dienophiles. Frontier orbitals are the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). Woodward and Hoffmann¹⁴ pointed out in 1965 that if the cycloaddition is concerted, during the D.-A. reaction the HOMO of the diene interacts in phase (constructive overlap) with LUMO of the dienophile:

Figure \(\PageIndex{1}\): In phase interaction of HOMO of butadiene with LUMO of ethylene.

Based on pertubation theory, Klopman¹⁵ and Salem¹⁶ have derived an expression for energy gain when the orbitals of one reactant interact with those of another. There are three terms that contribute to energy changes: the first is a closed shell repulsion (occupied orbitals of diene repel the occupied orbitals of dienophile), the second term is Coulombic repulsion and attraction (important for ionic reactions) and the third is the interaction of all filled orbitals with all the unfilled of correct symmetry (especially the HOMO of diene interacting with the LUMO of dienepholie that makes the largest contribution to equation 1). For a cycloaddition reaction the third term is defined as:

\[\Delta E = \sum^{occ.}_r \sum^{unocc.}_s - \sum^{unocc.}_s \sum^{occ.}_r \frac{2(\sum_{ab} c_{ra} c_{sb} \beta_{ab})^2}{E_r - E_s} \label{one}\]

where: \(c_{ra}\) is the coefficient of atomic orbital a in molecular orbital r, where r refers to molecular orbitals of one molecule and s refers to those on the other.

\(E_r\) is the energy of molecular orbital r.

\(\beta_{ab}\) is the resonance integral; it is assumed to be proportional with the overlap integral S.

2 is the occupancy number (interaction involves two electrons).

Figure \(\PageIndex{2}\): Orbitals interaction in a Diels-Alder reactions.

According to F.M.O. the reactivity is correlated with the properties of highest filled and lowest vacant orbitals of the reacting molecules. The interaction energy described in Equation \ref{one} now is simplified to Equation \ref{two}.

\[\Delta E = \frac{2(c^{diene}_{HOMO1} c^{dienophile}_{LUMO1} \beta_{11} + c^{diene}_{HOMO4} c^{dienophile}_{LUMO2} \beta_{24})^2}{E^{diene}_{HOMO} - E^{dienophile}_{LUMO}}
+
\frac{2(c^{dienophile}_{HOMO1} c^{diene}_{LUMO1} \beta_{11} + c^{dienophile}_{HOMO2} c^{diene}_{LUMO4} \beta_{24})^2}{E^{dienophile}_{HOMO} - E^{diene}_{LUMO}} \label{two}\]

In practice it was noted that for numerous diene-dieniophile \(E^{diene}_{HOMO} - E^{dienophile}_{LUMO} \gg E^{dienophile}_{HOMO} - E^{diene}_{LUMO}\), therefore \(\Delta E\) becomes:

\[\Delta E = \frac{2(c^{diene}_{HOMO1} c^{dienophile}_{LUMO1} \beta_{11} + c^{diene}_{HOMO4} c^{dienophile}_{LUMO2} \beta_{24})^2}{E^{diene}_{HOMO} - E^{dienophile}_{LUMO}} \label{three}\]

Thus, the larger are the coefficients and the smaller is the HOMO-LUMO energy gap, the lower is the activation energy for the respective D.-A. reaction.

Figure \(\PageIndex{3}\): F.M.O. interaction in a Diels-Alder reactions.

Substituents effect.

Why an electron-releasing group (ERG) on the butadiene skeleton and electron withdrawing-group(s) (EWG) on ethylene make the D.-A. reaction efficient and rapid?

ERG are “pushing” up the diene’s HOMO (see Fig. A5). EWG are “pushing” down the dienophile’s LUMO (see Fig. A6). Because the energy gap is becoming smaller, \(\Delta\)E is becoming larger (Equation \ref{three}). The consequence of this effect is a dramatic increase in the rate of the cycloaddition.

Figure \(\PageIndex{4}\): Substituents effect on the HOMO-LUMO gap.

Figure \(\PageIndex{5}\): Calculated (PM3-ProSpartan) HOMO energy (in eV) for some 1-substituted butadiene. The magnitude of the coefficients in the HOMO wave function at the terminal carbons is also provided. Circles with different colors means that the coefficient are of opposite signs.

Figure \(\PageIndex{6}\): Calculated (PM3-ProSpartan) LUMO energy (in eV) for some substituted Ethylene. The magnitude of the coefficients in the LUMO wave function is also provided. Circles with different colors mean that the coefficients are of opposite signs.

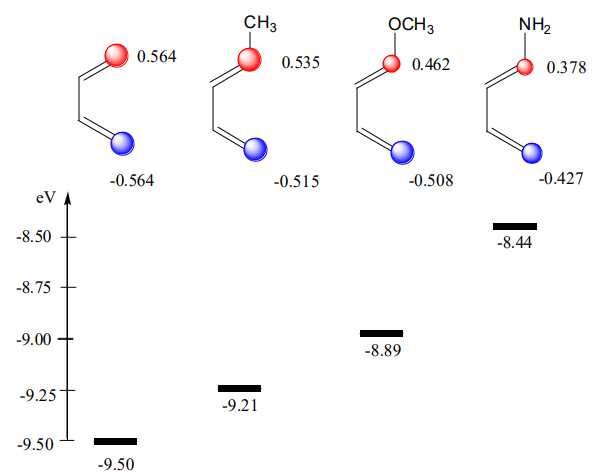
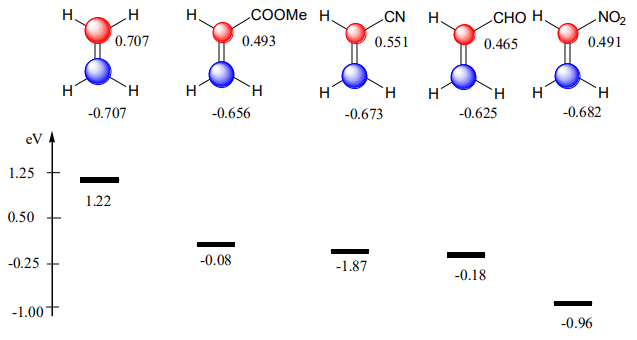
Regioselectivity.

An acceptable explanation for regioselectivity can be provided by examining the F.O. of a dienophile and diene. If the reaction is uncatalyzed and there is a lack of strong solvent effect, a key factor in orienting the direction of the cycloaddition is the size of the coefficient on the individual atoms that are forming the new bonds. The new bonds are formed preferentially when “large-large” and “small-small” (Houk rule¹⁷) overlap:

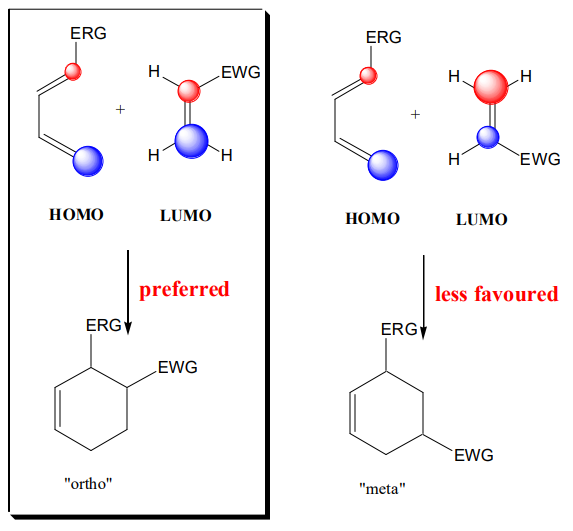
Diastereoselectivity

Endo addition is favored as a result of secondary interaction(s) (colored in blue) among the F.M.O. of diene at C₂, C₃ and dienophile at C₃. Secondary interactions will lower the height of the transition state. However, the endo diastereoisomer is less stable (because of steric repulsions) thermodynamically than the exo isomer. Although the exo isomer requires higher energy of activation, it is more stable thermodynamically. The endo isomer is said to be formed under kinetic control. The exo isomer is formed under thermodynamic control.

Lewis acid catalysis

Non-chiral catalysts.¹⁸

As result of complexation of the Lewis acid with a carbonyl group a large increase in the effective electronegativity of the substituent with a lowering of the dienophile LUMO occurs. This effect contributes to reducing the energy gap in Equation \ref{three} and hence an increase in the rate of cycloaddition. For example, in the cycloaddition of isoprene to acrylonitrile¹⁹, AlCl3 produces an acceleration of 10⁵ (!) at 20 ^oC. Additionally, note the increase in the regioselectivity.

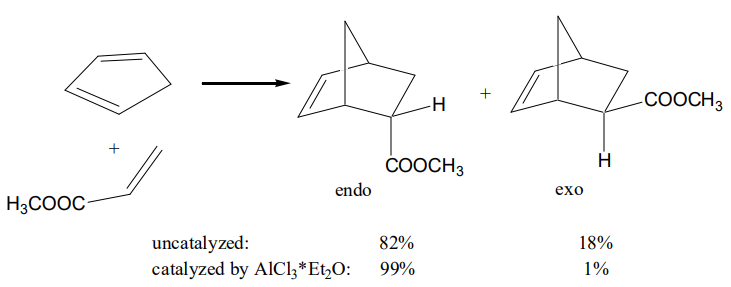
Also, the stereoselectivity, exo:endo ratios, increases if a Lewis catalyst is employed. For example, the uncatalyzed cycloaddition of cyclopentadiene to methyl acrylate yields a mixture of endo:exo diastereoisomer with a ratio of 82:12; the catalyzed cycloaddition in the presence of AlCl₃*Et₂O gives a 99:1 mixture of endo:exo isomers.²⁰

Chiral Lewis acid catalysts

In addition to the kinetic effect (low reaction temperature) that is described above, a chiral Lewis catalyst induces enantioselectivity that could reach >99% ee. The chiral tether could bring the aromatic ring only in one out of the two relevant conformation: either above the re or si face of the double bond.

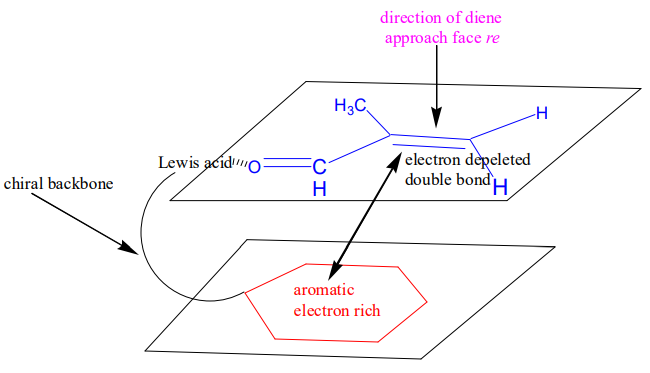
Attractive intramolecular interactions²¹ in the transition state among the electron depleted double bond (acceptor) and the electron rich aromatic ring (donor) will consolidate the conformation. The electron deprivation of CC bond is the effect of the conjugation with CO bond, which is further augmented by Lewis acid coordination to the oxygen.

Footnotes

2. Otto Diels and his student Kurt Alder received the Nobel Prize in 1950 “for their discovery and development of the diene synthesis.” The first paper, in a series that linked forever their names, is: Diels, O.; Alder, K. Ann. 1928, 460, 98.
3. Corey, E. J.; Loh, T.-P.; Sarshar, S.; Azimioara, M. Tetrahedron Letters 1992, 33, 6945.
4. For a comprehensive review of the effective catalysts inducing ee in the range of 87-99% in the cycloaddition of cyclopentadiene to methacrolein see: Corey, E. J.; Guzman-Perez, A. Angew. Chem. Int. Ed.. 1998, 37, 388.
5. Chemically assigned: Beckmann, S.; Bamberger, R. Liebigs Ann. Chem. 1953, 580, 198.
6. Chemically assigned: Meek, J. S.; Trapp, W. B. J. Am. Chem. Soc. 1957, 79, 3909.
7. First 1 H NMR assignment, exo CHO absorbs with 0.31 ppm downfield from endo CHO: Moen, R. V.; Makowski, H. S. Analytical Chem. 1971, 43, 1629.
8. Griesbeck, A. G. Synthesis. 1990, 144.
9. Bloch, R.; Gilbert, L. Tetrahedron 1988, 44, 2523.
10. Hashimoto, S.-I.; Komeshima, N.; Koga, K. J.C.S. Chem. Comm. 1979, 437.
11. Ishihara, K.; Kurihara, H.; Matsumoto, M.; Yamamoto, H. J. Am. Chem. Soc. 1998, 120, 6920.
12. Furuta, K.; Shimizy, S.; Miwa, Y.; Yamamoto, H. J. Org. Chem. 1989, 54, 1481.
13. Review: Fukui, K, Acc. Chem. Res. 1971, 4, 57.
14. Woodward, R. B.; Hoffmann, R. J. Am. Chem. Soc. 1965, 87, 4388; see also the review: Woodward, R. B.; Hoffmann, R. The Conservation of Orbital Symmetry, Verlag Chemie: Weinheim, 1970.
15. Klopmann, G. J. Am. Chem. Soc. 1968, 90, 223.
16. Salem, L. J. Am. Chem. Soc. 1968, 90, 543 and 553.
17. Houk, K. N. J. Am. Chem. Soc. 1973, 95, 4092.
18. For the first example of a Lewis acid catalyzed Diels-Alder reaction see: Yates, P.; Eaton, P. J. Am. Chem. Soc. 1960, 82, 4436.
19. Inukai, T.; Kojima, T. J. Org. Chem., 1966, 31, 1121.
20. Inukai, T.; Kojima, T. J. Org. Chem., 1967, 32, 869, 872.
21. Corey, I. J.; Loh, T.-P. J. Am. Chem. Soc., 1991, 113, 8966.