1: Measurements in the Laboratory (Experiment)
- Page ID
- 93982
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To use standard laboratory measurement devices to measure length, volume and mass amounts.
- To use these measurements to determine the areas of shapes and volumes
- To determine the density of water.
- To determine the density of a solid and use this to determine further quantities.
- To determine the density of aluminum (applying the technique of water displacement) and use that value to determine the thickness of a piece of aluminum foil.
Chemistry is the study of matter. Our understanding of chemical processes thus depends on our ability to acquire accurate information about matter. Often, this information is quantitative, in the form of measurements. In this lab, you will be introduced to some common measuring devices, and learn how to use them to obtain correct measurements, each with correct precision. A metric ruler will be used to measure length in centimeters (cm).
All measuring devices are subject to error, making it impossible to obtain exact measurements. Students will record all the digits of the measurement using the markings that we know exactly and one further digit that we estimate and call uncertain. The uncertain digit is our best estimate using the smallest unit of measurement given and estimating between two of these values. These digits are collectively referred to as significant figures. Note, the electronic balance is designed to register these values and the student should only record the value displayed.
When making measurements, it is important to be as accurate and precise as possible. Accuracy is a measure of how close an experimental measurement is to the true, accepted value. Precision refers to how close repeated measurements (using the same device) are to each other.
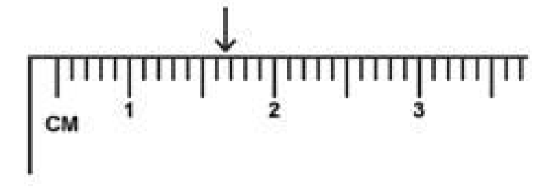
Here the “ruler” markings are every 0.1-centimeter. The correct reading is 1.67 cm. The first 2 digits 1.67 are known exactly. The last digit 1.67 is uncertain. You may have instead estimated it as 1.68 cm.
The measuring devices used in this lab may have different scale graduations than the ones shown Precision is basically how many significant figures you have in your measurement. To find the precision, you basically take the smallest unit on your measuring device, and add a decimal place (the uncertain digit).
In general, the more decimal places provided by a device, the more precise the measurement will be.
Measurements obtained in lab will often be used in subsequent calculations to obtain other values of interest. Thus, it is important to consider the number of significant figures that should be recorded for such calculated values. If multiplying or dividing measured values, the result should be reported with the lowest number of significant figures used in the calculation. If adding or subtracting measured values, the result should be reported with the lowest number of decimal places used in the calculation.
(a) A student runs 18.752 meters in 54.2 seconds. Calculate his velocity (or speed).
\[velocity = \frac{distance}{time}\]
\[= \frac{18.752 m}{ 54.2 s}\]
\[= 0.345978 m/s \text{ from calculator}\]
\[= 0.346 m/s \text{ to 3 significant figures}\]
(b) The mass of a glass is measured to be 12.456 grams. If 10.33 grams of water are added to this glass, what is the total combined mass?
\[ \text{total mass} = 12.456 g + 10.33 g\]
\[= 22.786 g \text{ from calculator}\]
\[= 22.79 g \text{ to 2 decimal places}\]
In this lab, students will also determine the density of water as well as aluminum. Volume is the amount of space occupied by matter. An extensive property is one that is dependent on the amount of matter present. Volume is an extensive property.
The volume of a liquid can be directly measured with specialized glassware, typically in units of milliliters (mL) or liters (L). In this lab, a beaker, two graduated cylinders and a burette will be used to measure liquid volumes, and their precision will be compared. Note that when measuring liquid volumes, it is important to read the graduated scale from the lowest point of the curved surface of the liquid, known as the liquid meniscus.
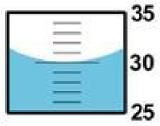
Here, the graduated cylinder markings are every 1-milliliter. When read from the lowest point of the meniscus, the correct volume reading is 30.0 mL. The first 2 digits 30.0 are known exactly. The last digit 30.0 is uncertain. Even though it is a zero, it is significant and must be recorded.
The volume of a solid must be measured indirectly based on its shape. For regularly shaped solids, such as a cube, sphere, cylinder, or cone, the volume can be calculated from its measured dimensions (length, width, height, diameter) by using an appropriate equation.
\[\text{Volume of a cube} = l \times w \times h\]
\[\text{Volume of a sphere} = \frac{4}{3} \pi r^3\]
\[\text{Volume of a cylinder} = \pi r^2 h\]
(where \(r\) = radius = 1⁄2 the diameter)
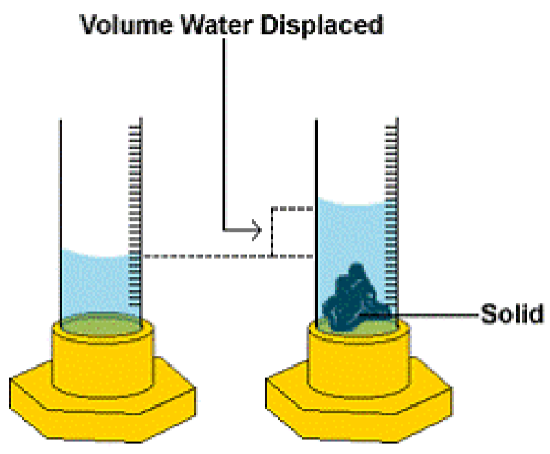
For irregularly shaped solids, the volume can be indirectly determined via the volume of water (or any other liquid) that the solid displaces when it is immersed in the water (Archimedes Principle). The units for solid volumes are typically cubic centimeters (cm3) or cubic meters (m3). Note that 1 mL = 1 cm3.
Measuring the Volume of an Irregularly Shaped Solid
The volume water displaced is equal to the difference between the final volume and the initial volume , or:
\[V=V_f -V_i\]
where the volume water displaced is equal to the volume of solid.
Density is defined as the mass per unit volume of a substance. Density is a physical property of matter. Physical properties can be measured without changing the chemical identity of the substance. Since pure substances have unique density values, measuring the density of a substance can help identify that substance. Density is also an intensive property. An intensive property is one that is independent of the amount of matter present. For example, the density of a gold coin and a gold statue are the same, even though the gold statue consists of the greater quantity of gold. Density is determined by dividing the mass of a substance by its volume:
\[density=\frac{mass}{volume}\]
Density is commonly expressed in units of g/cm3 for solids, g/mL for liquids, and g/L for gases.
Procedure
Materials and Equipment
Metric ruler, shape sheet, electronic balance, triple-beam balance, 250 mL Erlenmeyer flask, 100-mL beaker, sugar, 400-mL beaker, scoopula, burette, 10 mL and 100 mL graduated cylinders, 100 mL beaker, wooden blocks, aluminum pellets, aluminum foil, electronic balance, distilled water.
Be careful when adding the aluminum to your graduated cylinder, as the glass could break.
Personal protective equipment (PPE) needed: lab coat, safety goggles, closed-toe shoes
Part A: Measuring the Dimensions of Regular Geometric Shapes
- Borrow a ruler and “shape sheet” from the front bench. Record the ID code on your report form. Measure the dimensions of the two geometric shapes: length and width of the rectangle, and the diameter of the circle. Record these values on your lab report.
- When finished, return the ruler and sheet to the front bench.
- Use your measurements to calculate the area of each shape:
- Area of a rectangle: \(A = l \times w\)
- Area of a circle: \(A = \pi r^2\) (\(r\) = radius = 1⁄2 the diameter)
Part B: Measuring the Mass of Solids
Comparing the Precision of two types of Balances
- Obtain a 250-mL Erlenmeyer flask from your locker. Use the triple-beam balance to determine the mass of this flask.
- Use the electronic balance in the weigh room to determine the mass of the same Erlenmeyer flask. Be sure to record your measured masses on your lab report.
Weighing by Difference
- Obtain a 100-mL beaker from your locker. Use the electronic balance in the weigh room to determine the mass of this beaker.
- Add two spoonfuls of sugar to this beaker, using your scoopula. Do not do this over the balance! Determine the new combined mass of both the beaker and the sugar. Be sure to use the same electronic balance as before. When finished, dispose the used sugar in the sink.
- Use your two measurements to calculate the mass of sugar (only) by difference.
Part C: Volumes of Liquids and Solids
Volumes of Liquids
- At the front bench, you will find a burette, 10-mL graduated cylinder, 100-mL graduated cylinder and 100-mL beaker, each filled with a certain quantity of water. Measure the volume of water in each. Remember to read the volume at the bottom of the meniscus. It is useful to hold a piece of white paper behind the burette/cylinder/beaker to make it clearer.
Volume of a Regularly Shaped Solid
- Borrow a wooden block or cylinder and ruler from the front bench.
- Measure the dimensions of the block. If it is a cube or a rectangular box, measure its length, width and height. If it is a cylinder or cone, measure its height and the diameter of its circular base.
- Return the block or cylinder and ruler to the front bench when finished.
Part D: The Density of Water
- Using the electronic balance in the weigh room, determine the mass of a clean, dry, 100-mL graduated cylinder.
- Pour 40-50 mL of distilled water into the graduated cylinder and weigh. Make sure that the outside of the graduated cylinder is dry before placing it on the electronic balance.
- Measure the liquid volume in the cylinder
- Use the mass and volume to calculate the density of water.
Part E: The Density of Aluminum and the Thickness of Foil
Density of Aluminum
- Using the electronic balance in the weigh room to determine the mass of a clean, dry, small beaker.
- Obtain 20-25 aluminum pellets from the front bench. Transfer pellets to the beaker weighed in the previous step, and measure the mass of the beaker and pellets together.
- Pour 30-35 mL of water into your 100-mL graduated cylinder. Precisely measure this volume.
- Carefully add all the aluminum pellets to the water, making sure not to lose any water to splashing. Also make sure that the pellets are all completely immersed in the water. Measure the new volume of the water plus the pellets.
- When finished, retrieve and dry the aluminum pellets and return them to the front bench.
- Analysis: Use your measured mass and volume (obtained via water displacement) of the aluminum pellets to calculate the density of aluminum.
The Thickness of Aluminum Foil
- Borrow a rectangular piece of aluminum foil and ruler from the front bench. Use the ruler to measure the length and width of the piece of foil.
- Fold the foil up into a small square and measure its mass using the electronic balance in the weigh room.
- When finished, return the foil and ruler to the front bench.
- Analysis: Use these measurements along with the density of aluminum to calculate the thickness of the foil.
Lab Report: Measurements in the Laboratory
Part A: Measuring the Dimensions of Regular Geometric Shapes
Experimental Data
Shape Sheet ID Code:
|
Shape |
Dimensions |
Precision |
Measurement |
# Significant Figures |
|---|---|---|---|---|
|
Rectangle |
Length |
|||
|
Width |
||||
|
Circle |
Diameter |
Data Analysis
- Perform the conversions indicated. Show your work, and report your answers in scientific notation.
- Convert the measured rectangle length to hm.
- Convert the measured circle diameter to nm.
- Calculate the areas of your rectangle and circle in cm2. Show your work, and report your answers to the correct number of significant figures.
- Area of rectangle
- Area of circle
Part B: Measuring the Mass of Solids
Experimental Data
Table 1: Mass of an Erlenmeyer Flask
|
Measuring Device |
Mass Measurement |
# Significant Figures |
|---|---|---|
|
Triple-Beam Balance |
||
|
Electronic Balance |
Table 2: Weighing by Difference
|
Mass Measurement |
# Significant Figures |
|
|---|---|---|
|
Mass of Empty Beaker |
||
|
Mass of Beaker + Sugar |
Data Analysis
- Compare your mass values obtained for the Erlenmeyer flask (in Table 1). Which balance, triple- beam or electronic, provides the more precise measurement? Explain.
- Consider the data you obtained in Table 2.
- Calculate the mass of sugar weighed out. Show your work.
- Circle one: When performing the above calculation, significant figures / decimal places are the primary consideration.
- Perform the conversions indicated below. Show your work, and report your answers in scientific notation.
- Convert the mass of the sugar weighed out to dg.
- Convert the mass of sugar weighed out to lbs.
Part C: The Volumes of Liquids and Solids
Table 1: The Volume of Liquid Water
|
Measuring Device |
Precision |
Volume Measurement |
# Significant Figures |
|---|---|---|---|
|
Burette |
|||
|
Beaker |
|||
|
100-mL Graduated Cylinder |
|||
|
10-mL Graduated Cylinder |
Table 2: The Volume of a Regular Solid, shaped as a
|
Dimensions Measured |
Measurement |
# Significant Figures |
|---|---|---|
Data Analysis
Use your measured block dimensions (in Table 2) to calculate the block volume, in cm3. Show your work, and report your answer to the correct number of significant figures.
Part D: The Density of Water
Table 1: The Density of Water
|
Mass of Empty, Dry Graduated Cylinder |
|
|---|---|
|
Mass of Graduated Cylinder + Water |
|
|
Mass of Distilled Water |
|
|
Volume of the Distilled Water in Graduated Cylinder |
Calculate the density of water, in g/mL. Show your work, and report your answer to the correct number of significant figures.
Part E: The Density of Aluminum and the Thickness of Foil
Experimental Data
Table 1: The Density of Aluminum
|
Mass of empty beaker |
|
|---|---|
|
Mass of beaker and pellets |
|
|
Mass of pellets |
|
|
Initial volume of water in cylinder |
|
|
Final volume of water and pellets |
|
|
Volume of pellets |
Table 2: The Thickness of Aluminum Foil
|
Mass of foil |
|
|---|---|
|
Length of foil |
|
|
Width of foil |
Data Analysis
- Use your measured mass and volume of the aluminum pellets (in Table 1) to calculate the density of aluminum, in g/cm3. Show your work, and report your answer to the correct number of significant figures.
- Use your measurements for the aluminum foil (in Table 2) along with the true density of aluminum (\(_D_{Al}\) = 2.70 g/cm3) to calculate the foil thickness, in cm. Consider the foil to be a very flat rectangular box, where Volume of foil = V = length \(\times\) width\(\times\) height (thickness). Show your work, and report your answer in scientific notation.