5: pH Measurement and Its Applications (Experiment)
- Page ID
- 94006
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To measure the pH of various solutions using pH indicators and meter.
- To determine the value of \(K_{a}\) for an unknown acid.
- To perform a pH titration (OPTIONAL, if time permits)
- To create and study the properties of buffer solutions.
Part A: Using Indicators to Measure pH
In this part of the experiment you will use five indicators to determine the pH of four solutions to within one pH unit. An acid-base indicator is a chemical species that changes color at a specific pH as the pH (acidity) of the solution is varied. Acid-base indicators are themselves weak acids where the color of the aqueous acid is different than the color of the corresponding conjugate base. We can represent the dissociation of an acid-base indicator in an aqueous solution with the following equation.
\[\underbrace{\ce{HIn (aq)}}_{\text{yellow}}+\ce{H2O (l) <=> } \underbrace{\ce{In^{-} (aq)}}_{\text{blue}} + \ce{H3O^{+} (aq) } \label{1}\]
In this hypothetical example \(\ce{In}\) stands for the indicator. As you can see from Equation \ref{1}, the protonated form of the acid-base indicator, \(\ce{HIn}\) (aq), will be one color (yellow in this example) and the deprotonated form, \(\ce{In^{-}}\) (aq), will be another color (blue in this example). The equilibrium-constant expression for Equation \ref{1} is:
\[K_{ai} =\dfrac{[\ce{H3O^{+}}][\ce{In^{-}}]}{[\ce{HIn}]} \label{2}\]
This equation can also be written as:
\[ \dfrac{[\ce{In^{-}}]}{[\ce{HIn}]}= \dfrac{K_{ai}}{ [\ce{H3O^{+}}]} \label{3}\]
Generally only one or two drops of indicator are added to the solution of interest and therefore the amount of \(\ce{H3O^{+}}\) due to the indicator itself can be considered negligible. The total amount of \(\ce{H3O^{+}}\) in the solution is therefore controlled by the concentrations of the other acids and/or bases present in the solution. Note that when \([\ce{H3O^{+}}] >> K_{ai}\), \([\ce{HIn}] >> [\ce{In^{–}}]\) (the equilibrium will be shifted to the left in accord with Le Chatelier's principle) and the color of the solution will be essentially the same as color I. Similarly, when \([\ce{H3O^{+}}] << K_{ai}, [\ce{HIn}] << [\ce{In^{–}}]\) (the equilibrium will be shifted to the right) and the color of the solution will be essentially the same as color II.
As an example consider an acidic solution containing the indicator \(\ce{HIn}\) where \([\ce{H3O^{+}}] >> K_{ai}\), and therefore, \([\ce{HIn}] >> [\ce{In^{–}}]\). Under these conditions the solution will be yellow. Suppose we add base to the solution resulting in a decrease of \([\ce{H3O^{+}}]\). As \([\ce{H3O^{+}}]\) decreases the equilibrium indicated by Equation \ref{1} will shift to the right and \([\ce{HIn}]\) will decrease while \([\ce{In^{–}}]\) increases. When \([\ce{In^{–}}]\) becomes significant compared to \([\ce{HIn}]\) the color of the solution will begin to change. Eventually as \([\ce{H3O^{+}}]\) decreases still further we will have, \([\ce{H3O^{+}}] << K_{ai}\), and the color of the solution will have turned to blue. In other words the solution will change color when \([\ce{HIn}] ≈ [\ce{In^{–}}]\), and so \(K_{ai} = [\ce{H3O^{+}}]\), or \(pK_{ai} = pH\). In general we can say that an acid-base indicator changes color at a pH determined by the value of \(K_{ai}\) or pKai for that particular indicator.
The five indicators you will use in this experiment, their color transitions, and their respective values of \(\text{p}K_{ai}\) are given in Table 1.
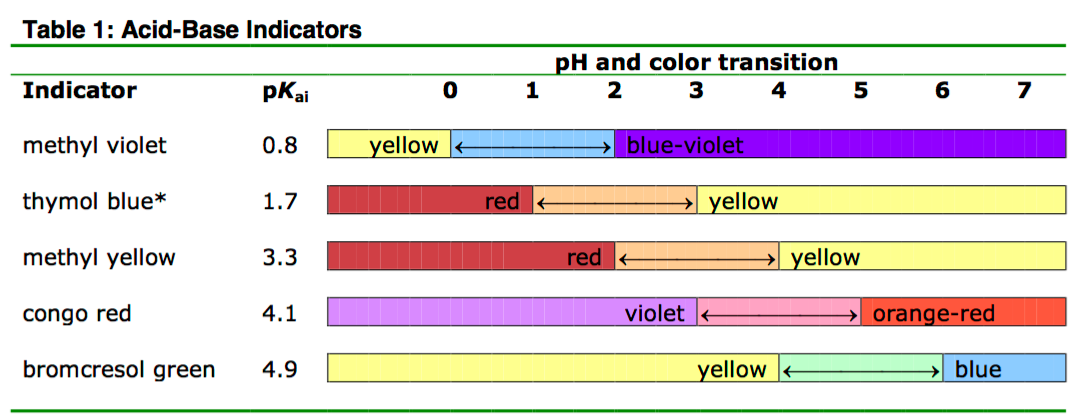
The actual colors in solution vary somewhat from those shown here depending on the concentration. *Thymol blue is a polyprotic acid with two pKa values. The second pKa is around 8.8. Adding too much NaOH, to a pH beyond its second pKa results in a colorless solution.
We can use the values in Table 1 to determine the approximate pH of a solution. For example, suppose we have a solution in which methyl violet is violet. This tells us that the pH of our unknown solution is greater than or equal to 2 because methyl violet turns violet at pH values of 2 or greater. Now suppose we add some congo red to a fresh sample of our solution and find that the color is violet. This tells us that the pH of our solution is less than or equal to 3 because congo red turns violet at pH values of 3 or less. From these two tests we know that the pH range our solution is between 2 and 3. Thus, we have determined the pH of our solution to within one pH unit. Proceeding in a similar manner, you will use the acid-base indicators in Table 1 to determine the pH range of four solutions to within one pH unit.
Part B: Using pH Meters
In this part of the experiment you will learn to use a pH meter to measure pH. Your instructor will demonstrate how to use the pH meter appropriately at the beginning of your laboratory session.
Part C: Using pH to Determine the Value of \(K_{a}\) for Acetic acid, \(\ce{CH3COOH}\)(aq)
In this part of the experiment you will use your pH meter to measure the pH of two acetic acid solutions of known concentration. From the measured pH and concentration of a weak acid solution you can determine the value of \(K_{a}\) for the acid. The general equation for the dissociation of a weak acid, \(\ce{HA}\) (aq), in water is:
\[\ce{HA (aq) + H2O (l) <=> A(aq) + H3O^{+} (aq)} \label{4}\]
For which
\[K_{a}=\dfrac{[\ce{A}] [\ce{H3O^{+}}]}{[\ce{HA}]} \label{5}\]
When we construct an ICE table for this reaction we can see that at equilibrium
\[[\ce{A^{-}}] = [\ce{H3O^{+}}] \label{6}\]
and
\[[\ce{HA}] = [\ce{HA}]_{0} - [\ce{H3O^{+}}] \label{7}\]
where \([\ce{HA}]_{0}\) is the initial (nominal) concentration of \(\ce{HA}\) (aq) before equilibrium is established.
Using Equations \ref{6} and \ref{7} , we may express Equation \ref{5} as
\[K_{a}=\dfrac{[\ce{H3O^{+}}]^{2} }{[\ce{HA}]_{0} - [\ce{H3O^{+}}]} \label{8}\]
Because \([\ce{H3O^{+}}]\) can be determined by measuring the pH of the weak acid and \([\ce{HA}]_{0}\) is known you can determine the value of \(K_{a}\) using Equation \ref{8}.
Part D: Determining the Value of \(K_{a}\) for an Unknown Acid by Titration
Note: There are two procedures listed for this part. Please consult your instructor to see which procedure is appropriate for your lab section.
- Titration is performed without collecting pH data for a Titration curve.
- OPTIONAL procedure: Titration is performed while collecting pH data for a Titration curve.
For either procedure you will perform a titration on an unknown acid. You may assume that this acid is a weak monoprotic acid.
You will divide the solution containing this unknown acid into two equal parts. One part you will set aside and the other part will be titrated with \(\ce{NaOH}\). Upon completion of the titration, the titrated solution will contain only the conjugate base of the weak acid according to
\[\ce{HA(aq) + OH^{-} (aq) <=> A^{-}(aq) + H2O(l)} \label{9}\]
Here we are assuming Equation \ref{9} proceeds essentially to completion. This can be justified by noting that for the reaction, \(K_{c} = \frac{1}{K_{b}}\) where \(K_{b}\) relates to the reaction of the conjugate base \(\ce{A^{-}}\) with water. Since \(\ce{A^{-}}\) is known to be a weak base we know that \(K_b << 1\) and therefore \(K_c >> 1\).
Next you will equalize the volumes of the two solutions by adding water to the \(\ce{HA}\) solution. This will ensure \([\ce{A^{-}}]\) in the titrated solution is equal to \([\ce{HA}]\) in the \(\ce{HA}\) solution. You will then combine equal volumes of these two solutions in order to form a new solution. This new solution will be a buffer solution since it will contain equal amounts of \(\ce{HA}\) (aq) and \(\ce{A^{-}}\) (aq). Recall that the pH of a buffer solution is given by the Henderson-Hasselbach approximation:
\[pH=pKa+ \dfrac{\log[A^{-}]}{[HA]} \label{10}\]
Because \([\ce{HA}] = [\ce{A^{-}}]\), the pH of this buffer solution equals the value of pKa for the unknown acid. Thus we can use the measured pH of this buffer solution to determine the value of pKa for our unknown acid.
OPTIONAL
If time allows you will measure the pH as a function of the volume of \(\ce{NaOH}\) solution added in the titration. These data will be used to plot a titration curve for your unknown acid. You will then use this curve to find the midpoint of the titration. At the midpoint of the titration of a weak acid with a strong base, \(pH = pK_{a}\). Thus we can use the midpoint of the titration curve to confirm the value of pKa for the unknown acid.
Part E: Buffer Solutions
In this part of the experiment you will prepare a buffer solution with a pH specified by your instructor using appropriate portions of the \(\ce{A^{-}}\) and \(\ce{HA}\) solutions prepared in Part D.
This can be accomplished using Equation \ref{10} to determine the ratio, \(\frac{[\ce{A^{-}}]} {[\ce{HA}]}\), that will produce the specified pH of the buffer solution. You will confirm the pH of this solution using your pH meter.
Finally, you will compare the buffering capacity of the buffer you prepare with that of deionized water.
Procedure
Materials and Equipment:
You will need the following additional items for this experiment: pH meter, magnetic stirrer and stir-bar, 50-mL buret
Students must wear safety goggles and lab coats at all times.
GLOVES: Gloves are needed when handling:
- zinc sulfate
- sodium carbonate
- sodium bisulfate
- methyl yellow
- congo red
- bromocresol green
- phenolphthalein
- unknown acid
WASTE DISPOSAL: All chemicals used must go in the proper waste container for disposal.
Part A: Determination of pH using Acid-Base Indicators
- Rinse five small test tubes using deionized water (there is no need to dry these). To each of these test tubes add about 1 mL of 0.1 M \(\ce{HCl}\) (aq). (Estimate these volumes). To each of these test tubes add one of the five indicators listed in Table 1. Be sure to arrange or label your test tubes so that you know which indicator was added to which tube.
- By comparing the colors you observe in each tube you should be able to determine the pH of the 0.1 M \(\ce{HCl}\) solution to within one pH unit (see background discussion). Record your color observations and your determination of the pH range of the 0.1 M \(\ce{HCl}\) solution on your data sheet.
- Repeat the same procedure using each of the following solutions:
0.1 M sodium hydrogen phosphate, \(\ce{NaH2PO4}\) (aq)
0.1 M acetic acid, \(\ce{CH3COOH}\) (aq)
0.1 M zinc sulfate, \(\ce{ZnSO4}\) (aq)
- Record your results for each on your data sheet.
Part B: Using pH Meters
Your instructor will demonstrate the proper use of the pH meters.
- Rinse four small 100 or 150-mL beakers several times using deionized water. Do not use any soap as the residue may affect your pH measurements.
- Into each of your four clean beakers collect about 30 mL of one of the following:
0.1 M sodium chloride, \(\ce{NaCl}\) (aq)
0.1 M sodium carbonate, \(\ce{Na2CO3}\) (aq)
0.1 M sodium acetate, \(\ce{NaCH3COO}\) (aq)
0.1 M sodium hydrogen sulfate, \(\ce{NaHSO4}\) (aq)
- Use your pH meter to determine the pH of each of these four solutions. Record the results on your data sheet. Add a drop or two or bromcresol green indicator to each of these solutions. Record the color of the indicator in each solution on your data sheet.
Part C: Using pH to Determine the Value of \(K_{a}\) for Acetic Acid, \(\ce{CH3COOH}\) (aq)
- Rinse two small 100 or 150-mL beakers as before. Put 30 mL of 1.0 M acetic acid solution into the first beaker and 30 mL of 0.010 M acetic acid solution into the second.
- Use your pH meter to determine the pH of each solution. Record the results on your data sheet. You will use these values to calculate \(K_{a}\).
**Consult your instructor before starting Part D, to see if he/she wants you to follow the normal or OPTIONAL procedure.
Part D: Determining the Value of \(K_{a}\) for an Unknown Acid by Titration (Normal procedure)
- Obtain a 50-mL buret from the stockroom. A buret stand should be available in the laboratory room. Rinse your buret, small funnel, and four 150-mL beakers several times using deionized water.
- Select one of the 150-mL beakers and label it “NaOH”. Rinse this beaker once more with about 5 mL of 0.2 M \(\ce{NaOH}\). Then use it to collect about 75 mL of the 0.2 M \(\ce{NaOH}\) solution (available in the reagent fume hood).
- Rinse the 50-mL buret and funnel once with about 5 mL of 0.2 M \(\ce{NaOH}\) solution. Clamp the buret to the buret stand making sure that it is vertical. Insert your funnel into the top of the buret.
- Fill the buret with the 0.2 M \(\ce{NaOH}\) solution from your beaker to just above the 0.00-mL mark. Remove the funnel. Using a waste beaker allow the \(\ce{NaOH}\) solution to flow from the buret tip dropwise until the bottom of the meniscus of the \(\ce{NaOH}\) solution in the buret is exactly at the 0.00-mL mark when read at eye level. If you miss this mark, add some additional 0.2 M \(\ce{NaOH}\) from your beaker and try again.
- Obtain a vial containing your unknown solid acid from your instructor and record the letter and number of this unknown acid on your data sheet.
- Weighing by difference measure between 1.5 and 2.0 grams of the unknown acid into one of the clean rinsed 150-mL beakers. Record this mass on your data sheet. Label this beaker, “A- ”.
- Using your large graduated cylinder, measure out exactly 100.0 mL of deionized water. Combine this with the unknown solid acid sample in your 150-mL beaker. Stir your solution to completely dissolve the solid acid.
- Using your large graduated cylinder, measure out 50.0 mL of your unknown acid solution and transfer this to a second 150-mL beaker. Label this second beaker “HA” and set it aside for now.
- Add 2 drops of phenolphthalein indicator to the remaining 50.0-mL of unknown acid solution in the beaker labeled “A- ”.
- Titrate the solution in the beaker labeled “A- ”. until it reaches the phenolphthalein end point. The end point is near when the pink color from the phenolphthalein indicator begins to persist in solution longer before vanishing. When you notice these changes slow down your addition rate to just 2 to 3 drops per addition. When you feel you are nearing the endpoint, slow down your addition rate to just 1 drop per addition. When the pink color from the phenolphthalein indicator persists for at least 2 minutes you have reached the endpoint of your titration.
- We now need to equalize the volumes in the two beakers labeled “HA” and “A- ”. Using your large graduated cylinder measure a volume of deionized water equal to the total amount of the 0.2 M \(\ce{NaOH}\) you added during your titration and add this volume of deionized water to the contents of the beaker labeled, “HA”. Swirl gently to mix.
- Using your large graduated cylinder measure out 25-mL of the solution from the beaker labeled “HA” and transfer this volume to your fourth clean rinsed 150-mL beaker. Label this beaker, “50-50 buffer mixture.”
- Now measure out 25-mL of the solution from the beaker labeled “A- ” and combine this with the solution in your beaker labeled “50-50 buffer mixture”. Swirl gently to mix. Using your pH meter, measure the pH of this solution and record the value on your data sheet.
- The pH of the solution in your beaker labeled, “50-50 buffer mixture,” is also the pKa of your unknown acid. Do you know why? You will need to tell your instructor this value for Part E.
- Save the remaining solutions in the beakers labeled, “HA” and“A- ” and the beaker containing the remaining 0.2 M \(\ce{NaOH}\) solution for the next part of this experiment.
Part D: Determining the Value of \(K_{a}\) for an Unknown Acid by Titration (OPTIONAL procedure)
Follow the procedure below for Part D instead of the steps above if your instructor wants you to also obtain a pH titration curve
- Obtain a magnetic stirrer, magnetic stir-bar, and 50-mL buret from the stockroom. A buret stand should be available in the laboratory room.
- Rinse your buret, small funnel, and four 150-mL beakers several times using deionized water.
- Select one of the 150-mL beakers and label it “NaOH”. Rinse this beaker once more with about 5 mL of 0.2 M \(\ce{NaOH}\). Then use it to collect about 75 mL of the 0.2 M \(\ce{NaOH}\) solution.
- Rinse the 50-mL buret and funnel once with about 5 mL of 0.2 M \(\ce{NaOH}\) solution. Clamp the buret to the buret stand making sure that it is vertical. Insert your funnel into the top of the buret.
- Fill the buret with the 0.2 M \(\ce{NaOH}\) solution from your beaker to just above the 0.00-mL mark. Remove the funnel. Using a waste beaker allow the \(\ce{NaOH}\) solution to flow from the buret tip dropwise until the bottom of the meniscus of the \(\ce{NaOH}\) solution in the buret is exactly at the 0.00-mL mark when read at eye level. If you miss this mark, add some additional 0.2 M \(\ce{NaOH}\) from your beaker and try again.
- Obtain a vial containing your unknown solid acid from your instructor and record the letter and number of this unknown acid on your data sheet.
- Weighing by difference measure between 1.5 and 2.0 grams of the unknown acid into one of the clean rinsed 150-mL beakers. Record this mass on your data sheet. Label this beaker, “A- ”.
- Using your large graduated cylinder, measure out exactly 100.0 mL of deionized water. Combine this with the unknown solid acid sample in your 150-mL beaker. Stir your solution to completely dissolve the solid acid.
- Using your large graduated cylinder, measure out 50.0 mL of your unknown acid solution and transfer this to a second 150-mL beaker. Label this second beaker “HA” and set it aside for now.
- Add 2 drops of phenolphthalein indicator to the remaining 50.0-mL of unknown acid solution in the beaker labeled “A- ”.
- Put the magnetic stirrer onto your buret stand so that the buret is directly over the magnetic stirrer.
- Place the magnetic stir-bar into the solution in the beaker labeled “A- ”. and set this beaker on top of the magnetic stirrer. Plug in the magnetic stirrer and set it to the lowest setting where the solution is mixing smoothly but gently. If the magnetic stirrer also has a heater function be certain that this remains off throughout this experiment.
- Using a ring stand and your utility clamp, or the stand and clamp provided with your pH meter’s probe, set up the pH meter so that the probe is supported inside the swirling solution in your beaker, low enough down that the meter can read the pH, but high enough up so that the probe tip does not contact the rotating magnetic stir-bar, as shown in Figure 1. Set the probe off to one side of the beaker so that liquid from the buret can directly enter the beaker during the titration.

- Use the pH meter to measure the pH of the solution in the beaker labeled “A- ”. Record this value in the table on your data sheet. This pH is the “initial point” in your titration.
- Dispense approximately 0.5-mL of the 0.2 M \(\ce{NaOH}\) solution from your buret into your beaker. Reading the buret carefully, record the exact volume added on your data sheet. Use the pH meter to measure the pH of the solution following this addition. Record this value in your data table alongside the measured volume.
- Proceeding in this way, continue to add 0.2 M \(\ce{NaOH}\) to your solution in approximately 0.5-mL steps. Continue recording the total volume added and the measured pH following each addition on your data sheet.
- Observe the pH change after each addition carefully. At some point during your titration the pH difference between subsequent 0.5-mL additions will start to grow larger. Around this time, the pink color from the phenolphthalein indicator will also begin to persist in solution longer before vanishing. When you notice these changes slow down your addition rate to just 2 to 3 drops per addition. When the pH again begins to jump and you feel you are nearing the endpoint, slow down your addition rate to just 1 drop per addition. Continue to record the volume added and the pH after each addition.
- When the pink color from the phenolphthalein indicator persists for at least 2 minutes you have reached the endpoint of your titration. Note this point on your data sheet and stop the titration. In this experiment it is OK if you overshoot this mark by a few drops. (If you overshoot the endpoint by more than this you may need to repeat this titration, see your instructor for how to proceed).
- We now need to equalize the volumes in the two beakers labeled “HA” and “A- ”. Using your large graduated cylinder measure a volume of deionized water equal to the total amount of the 0.2 M \(\ce{NaOH}\) you added during your titration and add this volume of deionized water to the contents of the beaker labeled, “HA”. Swirl gently to mix.
- Using your large graduated cylinder measure out 25-mL of the solution from the beaker labeled “HA” and transfer this volume to your fourth clean rinsed 150-mL beaker. Label this beaker, “50-50 buffer mixture.”
- Now measure out 25-mL of the solution from the beaker labeled “A- ” and combine this with the solution in your beaker labeled “50-50 buffer mixture”. Swirl gently to mix. Using your pH meter, measure the pH of this solution and record the value on your data sheet.
- The pH of the solution in your beaker labeled, “50-50 buffer mixture,” is also the pKa of your unknown acid. Do you know why? You will need to tell your instructor this value for Part E.
- Save the remaining solutions in the beakers labeled, “HA” and “A–” and the beaker containing the remaining 0.2 M \(\ce{NaOH}\) solution for the next part of this experiment.
Part E: Buffer Solutions
Report the pKa value you determined for your unknown acid in Part D to your instructor who will assign you the pH value of the buffer solution you will prepare in this part of the experiment.
Now using the remaining solutions in the beakers labeled “HA” and “A- ”, prepare a buffer solution that will maintain the pH assigned to you by your instructor (see background section). It is suggested you use only a portion of each of these two solutions in case your first attempt does not succeed.
Use your pH meter to confirm the pH of your buffer solution. Your measured pH value should be within \( \pm 0.2\) pH units of your assigned value. Record your measured value on your data sheet and obtain your instructor’s initials confirming your success.
Now we will test the buffer solution you prepared against changes in pH.
- Rinse and fill another 150-mL beaker with a volume of deionized water equal to that of your buffer solution. Using your pH meter measure the pH of the deionized water. Do not be alarmed if this pH is less than neutral. It should be between 5.2 and 7.0. Do you know why? What species from the atmosphere dissolves in water that is left standing?
- Add 5 drops of the remaining 0.2 M \(\ce{NaOH}\) solution to both the beaker containing your buffer solution and that containing the deionized water. Measure the pH of each of these solutions following this addition and determine the change in pH of each. Record these values on your data sheet.
- Clean up. Discard all chemicals in the proper chemical waste container. Clean and then return all borrowed equipment to the stockroom.
Lab Report: pH Measurement and its Applications
Name: ____________________________ Lab Partner: ________________________
Date: ________________________ Lab Section: __________________
Part A – Determination of pH using Acid-Base Indicators
Record the colors of the indicators observed for each solution tested. Then use these colors and Table 1 to estimate the pH range of each solution (for example, pH =1-2):
| Indicator used | 0.1 M \(\ce{HCl}\) | 0.1 M \(\ce{NaH2PO4}\) | 0.1 M \(\ce{CH3COOH}\) | 0.1 M \(\ce{ZnSO4}\) |
|---|---|---|---|---|
| Methyl violet | ||||
| Thymol blue | ||||
| Methyl yellow | ||||
| Congo Red | ||||
| Bromcresol green | ||||
| pH range |
- Consider your results for the solutions of 0.1 M \(\ce{HCl}\) and 0.1 M \(\ce{CH3COOH}\). Which has the lower pH and why is its pH lower?
- Consider your results for the 0.1 M \(\ce{ZnSO4}\) solution. Is the solution acidic or basic? ____________
- Which ion, \(\ce{Zn^{2+}}\) or \(\ce{SO4^{2-}}\), is causing the observed acidity or basicity? ____________
- Write the net ionic equation below that shows why this ion is acidic or basic:
Part B – Using pH Meters
Record the measured pH and the color of bromcresol green indicator observed for each solution:
| 0.1 M \(\ce{NaCl}\) | 0.1 M \(\ce{Na2CO3}\) | 0.1 M \(\ce{CH3COONa}\) | 0.1 M \(\ce{NaHSO4}\) | |
|---|---|---|---|---|
| Measured pH | ||||
| Color in indicator |
- Consider your results for the 0.1 M\(\ce{NaCl}\) solution. Is the color obtained when tested with bromcresol green indicator as expected? Explain.
- Consider your results for the 0.1 M \(\ce{Na2CO3}\) solution. Is the solution acidic or basic?____________
- Which ion, \(\ce{Na^{+}}\) or \(\ce{CO3^{2-}}\) is causing the observed acidity or basicity?____________
- Write the net ionic equation below that shows why this ion is acidic or basic:
- Consider your results for the 0.1 M \(\ce{NaHSO4}\) solution. Is the solution acidic or basic?____________
- Which ion, \(\ce{Na^{+}}\) or \(\ce{HSO4^{-}}\) is causing the observed acidicity or basicity?____________
- Write the net ionic equation below that shows why this ion is acidic or basic:
- Write the chemical equation describing the equilibrium reaction between acetic acid and water:
Part C – Using pH to Determine the Value of \(K_{a}\) for Acetic Acid, \(\ce{CH3COOH}\) (aq)
Complete the following table. Use the known value of \(K_{a}\) for acetic acid from your textbook to determine the percentage error in your measured \(K_{a}\) value for each solution.
|
1.0 M \(\ce{CH3COOH}\) |
0.010 M \(\ce{CH3COOH}\) |
|
|---|---|---|
|
Measured pH |
||
|
\([\ce{H3O^{+}}]_{equil}\) |
||
|
\([\ce{CH3COO–^{-}}]_{equil}\) |
||
|
\([\ce{CH3COOH}]_{equil}\) |
||
|
\(K_{a}\) (calculated) |
||
|
\(K_{a}\) (textbook) |
||
|
Percent error |
- Show your calculations (using an equilibrium or ICE table) for obtaining the value of \(K_{a}\) for the 0.010 M solution (only):
Part D – Using a pH Titration to Determine the Value of Ka for an Unknown Acid
You only need to complete this table if your instructor chooses the OPTIONAL procedure for Part D.
|
Point |
Vol. \(\ce{NaOH}\) / mL |
pH |
Point |
Vol. \(\ce{NaOH}\) / mL |
pH |
|---|---|---|---|---|---|
|
1 |
0.00 mL (initial point) |
26 |
|||
| 2 | 27 | ||||
| 3 | 28 | ||||
| 4 | 29 | ||||
| 5 | 30 | ||||
| 6 | 31 | ||||
| 7 | 32 | ||||
| 8 | 33 | ||||
| 9 | 34 | ||||
| 10 | 35 | ||||
| 11 | 36 | ||||
| 12 | 37 | ||||
| 13 | 38 | ||||
| 14 | 39 | ||||
| 15 | 40 | ||||
| 16 | 41 | ||||
| 17 | 42 | ||||
| 18 | 43 | ||||
| 19 | 44 | ||||
| 20 | 45 | ||||
| 21 | 46 | ||||
| 22 | 47 | ||||
| 23 | 48 | ||||
| 24 | 49 | ||||
| 25 | 50 |
- Record your results below. Calculations do not need to be shown here.
- ID# of unknown weak acid: _____________
- Mass of unknown acid used: _____________
- pH of 50-50 buffer solution: _____________
- \(K_{a}\) of unknown weak acid: _____________ (from measurement of 50-50 buffer solution)
- (OPTIONAL) Use Excel to create a graph or titration curve of pH versus volume of 0.2 M \(\ce{NaOH}\) solution added for your pH titration data. Your graph should have an appropriate title and labeled axes with an appropriate scale. Referring to your textbook, locate and label the following points and regions on your graph: the initial point, the midpoint, the endpoint, and the buffer region. Use the value of the pH at the midpoint of your graph to determine the value of \(K_{a}\) for your unknown acid. Record this value below. Submit this graph with your report.
- \(K_{a}\) of unknown weak acid: ______________ (from midpoint of titration curve)
- How do you know the concentrations of \(\ce{HA}\) (aq) and \(\ce{A^{-}}\) (aq) were equal in the two solutions you mixed to form the 50-50 buffer solution? Explain your answer below in terms of chemical equations and the specific steps you took to ensure that this was the case:
- Using Equations \ref{3} and \ref{4} in the background section of this experiment, show that \(K_{a} = [\ce{H3O^{+}}]\) for the 50-50 buffer solution:
- (OPTIONAL) Is the endpoint of your pH titration that you marked on your titration curve the same as the equivalence point of the titration? Explain your answer:
Part E – Buffer Solutions
- Record your results below.
- pH of Buffer Assigned by Instructor: ______________
- Measured pH of Assigned Buffer: ______________
- Instructor’s Initials: _________
- Show the calculations you used and detail the steps you followed to prepare this buffer solution including the volumes of all solutions used:
- Compare the pH change of the buffer prepared above to that of deionized water upon the addition of a strong base by recording the following values:
| Deionized Water | Buffer Solution | |
|---|---|---|
| pH before adding \(\ce{NaOH}\) | ||
| pH after adding 5 drops \(\ce{NaOH}\) | ||
| pH change |
- Briefly explain why the buffer is more resistant to a change of pH upon addition of the base than the water. Use equations to support your explanation:
- Why isn’t the measured pH of the deionized water before adding the \(\ce{NaOH}\) (aq) equal to 7.0?
Pre-Laboratory Assignment: pH Measurement and Its Applications
- Solution X was tested with several acid base indicators and gave the following results: violet in methyl violet, yellow in thymol blue, yellow in methyl yellow, orange red in congo red and green in bromcresol green. What is its pH range? Explain your answer.
- Which of the following 0.1 M solutions will have the highest pH: acetic acid, \(\ce{HCl}\), ammonium chloride, \(\ce{NaH2PO4}\)? Explain your answer.
- You measure the pH of a 0.50 M unknown acid solution using a pH meter and it is found to be 1.74. What is \(K_{a}\) for the acid? Show your calculations.
- In part 4 of this experiment, you are asked to prepare a solution in which the concentration of a weak acid is equal to the concentration of its conjugate base. To produce the base, you titrate a portion of the weak acid with \(\ce{NaOH}\) to the end point of phenolphthalein. In the lab procedure, it was explained that the concentration of HA and A- are not equal at this point. How do you equalize these two concentrations?
- You find the \(K_{a}\) of your unknown acid is \(6.3 \times 10^{-5}\). If you are being asked to make a buffer at pH 4.00, what is the appropriate ratio of A- to HA to be combined in your flask?


