14B: Atomic Emissions Spectra - Pizza Box Version (Experiment)
- Page ID
- 95881
- To build and calibrate a simple box spectroscope capable of measuring wavelengths of visible light.
- To use this spectroscope to observe and measure the line spectra emitted by mercury, hydrogen, and other elements.
- To use Bohr’s theory to identify the electronic transitions that give rise to each wavelength observed in the line spectra of hydrogen.
Atomic Emission Spectra
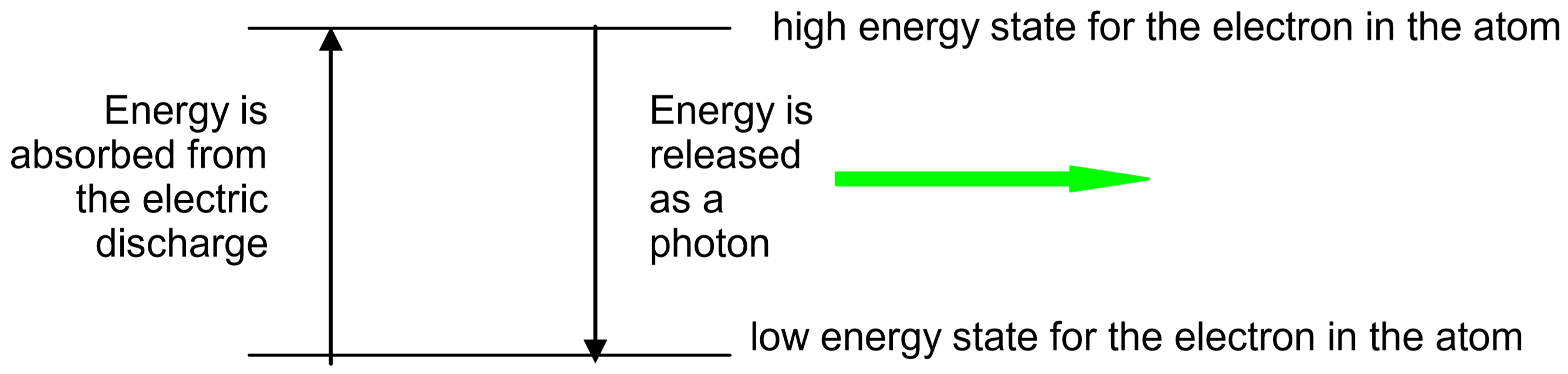
Electrons in atoms normally occupy the lowest energy states possible. Such an atom is said to be in the ground state. However, electrons can be excited to high energy states when they absorb energy. This energy can be provided by heat, light, or an electrical discharge. The electrons will then return to lower energy states, eventually returning all the way to the ground state. As the electrons return to lower energy states, they release their excess energy. Often, this energy is released in the form of light, with each atom or molecule releasing a single photon of light for each electron energy transition it makes.
For example, in the hydrogen discharge tubes used in this experiment the energy of the electric discharge first dissociates the \(\ce{H2}\) molecules into \(\ce{H}\) atoms, then excites the electrons in the \(\ce{H}\) atoms into high energy states. Due to conservation of energy, the amount of energy in an emitted photon will exactly match the amount of energy lost by the electron as it moves to the lower energy state.
Different colors of light are associated with different photon energies. For example, a single photon of blue light has more energy than a single photon of red light. Thus, the color of the light emitted by a particular atom depends upon how much energy the electron releases as it moves down to a lower energy level. The energy levels that are allowed for each atom depend upon the number and arrangement of protons and electrons in the atom. As each element has different energy states available to it, each element releases photons of different color when its atoms return to their lower energy states. Since each atom has many excited states (high energy levels) available to it, several colors of light can be emitted by each element. The set of individual colors emitted by an element is called its spectrum. Since the spectrum of each element is unique, spectra can be used like fingerprints to identify unknown elements.
Wavelengths of Light
Visible light is only one kind of electromagnetic radiation. The wavelength of radiation determines what kind of radiation it is. The human eye is able to detect only a narrow range of wavelengths of electromagnetic radiation, those from about 400 nm to about 700 nm. Radiation with wavelengths less than 400 nm includes ultraviolet, x-ray, or γ-rays, while radiation with wavelengths longer than 700 nm includes infrared radiation, microwaves, and radio waves. In this experiment, we use our eyes to detect the radiation emitted by excited atoms, and therefore we work only with visible light.
The color of light is related to its wavelength (\(\lambda\)), which is related to its frequency (\(\nu\)) and the energy of its photons (\(Ε\)). Shorter wavelengths of light have higher frequencies and higher photon energies while longer wavelengths of light have lower frequencies and less energy per photon.
It is easy to convert between photon energy, wavelength, and frequency using the following relationships
\[\lambda \nu = c\]
and
\[E = h \nu\]
Where \(c\) = the speed of light = \(2.998 \times 10^8 m/s\) and \(h\) = Planck’s Constant = \(6.626 \times 10^{-34} Js\). These two relationships combine to give a third:
\[E = \dfrac{hc }{\lambda}\]
Thus, the spectrum of an element can be stated by listing the particular wavelengths of light that its atoms emit.
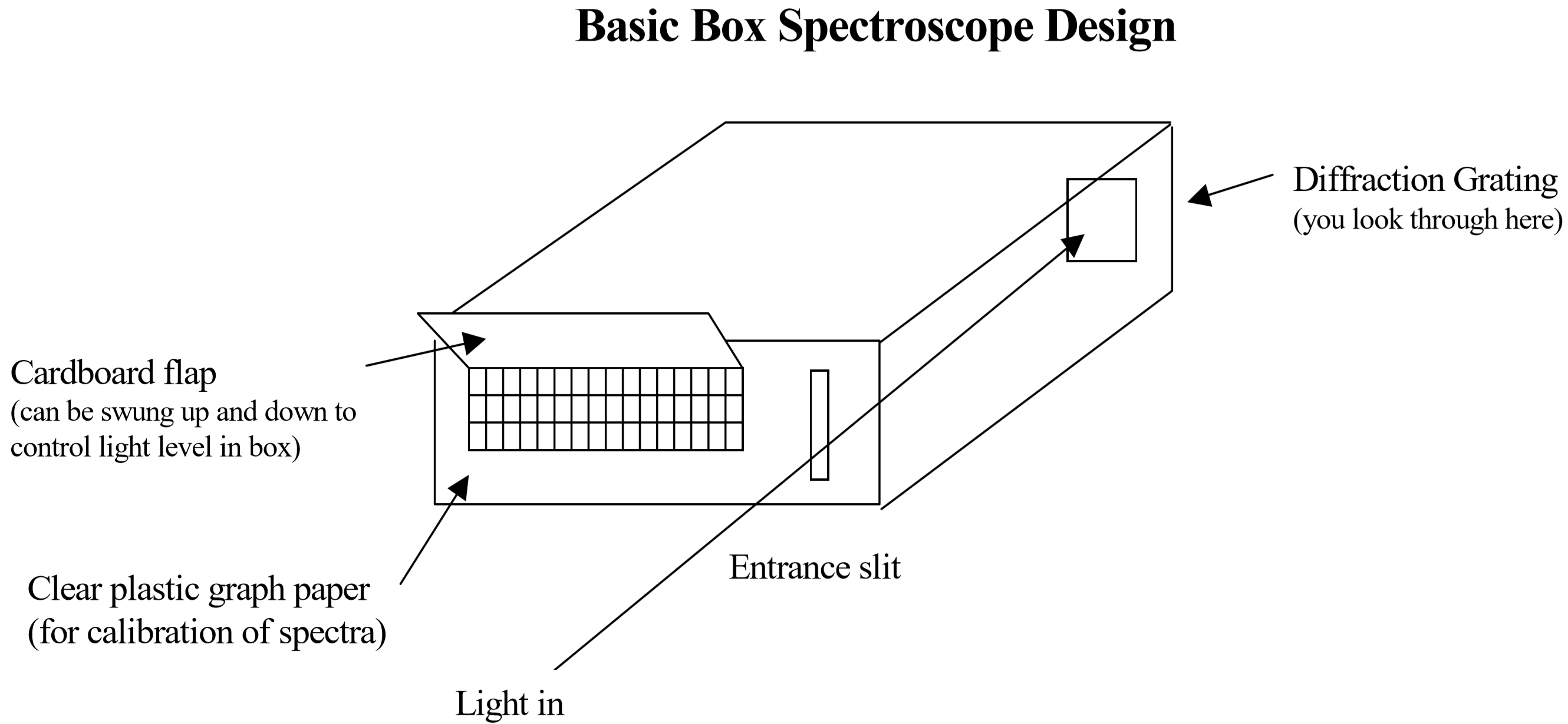
To measure these wavelengths in the laboratory, we must first separate them. To the naked eye, the various wavelengths (colors) of light emitted by an element are mixed together and appear as a single color that is a combination of the component colors. However, if we view the light through a prism or a diffraction grating, the individual wavelengths are separated. A diffraction grating is a piece of glass or clear plastic with many very narrow and closely spaced lines on it. As the light emerges after being reflected by the grating, these tiny lines cause the reflected light to interfere with itself in such a way that the different wavelengths of the light to appear in different positions to the left and right of the original direction in which the light was traveling. In this lab, a diffraction grating will be mounted in a simple “box spectroscope” that will be constructed by each student in lab.
Using a light source that contains known wavelengths of light, we can measure exactly where each known wavelength appears along a graph paper scale, which will be mounted opposite to the diffraction grating in the box spectroscope. Since this position has a linear dependence upon the wavelength, a graph of wavelength versus position of the spectral line will yield a straight line. Once the best fit straight line has been determined, the equation of this line can then be used to convert positions of other spectral lines to wavelength. For example, using the same box spectroscope, it is possible to view the spectrum of a new element, measure where its spectral lines occur on the graph paper scale, and then read the calibration graph (or use the equation of the line) to determine the wavelength to which each of those positions corresponds. The calibration graph is therefore an integral part of the spectroscope.
Bohr’s Theory
For atoms that contain only one electron, the theory of atomic structure proposed by Niels Bohr can be used to calculate wavelengths for transitions between particular electronic energy levels of the atom. In this experiment, the only one-electron atom we will consider is hydrogen. Note that there are other one-electron “atoms” if you consider ions such as \(\ce{He^+}\) and \(\ce{Li^{2+}}\). Using Bohr’s theory for hydrogen, a close match can be found between the calculated wavelengths and those measured experimentally. To calculate the wavelengths of light emitted by hydrogen atoms, recall that the energy of an electron in the nth energy level of a one-electron atom is given by:
\[E_n= -\dfrac{Z^2R}{n^2}\]
where \(R\) is the Rydberg constant = \(2.18 \times 10^{-18} J\), \(Z\) is the nuclear charge, and n = 1, 2, 3, ..., ∞. For hydrogen, the nuclear charge is 1 so this equation becomes:
\[E_n= -\frac{R}{ n^2}\]
The change in energy for the electron when it makes a transition from one level to another is given by its subtracting its initial energy from its final energy:
\[\Delta E_{\text{electron}} = E_f - E_i\]
By conservation of energy, the energy of the photon emitted as this electron drops to a lower energy level must equal the change in energy for the electron. However, since photon energies must be a positive quantity, the absolute value of the change in energy for the electron must be used:
\[E_{\text{photon}} = | \Delta E_{\text{electron}} |\]
Once the energy of the photon is known, it is readily converted into a wavelength as discussed earlier.
Because there are many energy levels possible for the electron in a hydrogen atom, and because the electron could jump from any higher n to any lower n, there are many lines in the spectrum of hydrogen. However, most of these lines occur at wavelengths which our eyes cannot detect (either infrared or ultraviolet). The visible portion of the spectrum which you will observe in this experiment was the first to be studied by scientists since it is the only portion which can be seen with the naked eye. This series of spectral lines is named for one of the first scientists to study it and is called the Balmer series. Note that all of the spectral lines in the Balmer series involve transitions from a higher n level to the n=2 level. You will need this information to complete the calculations for your lab report.
Procedure
Materials and Equipment
Medium-sized box supplied by each student (thinner cardboard is best), diffraction grating, strips of graph paper, box cutters, masking or black electrical tape, high voltage power supplies, hydrogen, mercury, helium and other polyelectronic element discharge lamps.
- Exercise extreme caution with the high voltage supplies as severe shocks are possible! Do not touch the front of the power supply while it is plugged in.
- Do not touch or attempt to remove the discharge tubes from the high voltage supplies. In addition to the risk of electrical shock, the tubes become very hot with use. The power supplies must be turned off and unplugged before changing discharge tubes.
- View the light emitted by the discharge tubes through glasses or goggles. Both glass and plastic lenses will absorb most of the harmful UV radiation emitted by many atoms.
Part A: Constructing and Calibrating a Box Spectroscope
Construction
Detailed instructions on how to construct and test the spectroscope will be provided at the beginning of the lab session. However the basic procedure is supplied here.
- Cut a hole for the grating and slit on opposite sides of the box. Use the wider sides of the box for your slit and grating, not the narrow sides.
- Mount the grating loosely and hold the box up to the light. Aim your spectroscope at a fluorescent ceiling lamp and look through the grating. You should see a spectrum (or rainbow) on the side (not top) of the box. If you do not see a spectrum on the side of the box, rotate the diffraction grating by 90 degrees.
- Note the approximate position of the spectrum and mark where it starts and ends on the box. Then cut out a cardboard flap on three sides slightly wider than this area. This is where you will be mounting the graph paper scale (see diagram).
- Use a pen to clearly label some of the lines on your graph paper strip: 1, 2, 3, etc. Write these numbers below the graph so that you can read them when the strip is mounted to the box. It does not matter whether you label each line 0, 1, 2, 3... or every 5th line, or every 10th line, just make sure that the spacing in your numbering scale is consistent.
- Tape the strip of graph paper over the space you just cut so that you can see the spectrum on the scale. With the flap slightly open you should be able to read the numbers that you wrote from inside the spectrometer.
- Finally, place a strip of black tape on either side of the hole where the light enters your box, narrowing it to a slit with a width of about 1 mm or less. Show your assembled spectroscope to your lab instructor before continuing.
- Test your spectroscope by aiming it at the fluorescent lights in the room. You should see a complete rainbow (a continuous spectrum) appearing clearly on the numbered portion of your scale. If not, consult with your instructor before continuing.
Calibration
- Aim your box spectroscope at one of the mercury emission lamps set up in the room. You should see four bright lines or spots on the scale: a deep violet or purple line, a bright blue line, a bright green line, and a bright yellow line (in that order). Note that the violet line can be hard to see and should be just beyond the bright blue line. The exact wavelengths of these four bright lines are given in the table below.
|
Color |
Wavelength |
|---|---|
|
Deep violet |
404.7 nm |
|
bright blue |
435.8 nm |
|
Bright green |
546.1 nm |
|
Bright yellow |
579.0 nm |
- Using Excel®, plot a graph of the exact wavelength of the four lines given above (in nm) versus their recorded positions on your spectroscope scale (in mm). Wavelength should be on the y-axis, position on the x-axis. Apply a trendline to this data and obtain the equation of this line. Your graph must be stapled to your report form.
This graph is called a calibration curve. It will allow you to find the exact wavelength of unknown spectral lines. Write the calibration equation on your spectroscope for easy reference, and record it on your Report Form as well. By using this equation you can easily convert a measured line position into a wavelength in nm.
Part B: The Spectrum of a Single Electron Atom – Hydrogen
- Now aim your box spectroscope at one of the hydrogen emission lamps set up in the room. Record the colors and positions of the lines you see on your Report Form, being careful to record them in the order they appear from left to right. You should see at least three lines clearly: red, aqua blue-green and deep indigo. You may also be able to see a deep violet line as well. When finished, use your calibration equation to determine the wavelengths of the each of the lines you observed.
- Using the equations of Bohr’s Theory, calculate the wavelengths of the first four lines in the Balmer series. Record your calculated results on your Report Form.
- Compare your calculated wavelengths with your measured wavelengths. Then identify which electronic transition ( from n = ?→ n = 2) is responsible for each of the lines you observed in the hydrogen spectrum. Calculate your percent error for each line, and record your results on your Report Form. Assume that the calculated wavelength is the actual, theoretical wavelength:
\[ \text{% error} = \frac{|\text{observed wavelength} - \text{actual wavelength}|}{\text{actual wavelength}} \times 100 \]
Part C: The Spectrum of a Polyelectronic Element
- Finally, aim your box spectroscope at either a helium lamp or one of the other polyelectronic element emission lamps set up in the room. Record the color of the six brightest spectral lines you see and their corresponding positions on the spectroscope. When you have finished, use your calibration equation to determine the wavelengths of the lines you observed.
- Use one of the lab computers to go to http://physics.nist.gov/PhysRefData/...ement_name.htm. Select the name of the element you chose, then click on the box labeled “Strong Lines”. Scan the wavelength column for the wavelengths you measured to see if you can find any close matches. Note the following:
- The tabulated wavelengths are given in units of Angstroms (1 A = 10-10 m). The wavelengths you have measured in lab are in nm (1 nm = 10-9 m). Thus, you must convert the numbers in the NIST table to nm by dividing them by 10. (i.e. 5890 A = 589.0 nm)
- Each element actually emits hundreds of wavelengths of light, but only some of those wavelengths are emitted with enough intensity (brightness) for our eyes to see them. The tabulated wavelengths include those that we cannot see with the naked eye, so you must scan down the “Intensity” column in the table of wavelengths to look for those lines that have high values for intensity. Look for those spectral lines that are significantly more intense than most since they are the ones you are likely to have seen in lab. Note that this means the wavelengths may not match perfectly.
- Record the tabulated wavelength for the intense line nearest to each wavelength you observed. Then calculate the % error for each of your measured wavelengths.
Pre-laboratory Assignment: Atomic Spectra
- Calculate the energy of the n=1 level for an electron in a hydrogen atom.
- Calculate the energy of the n=2 level for an electron in a hydrogen atom.
- Calculate the energy change when an electron in a hydrogen atom moves from n=2 to n=1.
- Calculate the wavelength of the light that an electron in a hydrogen atom would emit if it moved from n=2 to n=1.
- We can't see the light emitted by hydrogen atoms when the electrons move from any upper level to the n=1 level. Why not?
Lab Report: Atomic Emission Spectra
Part A: Construction and Calibration of the Spectroscope
Experimental Data
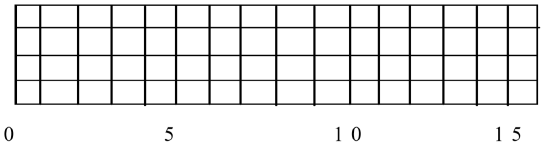
On the figure below, sketch in the observed line spectrum of mercury.
Record the following for the 4 brightest lines observed:
|
Line Color |
Spectral Line Position (mm) |
Actual Wavelength (nm) |
|---|---|---|
Data Analysis
- Using Excel, plot “Wavelength (Y) versus Spectral Line Position (X)”. Attach this graph to your lab report. Add a trendline to your data and obtain the equation for this best-fit line. Record this calibration equation below.
Calibration Equation:
- Would your calibration equation work for another person’s spectroscope? Why or why not?
Part B: Spectrum of a Single Electron Element – Hydrogen
Experimental Data
- • Record the following for the brightest lines observed (3 or 4):
|
Line Color |
Spectral Line Position (mm) |
Wavelength (nm) from Calibration Equation |
|---|---|---|
Data Analysis
- For the first four electronic transitions in the Balmer Series, calculate:
- the change in energy of the electron, \(\Delta E\)
- the predicted energy of the emitted photon, \(E_{\text{photon}}\)
- the predicted wavelength of the emitted photon, \(\lambda_{\text{photon}}\)
|
Electronic Transition |
\(\Delta E\) (J) |
\(E_{\text{photon}}\) (J) |
\(\lambda_{\text{photon}}\) (nm) |
|---|---|---|---|
|
n3 → n2 |
|||
|
n4 → n2 |
|||
|
n5 → n2 |
|||
|
n6 → n2 |
Clearly show the following calculations for the n3 → n2 transition:
- the change in energy of the electron, \(\Delta E\)
- the predicted wavelength of the emitted photon, \(\lambda_{\text{photon}}\)
- Based on your theoretical calculations, match the electronic transitions in the Balmer Series to the spectral lines you observed. Then calculate the percent error between your experimentally determined and calculated wavelengths.
|
Spectral Line Color Observed |
Experimental Wavelength (nm) |
Calculated Wavelength (nm) |
Electronic Transition |
Percent Error |
|---|---|---|---|---|
Below, clearly show your percent error calculation for the the the n3 → n2 transition.
- It is not possible to observe the n7 → n2 transition in the Balmer Series. Why is that?
Part C: Spectrum of a Polyelectronic Element
Experimental Data
Element name:
Record the following for up to 6 of the brightest lines observed:
|
Line Color |
Spectral Line Position (mm) |
Wavelength (nm) from Calibration Equation |
|---|---|---|
Data Analysis
- Go to the website: http://physics.nist.gov/PhysRefData/...ement_name.htm. Select the name of the element you chose, then click on the box labeled “Strong Lines”. Scan the wavelength column for the wavelengths you measured to see if you can find any close matches. Note the following:
- The tabulated wavelengths are given in units of Angstroms (1 A = 10-10 m). The wavelengths you have measured in lab are in nm (1 nm = 10-9 m). Thus, you must convert the numbers in the NIST table to nanometers before recording them below (divide by 10).
- Each element actually emits hundreds of wavelengths of light, but only a few are emitted with enough intensity (brightness) for our eyes to see them. The tabulated wavelengths include those that we cannot see with the naked eye, so you must scan down the “Intensity” column in the table of wavelengths. Look for those lines that have very high values for intensity compared to the rest – these are the ones you are likely to have seen in lab. Note that this means the wavelengths may not match perfectly.
Record the tabulated (actual) wavelength for the intense line nearest to each wavelength you observed. Then calculate the percent error for each of your measured wavelengths.
|
Spectral Line Color Observed |
Experimental Wavelength (nm) |
Actual Wavelength (nm) from website |
Percent Error |
|---|---|---|---|
- Why can’t the Bohr Theory be used to calculate the predicted wavelengths of emitted photons in the line spectra of polyelectronic elements?