Molecular Orbital Theory - LCAO (Dry Lab)

This exercise follows directly from the experiment on atomic orbitals that you have already done. The text that follows is not intended to be complete, but only a summary of material that should be covered in the lectures. The molecular orbital simulating program will be used several times.

Covalent Bonding in H₂

In studying atomic structure, you learned that a Schrödinger equation could be written for the hydrogen atom, and that this equation could be exactly solved. The previous exercise illustrated some of the solutions of this equation: the wave functions \(ψ\) (psi). Rather crude representations of the atomic orbitals called 1s and 2p are shown in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Remember that the sign (+ or -) shown on the figure has no physical significance, and simply indicates the sign of the numerical value of ψ in this region of space. Nevertheless, these signs are of importance.

It is a simple matter to write down the Schrödinger equation for a molecule. However, the resultant equation cannot be solved exactly except for the \(H_2^+\) ion. Various approximate methods are used to circumvent this difficulty. The one we will illustrated in this dry lab is called the molecular orbital (MO) approach. The objective is to answer the following questions:

1. What holds molecules together?
2. What are the electrons doing in the molecule?
3. What insight do these considerations give concerning the chemical and physical properties of the molecule?
4. Can we predict existence and structures of molecules?

The first objective is to derive molecular orbitals into which we can place all the electrons in the molecule in much the same way as we do for atoms. (Using the Aufbau Principle.) To obtain these molecular orbitals, we use a method called the linear combination of atomic orbitals (LCAO). As the name implies, the molecular orbitals are made by adding or subtracting the atomic orbitals. The simplest example is obtained by considering the hydrogen molecule, H₂, which we write as H_A-H_B, using the subscripts A and B to label the two atoms. LCAO theory states that one of the molecular orbitals can be written as:

\[ψ_1 = c_1 ψ_{1sA} + c_2 ψ_{1sB}\]

The constants c and d are weighting constants indicating the relative amounts of each atomic orbital that will be used. For H₂, where the two hydrogen atoms are equivalent, \(c_1 = c_2\), and we can replace them by a single "normalizing" constant \(N\):

\[ψ_1 = N(ψ_{1sA} + ψ_{1sB}) = \dfrac{1}{\sqrt{2}} (ψ_{1sA} + ψ_{1sB}) \label{1}\]

(If the probability of finding the electron in such an orbital somewhere in all space is to be equal to 1, N = 1/√2.)

So far we have done nothing difficult, but simply assumed that Equation \(\ref{1}\) represents our MO. Use the simulator to have a look at what this orbital looks like. You can adjust the distance between the nuclei to see what happens as the atomic orbital overlap more and more. Figure \(\PageIndex{2}\) gives a rather crude picture of what you should see.

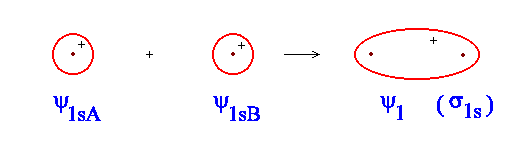
Figure \(\PageIndex{2}\): The constructive combination of 1s atomic orbitals combine to make the \(sigma_{1s}\) molecular orbital.

Since \(ψ_{1sA}\) and \(ψ_{1sB}\) are positive everywhere, their sum must be too. Just as for the atomic orbitals, the value of \(ψ^2\) gives the probability of finding the electron in a small region, or the electron density at a point. This particular orbital is referred to as a bonding molecular orbital for reasons that will shortly be explained.

There is another linear combination that we should have considered according to LCAO theory:

\[ψ_2 = \dfrac{1}{\sqrt{2}} (ψ_{1sA} − ψ_{1sB}) \label{2}\]

Use the simulator to have a look at what this combination looks like. Figure \(\PageIndex{3}\) shows a crude representation of what you should see. This combination is referred to as antibonding. Whenever we combine two atomic orbitals in a way which produces a change in the sign of ψ between the two component atomic orbitals, anti-bonding results.

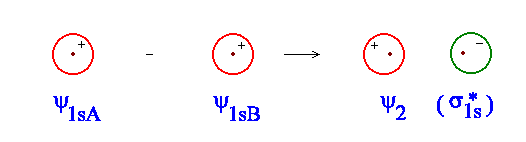
Figure \(\PageIndex{3}\): Construction of an antibonding molecular orbital.

We can better understand the difference between ψ₁ and ψ₂ by examining the electron density or probability. For the bonding combination this is given by:

\[ψ_1^2 = \dfrac{1}{2}\left( ψ_{1sA} + ψ_{1sB}\right)^2 = \dfrac{1}{2} \left(ψ_{1sA}^2 + ψ_{1sB}^2 + 2ψ_{1sA}ψ_{1sB}\right) \label{3}\]

If we compare this to the electron density contribution from two individual hydrogen atoms, ½(ψ_1sA² + ψ_1sB²), it is obvious that the electron density has been increased by a amount ψ_1sAψ_1sB. This effect, which accounts for the bonding because the negatively charged electrons hold the positively charged nuclei together, is illustrated in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\)

Example \(\PageIndex{1}\):

The probability plot for \(ψ_2^2\) is also shown in Figure \(\PageIndex{4}\). What would be its equation? (This is the equivalent of Equation \(\ref{3}\)) What do you notice about the electron density between the nuclei as compared to two individual hydrogen atoms simply placed side by side?

Solution

The equation would be:

\[ψ_1^2 = ½(ψ_{1sA} − ψ_{1sB})^2 = ½(ψ_{1sA}^2 + ψ_{1sB}^2 − 2ψ_{1sA}ψ_{1sB})\]

For this equation, the electron density is depleted between the two nuclei. The repulsion between them leads to the anti-bonding effect.

Further insight into the bonding of H_A and H_B can be obtained by considering the energies of the electrons in ψ₁ and ψ₂ compared to their energies in the non-interacting atoms. This can be done by plugging the LCAO wave functions for the molecule back into the appropriate Schrödinger equation (just as it can be done for the individual atoms using the atomic wave functions). The results are shown in Figure \(\PageIndex{5}\), where ψ₁ and ψ₂ are sometimes renamed σ(1s) and σ*(1s), respectively, to indicate the type of molecular orbital and their parentage.

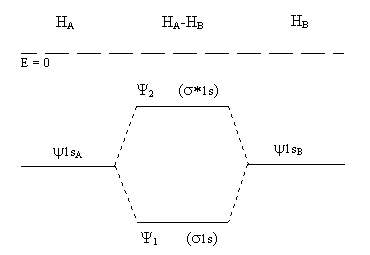
Figure \(\PageIndex{5}\)

These molecular orbitals are useful for any molecule, or molecule-ion, using only 1s orbitals for bonding. Several possibilities are: H₂⁺, H₂, H₂⁻, H₂²⁻, He₂⁺ and He₂. The positive molecule-ions are unstable, but have been detected in the gas phase under high energy conditions. The negative molecule-ions and He₂ have not been observed.

Example \(\PageIndex{2}\):

Using Figure \(\PageIndex{4}\), comment on the observations about the stability of the diatomic species listed above. (Would you expect all the negative molecule-ions to be unstable? Are there other species not listed which might be observed? Your answer should make reference to the electronic configuration and bond orders in these species.

Solution

Any species with a non-zero bond order might be observable.

Molecule/Ion	H2^+	H2	H2^−	H2^2−	He2^+	He2
Bond Order	½	1	½	0	½	0

Second-Row Homonulcear Diatomics

Second row atoms have 2s and 2p orbitals available for use in bonding. As in the case of two atoms with 1s orbitals interacting, two atoms with 2s orbitals interacting lead to two molecular orbitals called σ(2s) and σ*(2s).

The symbol σ is used when the molecular orbital has no nodal plane which contains both nuclei. For the bonding combination, there is only one region of high electron density between the two nuclei. If there is a single nodal plane containing both nuclei, the orbital is of type π. In this case, the bonding combination will have two regions of high electron density separated by the node. There are rare cases in certain transition metal compounds, where two nodes per molecular orbital contain both nuclei. These are designated d orbitals.

In valence bond theory terms, a single bond would have only a σ symmetry bond. A double bond consists of a σ and a π bond, a triple bond would have a σ and two π bonds, and the esoteric quadruple bond has one σ, two π and one d combination. In a multiple bond, the various orbitals co-exist in the same region of space between the nuclei. Do not mistake the two regions of overlap of a π-bonding orbital for a double bond!

Use the simulator to display the molecular orbitals derived from the 2s atomic orbitals on two atoms.

Example \(\PageIndex{3}\):

Prepare sketches of the σ(2s) and σ*(2s) orbitals similar to Figures \(\PageIndex{2}\) and \(\PageIndex{3}\). Do not attempt to copy all shading; just show all the nodes and the phase (sign) of ψ. Do they differ at all from Figures \(\PageIndex{2}\) and \(\PageIndex{3}\)?

Solution

The principal difference, which is actually of no real consequence, is the presence of the (now slightly distorted) spherical nodes which were present in the uncombined 2s orbitals. The 1s orbitals would have none. Otherwise the bonding orbital has somewhat increased electron density in the internuclear region, while the antibonding combination has less, exactly as is found for the σ(1s) and σ*(1s) orbitals, respectively.

Next use the simulator to display the overlap of two 2p_x orbitals. (The x axis is taken as the internuclear axis by the computer program.)

Example \(\PageIndex{4}\):

Prepare crude sketches of the resulting orbitals. Which combination, the sum or the difference, corresponds to the bonding combination this time? What would be the names for these orbitals?

Solution

The orbitals would be designated σ(2px) and σ*(2px) to indicate their "parentage", and the one with the minus sign would be the bonding combination this time. There is no single node passing through both nuclei, hence the σ designation.

Now use the simulator to examine the molecular orbitals that result from the linear combinations of the 2p_y orbitals. (Note that the results would be the same for the combinations of 2p_z orbitals, which, if you wish, you can check by varying the value of z.)

Example \(\PageIndex{5}\):

Once again prepare simplified sketches of what you see. Give the proper labels for the two combinations, including the * to indicate which is the antibonding orbital.

Solution

This time, the combinations have a node passing through both nuclei, so they are π orbitals. The bonding combination is their sum.

At this point you should have seen all the all the molecular orbitals formed by pairs of 2s and 2p orbitals. We can construct an energy level diagram to illustrate the relative energies of all these molecular orbitals and the atomic orbitals from which they are derived (Figure \(\PageIndex{6}\)).

Figure \(\PageIndex{6}\)

Example \(\PageIndex{6}\):

What is the bond order in Li₂ and O₂?

The answer should be accopanied by a diagram or some other explanation showing that Li₂ has a bond order of 1 (σ(2s)²) and O₂ a bond order of 2 (σ(2s)²σ*(2s)²σ(2p)²π(2p)⁴π*(2p)²). The students have been told that the bond order is:

(# bonding electrons - # antibonding electrons)/2

1. What homonuclear molecule-cation and molecule-anion species should have the same bond order as O₂? Consider cases between X₂²⁻ and X₂²⁺where X = Li to Ne.

   Any ion with 6 valence electrons like oxygen will do, i.e. N⁻ or F⁺ giving molecule ions N₂²⁻ and F₂²⁺. The molecule ions (C²⁻)₂ and (Ne²⁺)₂ would have the same configuration as well, though making them and detecting them would be quite a challenge!

2. Predict which two second-row elements are unlikely to give a diatomic molecule. Does simple Lewis bonding theory agree with your predictions?

   Anything with and equal number of bonding and antibonding electrons. Be₂ and Ne₂ are the only neutral species which would fit this criterion. Certainly Ne₂ is not known.

Figure 6 does not quite tell the whole story. It can be refined a little by considering some other types of combination. Use the simulator to examine the linear combination of a 2s orbital on one atom with a 2p_x orbital on the other.

Exercise \(\PageIndex{1}\)

Again sketch the results. There is no special way to label these combinations, but say if they are of type σ or π, and whether they are bonding or antibonding.

Use the simulator to form a combination of a 2s orbital on one atom with a 2p_y orbital on the other.

Example \(\PageIndex{1}\):

Sketch the resulting orbital. Can you classify this orbital as σ or π and bonding or antibonding? Explain. Go back to the beginning of this section if you are not sure.

Solution

The combination is called non-bonding (or symmetry forbidden). There is a region of constructive interference (bonding) and an equal region of destructive interference (non-bonding) between the atomic orbitals. The terms σ or π are not applicable.

Your answers to questions \(\PageIndex{7}\) and \(\PageIndex{8}\) should have convinced you that an LCAO of the type illustrated in question \(\PageIndex{1}\) is a reasonable combination, but that the other combination, described in question \(\PageIndex{8}\), is not useful. (Such a combination is called non-bonding.)

The results of including the additional overlap of 2s with 2p orbitals is shown in Figure \(\PageIndex{7}\). The main changes are shown in red.

• There is also a little contribution from the 2s orbitals to the most antibonding molecular orbital (at the top of the diagram), and a little contribution by the 2p orbitals to the most bonding molecular orbital (at the bottom).
• The main changes are that the orbital which was labelled σ(2p) and was below the π(2p) levels is now shown above the π(2p) and is now identified as σ*(2s,2p) while what was σ*(2s) has become σ(2s,2p).

The difference does not affect our predictions for any of the stable homonuclear diatomic molecules, but it does slightly change our predictions for some of the more exotic species such as B₂, which can be detected in boron vapour.

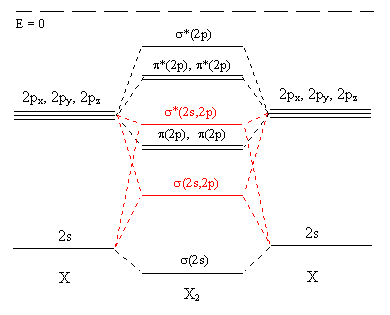
Figure \(\PageIndex{7}\)

In actual fact the extent of the 2s - 2p interaction changes from Li₂ to F₂, becoming gradually less important, so that we should use the "improved" diagram (Figure \(\PageIndex{7}\)) for Li₂ to N₂ and Figure \(\PageIndex{6}\) for O₂ F₂ (and cations of Ne₂). Figure \(\PageIndex{8}\) below shows what happens to the molecular orbitals as we cross the period.

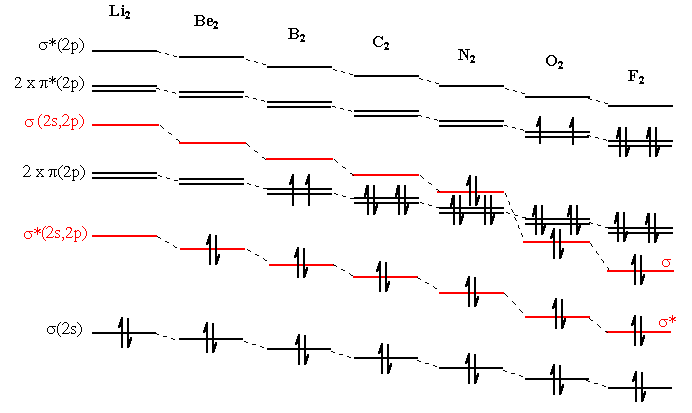
Figure \(\PageIndex{8}\)

Example \(\PageIndex{9}\):

What is the difference for B₂?

Solution

B₂ is paramagnetic when the π molecular orbitals lie below the σ molecular orbitals.

Example \(\PageIndex{10}\):

The questions, especially the third and fourth are very vague. In marking them, look for clear thinking and decent English. Take marks off for meaningless rambling!

Go back and briefly answer, in the context of the homonuclear diatomic molecules, the four questions which were posed at the beginning of this lab.

1. The covalent bond as described here is basically electrostatic. The negative electron density build-up between the positive nuclei results in the bond.
2. As in atoms, we cannot pin down the behaviour of the electrons. Molecular orbitals, like atomic orbitals tell us the probability of finding an electon in a certain region or a give us measure of electron density.
3. and 4. Pushed to much more quantitiative levels of theory than this lab, molecular orbital theory could allow us to predict charge densities on each atomic center and hence dipole moments and reactivities towards nucleophilic or electrophilic attack, but I think this question is just about the ability to predict the very existance or non-existance of diatomic molecules, and their bond orders (strengths) and magnetic properties.

Feel free to play with the simulator to examine some of the other combinations of atomic orbitals that are possible. Because the projection direction is down the z-axis certain combinations cannot be displayed.

Contributors

• Peter H. Bird (Department of Chemistry and Biochemistry, Concordia University, Montreal)