Density: Floating Footballs

On the television show "Mythbusters" Adam and Jamie tested out a myth that footballs filled with helium will fly further and hang longer than ones filled with regulation air. A likely source of the myth was Ray Guy, punter for the Oakland Raiders from 1973-86 ^[1]. Guy does not hold any distance records, but his punts stayed in the air so long that they invented the hangtime statistic for him. In a game against the Houston Oilers, he kicked it so well that the opposing team collected the ball and tested it. There was no helium.

Field Goal

The myth was busted; the football filled with air went farther. Nonetheless, the Mythbusters tested the hypothesis that helium-filled footballs travel farther than regulation footballs ^[2]. Faculty and students at several universities have gathered further evidence ^{[3] [4]}, trying to answer the question whether heavy footballs travel farther than light ones. Avogadro's principle states that an object is bouyed (or lifted up) by a force equal to the weight of the air displaced. What can a knowledge of density contribute to solving this riddle?

The terms heavy and light are commonly used in two different ways. We refer to weight when we say that an adult is heavier than a child. On the other hand, something else is alluded to when we say that air is heavier than helium. The mass of air in a tennis ball is much less than the mass of a roomful helium, but air is heavier in the sense that a given volume has a greater mass than the same volume of helium. We speak of mass in this case, because helium might be considered "weightless", since it floats in Earth's atmosphere (because air is pulled to the earth more strongly than helium is).

What we are actually comparing is the mass per unit volume, that is, the density. In order to determine these densities, we might weigh a cubic centimeter of each gas. If the air sample weighed 0.001185 g and the helium 0.00016 g, we could describe the density of air as 0.001185 g cm^–3 and that of helium as 0.00016 g cm^–3. (Note that the negative exponent in the units cubic centimeters indicates a reciprocal. Thus 1 cm^–3 = 1/cm³ and the units for our densities could be written as g/cm³, or g cm^–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate cm³ as "cc", and 1 cm³ = 1 mL by definition.

In general it is not necessary to weigh exactly 1 cm³ of a material in order to determine its density. We simply measure mass and volume and divide volume into mass:

\[\text{Density} = \dfrac{\text{mass}} {\text{volume}}\]

or

\[\rho = \dfrac{\text{m}} {\text{V}}\]

where

• ρ = density
• m = mass
• V = volume

Table \(\PageIndex{1}\) Densities of Common Gases

Substance	Density (g/cm^3 at 20^oC)
Hydrogen gas	0.000089
Helium gas	0.00018
Air	0.00128
Carbon Dioxide	0.001977
Sulfur hexafluoride	0.006164
Argon	0.0018
Halon 1301	0.0066
Water	1.00
Densities of many more materials are easily found.

Example \(\PageIndex{1}\) : Density Calculation

Calculate the density of (a) hot air weighing 0.0125 g trapped in a balloon which displaces 13.9 ml of water when submerged; (b) a sample of gas of mass 0.0612 g, trapped in an inverted cylinder of radius 0.750 cm, and height 5.25 cm in a pneumatic trough.

Solution

a) \(\text{Density} =\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{0.0125g} {13.9 mL} = \text {0.000899 g/mL or 0.000899 g mL}^{-1}\)

b) The volume of the cylinder must be calculated first, using the formula

\(\text{V} = {\pi} r^{2} h = 3.142 × \text{(0.750 cm)}^{2} * 5.25 \text{cm} = \text{9.278 718 8 cm}^{3}\)

Then \(\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{0.0612g} {9.278 718 8cm^{3}}\)

=\(\text{0.00660} \dfrac{\text{g}}{\text{cm}^3}\)

Note

Note that unlike mass or volume, the density of a substance is independent of the size of the sample. Thus density is a property by which one substance can be distinguished from another. A sample of pure air can have any desired volume or adjusted to have any mass we choose, but its density will always be 0.0001185 g/cm³ at 20°C. The densities of some common pure substances are listed in the Table.

Tables and graphs are designed to provide a maximum of information in a minimum of space. When a physical quantity (number × units) is involved, it is wasteful to keep repeating the same units. Therefore it is conventional to use pure numbers in a table or along the axes of a graph. A pure number can be obtained from a quantity if we divide by appropriate units. For example, when divided by the units gram per cubic centimeter, the density of aluminum becomes a pure number 2.70:

\[\dfrac{\text{Density of aluminum}} {\text{1 g cm}^{-3}} = \dfrac{\text{2.70 g cm}^{-3}} {\text{1 g cm}^{-3}} = 2.70\]

Table \(\PageIndex{2}\) Density of Several Substances at 20°C.

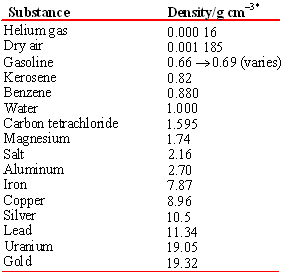
Therefore, a column in a table or the axis of a graph is conveniently labeled in the following form:

\[\dfrac{\text{Quantity}}{\text{units}}\]

This indicates the units that must be divided into the quantity to yield the pure number in the table or on the axis. This has been done in the second column of the Table.

What about the "floating football"? The Mythbusters found out that air in a football weighs about 3.2 grams ^[5]. This does not seem reasonable: If the air were at room temperature, 3.2 g would represent a volume of

\(\text{V} = \dfrac{m}{D} = \dfrac{\text{3.2 g}}{\text{0.001185} \dfrac{g}{cc}} = \text{2700 cc}\)

Footballs were inflated to 13 psi (over atmospheric pressure of 14.7 psi), and increasing the pressure from 14.7 to 27.7 psi would decrease the volume of air to 1433 cc. This seems too small for a football! The same volume of helium would weigh

\(\text{m} = \text{D} \times \text{V} = \text{0.00016} \dfrac{g}{cc} \times \text{2700 cc} = \text{0.432 g}\)

(using the density of helium and volume both at standard atmospheric pressure). The Mythbusters found that helium-filled footballs are 7 grams lighter than an air-filled ones, but their calculations seem incorrect. They claim that helium-filled footballs are lighter than an empty football by about 1% (not too far off), and that helium is only half as dense as air (incorrect; helium is 0.00016 /0.001185 X, or 0.14X the density of air). Nonetheless, they found experimentally, and others have verified, that helium filled footballs do not have longer hang times than regulation footballs.

Converting Densities

In our exploration of Density, notice that chemists may express densities differently depending on the subject. The density of pure substances may be expressed in kg/m³ in some journals which insist on strict compliance with SI units; densities of soils may be expressed in lb/ft³ in some agricultural or geological tables; the density of a cell may be expressed in mg/µL; and other units are in common use. It is easy to transform densities from one set of units to another, by multiplying the original quantity by one or more unity factors:

Example \(\PageIndex{2}\): Density Conversion

Convert the density of water, 1 g/cm³ to (a) lb/cm³ and (b) lb/ft³

a. The equality 454 g = 1 lb can be used to write two unity factors,

\(\dfrac{\text{454 g}} {\text{1 lb}}\) or \(\dfrac{\text{1 lb}} {\text{454}}\)

The given density can be multiplied by one of the unity factors to get the desired result. The correct conversion factor is chosen so that the units cancel:

\(\dfrac{\text{1 g}} {\text{cm}^{3}}* \dfrac{\text{1 lb}} {\text{454 g}} = 0.002203 \dfrac{\text{lb}} {\text{cm}^{3}}\)

b. Similarly, the equalities 2.54 cm = 1 inch, and 12 inches = 1 ft can be use to write the unity factors:

\(\dfrac{\text{2.54 cm}} {\text{1 in}}\), \(\dfrac{\text{1 in}} {\text{2.54 cm}}\), \(\dfrac{\text{12 in}} {\text{1 ft}}\) and \(\dfrac{\text{1 ft}} {\text{12 in}}\)

In order to convert the cm³ in the denominator of 0.002203 \(\dfrac{lb} {cm^{3}}\) to in³, we need to multiply by the appropriate unity factor three times, or by the cube of the unity factor:

\(\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\)

or

\(\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}\) x \((\dfrac{\text{2.54 cm}} {\text{1 in}})^{3} = \text{0.0361} \dfrac{\text{lb}}{\text{in}^3}\)

This can then be converted to lb/ft³:

\(\text{0.0361} \dfrac{\text{lb}} {\text{in}^{3}}\) x \((\dfrac{\text{12 in}} {\text{1 ft}})^{3} = \text{62.4} \dfrac{\text{lb}}{\text{ft}^3}\)

Note

It is important to notice that we have used conversion factors to convert from one unit to another unit of the same parameter

From ChemPRIME: 1.8: Density

References

1. en.Wikipedia.org/wiki/Ray_Guy
2. http://kwc.org/mythbusters/2006/02/mythbusters_catching_a_bullet.html
3. lib.stat.cmu.edu/DASL/Stories...mfootball.html
4. lib.stat.cmu.edu/DASL/Datafil...mfootball.html
5. http://kwc.org/mythbusters/2006/02/mythbusters_catching_a_bullet.html

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.