Synthesis of Superconductors

Equations and Mass Relationships in Physics

It's fairly easy to synthesize a superconductor, but to do so, you need to understand the principles of "stoichiometry". This is surprising, because superconductors are often materials that are considered "non-stoichiometric" berthollides^[1]. We'll explain below.

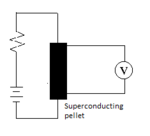
Superconductivity results in the famous Meissner Effect shown in the Figure or on YouTube. The effect is due to the expulsion of magnetic fields by superconductors, so they become perfectly diamagnetic^[2]. Superconductivity can be measured by the standard technique shown in the Figure, where the measured voltage drops to zero when the pellet is cooled below the "critical temperature".

Figure \(\PageIndex{1}\) The "Meissner Effect": Superconductor levitation

Figure \(\PageIndex{2}\) Measuring Superconductivity

The "1-2-3 Superconductor" the Bednorz and Müller synthesized may be the best known. It gets its name from it's formula, YBa₂Cu₃O_7-x, which shows that it contains 1 atom of Yttrium, 2 of barium, and 3 of copper. The number of oxygen atoms, "7-x", is variable, making the compound "nonstoichiometric", but stoichiometric principles are still necessary for its synthesis. The oxygen content depends on the atmosphere above the compound at various stages in its synthesis. The highest temperature superconductor is found for x = 0.15, where the "critical temperature", where superconductivity commences, is Tc = 92 K or -181 °C, and superconductivity disappears at x ≈ 0.6.

Present and Future Uses of Superconductors

Superconducting magnets are used in MRI and NMR machines, mass spectrometers, and in particle accelerators to focus particle beams. They are the building blocks of SQUIDs (superconducting quantum interference devices), the most sensitive magnetometers known. They may be used in advanced transportation, for efficient electric motors and magnetic levitation devices ^[3]. The 1987 Nobel prize was awarded to Bednorz and Müller at IBM Zurich for their discovery of superconductivity in copper containing oxides at over 30 K, and the search for higher temperature superconductors has been intense since that time.

Synthesis of a Superconductor

The 1-2-3 superconductor may be synthesized^[4] by mixing 0.60 g of yttrium oxide with "stoichiometric quantities" (see below) of barium peroxide and copper (II) oxide according to the equation:

\[\ce{2Y2O3 + 8BaO2 + 12CuO → 4 Y Ba2Cu3O6 + 5 O2} \label{1} \]

The YBa₂Cu₃O_7-x is prepared by grinding the reactants together, strongly heating "calcinating" at 900–950 °C for 8-12 hours, pelletizing the powder mixture, heating or "sintering" the pellet at 950 °C for 12 or more hours, then maintaining the product at 500°C for 12-16 hours. On slow cooling in oxygen atmosphere, YBa2Cu3O6 is converted to nonstoichiometric, superconducting YBa₂Cu₃O_7-x forms by uptake and loss of oxygen^[5].

But what does the phrase "stoichiometric quantities" in the procedure above mean?

A balanced chemical equation such as Equation \(\ref{1}\)

not only tells how many molecules of each kind are involved in a reaction, it also indicates the amount of each substance that is involved. Equation (1) says that 2 Y₂O₃ formula units can react with 8 BaO₂ formula units and 12 CuO formula units to give 4 YBa₂Cu₃O₆ formula Units and 5 O₂ molecules. Here we've used the term "formula unit" to indicate that the substance may not be a molecule, but rather an ionic compound or ["network crystal"]. A "formula unit" gives the composition of the substance without specifying the type of bonding.

Eq. (1) also says that 2 mol Y₂O₃ reacts with 8 mol BaO₂ and 12 mol CuO yielding 4 mol YBa₂Cu₃O₆ and 5 mol O₂.

The balanced equation does more than this, though. It also tells us that 2 × 4 = 8 mol Y₂O₃ will react with 2 × 8 = 16 mol mol BaO₂ and 2 × 12 = 24 mol BaO₂, and 2 × 12 = 24 mol CuO to give 2 × 4 = 8 mol YBa₂Cu₃O₆ and 2 × 5 = 10 mol O₂.

It also tells us that ½ × 4 = 2 mol Y₂O₃ requires only ½ × 8 = 4 mol BaO₂ and ½ × 12 = 6 mol CuO. to give ½ × 4 = 2 mol YBa₂Cu₃O₆ and ½ × 5 = 2.5 mol O₂. In other words, the equation indicates that exactly 8 mol BaO₂ must react for every 2 mol Y₂O₃ consumed. For the purpose of calculating how much BaO₂ is required to react with a certain amount of Y₂O₃ therefore, the significant information contained in Eq. (1) is the ratio

\(\dfrac{\text{8 mol BaO}_{2}}{\text{2 mol Y}_{2}\text{O}_{3}}\)

We shall call such a ratio derived from a balanced chemical equation a stoichiometric ratio and give it the symbol S. Thus, for Eq. (1),

\(\text{S}\left( \dfrac{\text{BaO}_{2}}{\text{Y}_{2}\text{O}_{3}} \right)~~ \) \(~~=\dfrac{\text{8 mol BaO}_{2}}{\text{2 mol Y}_{2}\text{O}_{3}}~~~~~\text{(2)} \)

The word stoichiometric comes from the Greek words stoicheion, “element,“ and metron, “measure.“ Hence the stoichiometric ratio measures one element (or compound) against another.

Example \(\PageIndex{1}\): Stoichiometric Ratio

Derive 4 additional stoichiometric ratios from Eq. \(\ref{1}\)

Solution: Any ratio of amounts of substance given by coefficients in the equation may be used:

\(\text{S}\left( \dfrac{\text{Y}_{2}\text{O}_{3}}{\text{O}_{\text{2}}} \right)=\dfrac{\text{2 mol Y}_{2}\text{O}_{3}}{\text{5 mol O}_{\text{2}}}~~~~~~ \)

\(\text{S}\left( \dfrac{\text{O}_{\text{2}}}{\text{CuO}} \right)=\dfrac{\text{5 mol O}_{\text{2}}}{\text{12 mol CuO}} \)

\(\text{S}\left( \dfrac{\text{Y}_{2}\text{O}_{3}}{\text{CuO}} \right)=\dfrac{\text{2 mol Y}_{4}\text{O}_{3}}{\text{12 mol CuO}}~~~~~~ \)

\(\text{S}\left( \dfrac{\text{O}_{\text{2}}}{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}} \right)=\dfrac{\text{5 mol O}_{\text{2}}}{\text{4 mol YBa}_{2}\text{Cu}_{3}\text{O}_{}} \)

\( \text{S}\left( \dfrac{\text{BaO}_{2}}{\text{CuO}} \right)=\dfrac{\text{8 mol BaO}_{2}}{\text{12 mol CuO}}~~~~~~ \)

There are several more stoichiometric ratios, each connecting any two reactants or products.

When any chemical reaction occurs, the amounts of substances consumed or produced are related by the appropriate stoichiometric ratios. Using Eq. (1) as an example, this means that the ratio of the amount of BaO₂ consumed to the amount of Y₂O₃ consumed must be the stoichiometric ratio S(BaO₂/ Y₂O₃):

\(\dfrac{n_{\text{BaO}_{2}\text{ consumed}}}{n_{\text{Y}_{2}\text{O}_{3}\text{ consumed}}} =\text{S}\left( \dfrac{\text{BaO}_{\text{2}}}{\text{Y}_{2}\text{O}_{3}} \right)" src=\dfrac{\text{8 mol BaO}_{\text{2}}}{\text{2 mol Y}_{2}\text{O}_{3}}\)

Similarly, the ratio of the amount of YBa₂Cu₃O₆ produced to the amount of Y₂O₃ consumed must be

S(YBa₂Cu₃O₆/Y₂O₃):

\(\dfrac{n_{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}\text{ produced}}}{n_{\text{Y}_{2}\text{O}_{3}\text{ consumed}}} =\text{S}\left( \dfrac{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}}{\text{Y}_{2}\text{O}_{3}} \right) =\dfrac{\text{4 mol YBa}_{2}\text{Cu}_{3}\text{O}_{6}}{\text{2 mol Y}_{2}\text{O}_{3}} \)

In general we can say that

\(\text{Stoichiometric ratio }\left( \dfrac{\text{X}}{\text{Y}} \right)=\dfrac{\text{amount of X consumed or produced}}{\text{amount of Y consumed or produced}}\text{ (3}\text{a)}\)

or, in symbols,

\(\text{S}\left( \dfrac{\text{X}}{\text{Y}} \right)=\dfrac{n_{\text{X consumed or produced}}}{n_{\text{Y consumed or produced}}}\text{ (3}\text{b)}\)

Note

Note that in the word Eq. (3a) and the symbolic Eq. (3b), X and Y may represent any reactant or any product in the balanced chemical equation from which the stoichiometric ratio was derived. No matter how much of each reactant we have, the amounts of reactants consumed and the amounts of products produced will be in appropriate stoichiometric ratios.

Example \(\PageIndex{2}\): Amount of Product

Find the amount of YBa₂Cu₃O₆ produced when 3.68 mol Y₂O₃ is consumed according to Eq. \(\ref{1}\).

Solution: The amount of YBa₂Cu₃O₆ produced must be in the stoichiometric ratio S(YBa₂Cu₃O₆//Y₂O₃) to the amount of Y₂O₃ consumed:

\(\text{S}\left( \dfrac{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}}{\text{Y}_{2}\text{O}_{3}} \right) =\dfrac{n_{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}\text{ produced}}}{n_{\text{Y}_{2}\text{O}_{3}\text{ consumed}}}\)

Multiplying both sides n_{Y2O3 consumed}, by we have

\(n_{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}\text{ produced}}~~=~~n_{\text{Y}_{2}\text{O}_{3}\text{ consumed}}~~\times~~\text{S}\left( \dfrac{\text{YBa}_{2}\text{Cu}_{3}\text{O}_{6}}{\text{Y}_{2}\text{O}_{3}} \right)\)

\(=~~\text{3.68 mol Y}_{2}\text{O}_{3}~~\times~~\dfrac{\text{4 mol YBa}_{2}\text{Cu}_{3}\text{O}_{6}}{\text{2 mol Y}_{2}\text{O}_{3}}~~=~~\text{7.36 mol YBa}_{2}\text{Cu}_{3}\text{O}_{6}\)

This is a typical illustration of the use of a stoichiometric ratio as a conversion factor. Example 2 is analogous to Examples 1 and 2 from Conversion Factors and Functions, where density was employed as a conversion factor between mass and volume. Example 2 is also analogous to Examples 2.4 and 2.6, in which the Avogadro constant and molar mass were used as conversion factors. As in these previous cases, there is no need to memorize or do algebraic manipulations with Eq. (3) when using the stoichiometric ratio. Simply remember that the coefficients in a balanced chemical equation give stoichiometric ratios, and that the proper choice results in cancellation of units. In road-map form

or symbolically.

\(n_{\text{X consumed or produced}}\text{ }\overset{S\text{(X/Y)}}{\longleftrightarrow}\text{ }n_{\text{Y consumed or produced}}\)

When using stoichiometric ratios, be sure you always indicate moles of what. You can only cancel moles of the same substance. In other words, 1 mol Y₂O₃ cancels 1 mol Y₂O₃ but does not cancel 1 mol YBa₂Cu₃O₆.

The next example shows that stoichiometric ratios are also useful in problems involving the mass of a reactant or product.

Example \(\PageIndex{3}\) : Mass Required

Calculate the mass of BaO₂ required when 3.68 mol Y₂O₃ is consumed according to Equation \(\ref{1}\).

Solution: The problem asks that we calculate the mass of BaO₂ consumed. As we learned in Example 2 of The Molar Mass, the molar mass can be used to convert from the amount of BaO₂ to the mass of BaO₂. Therefore this problem in effect is asking that we calculate the amount of BaO₂ consumed from the amount of Y₂O₃ consumed. This is the same kind of problem as in Example 2. It requires the stoichiometric ratio

\(\text{S}\left( \dfrac{\text{BaO}_{\text{2}}}{\text{Y}_{2}\text{O}_{\text{3}}} \right)=\dfrac{\text{8 mol BaO}_{\text{2}}}{\text{2 mol Y}_{\text{2}}\text{O}_{3}}\)

The amount of BaO₂ consumed is then

\( n_{\text{BaO}_{\text{2}}}\text{ consumed} ~=~n_{\text{Y}_{2}\text{O}_{\text{3}}\text{ consumed}}~~\times~~\text{ conversion factor} ~=~\text{3.68 mol Y}_{2}\text{O}_{3}~\times~\dfrac{\text{8 mol BaO}_{2}}{\text{2 mol Y}_{2}\text{O}_{3}} \)

The mass of BaO₂ is

\(\text{m}_{\text{BaO}_{\text{2}}}=\text{14.72 mol BaO}_{\text{2}}~\times~ \dfrac{\text{169.33 g BaO}_{\text{2}}}{\text{1 mol BaO}_{\text{2}}}=\text{2493 g BaO}_{\text{2}}\)

With practice this kind of problem can be solved in one step by concentrating on the units. The appropriate stoichiometric ratio will convert moles of Y₂O₃ to moles of Y₂O₃ and the molar mass will convert moles of BaO₂ to grams of BaO₂. A schematic road map for the one-step calculation can be written as

\(n_{\text{Y}_{2}\text{O}_{\text{3}}}~~\xrightarrow{S\text{(BaO}_{\text{2}}\text{/Y}_{\text{2}}\text{O}_{3}\text{)}}~~n_{\text{BaO}_{\text{2}}}~~\xrightarrow{M_{\text{BaO}_{\text{2}}}}~~m_{\text{BaO}_{\text{2}}}
\)

Thus

\(\text{m}_{\text{BaO}_{\text{2}}}~~=\text{3}\text{.68 mol Y}_{\text{2}}\text{O}_{3}~\times~\dfrac{\text{8 mol BaO}_{\text{2}}}{\text{2 mol Y}_{\text{2}}\text{O}_{3}}~~\times~\dfrac{\text{169.33 g}}{\text{1 mol BaO}_{\text{2}}}=1.56g ~\ce{BaO2}\)

These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. You may verify the additional calculations.

	2 Y2O3	+ 8 BaO2	+ 12 CuO →	4 YBa2Cu3O6	+ 5 O2
m (g)	831.0	2493	1757	4786	294.4
M (g/mol)	225.81	169.33	79.55	650.2	32
n (mol)	3.68	14.72	22.08	7.36	9.20

Example \(\PageIndex{4}\): Mass of Reactants

The highest temperature superconductor synthesized so far is HgBa₂Ca₂Cu₃O_8+x with T_c = 134 K.

Although the synthesis is more complicated^[6][7] then the one above, we can explore the stoichiometry, as usual, by writing an equation for the synthesis of the stoiciometric compound HgBa₂Ca₂Cu₃O₈. The stoichiometric compound is heated in oxygen to produce the nonstoichiometric superconductor.

HgO + 2 BaO₂ + 2 CaO + 3 CuO → HgBa₂Ca₂Cu₃O₈ + O₂

Prepare a table like the one above, calculating the amount and mass of each reactant necessary to consume 1 g of HgO, and the amount and mass of products formed.

Solution:

The problem gives the mass of HgO and asks for the amounts and masses of other reactants and products. Thinking the problem through before trying to solve it, we realize that the molar mass of HgO could be used to calculate the amount of HgO consumed. Then we need stoichiometric ratios to get the amounts of other reactants and products. Finally, the molar masses of permit calculation of the masses. Symbolically, for the reactant BaO₂,

\(m_{\text{HgO}}~~\xrightarrow{M_{\text{HgO}}}~~n_{\text{HgO}}~~\xrightarrow{S\text{(BaO}_{\text{2}}\text{/HgO)}}"~~\text{ }n_{\text{BaO}_{\text{2}}}~~\xrightarrow{M_{\text{BaO}_{\text{2}}}}\text{ }m_{\text{BaO}_{\text{2}}}m_{\text{BaO}_{\text{2}}}\)

\(m_{\text{BaO}_{\text{2}}}~~=\text{1.00 g}~\times~\dfrac{\text{1 mol HgO}}{\text{216.6 g}}~~\times ~~\dfrac{\text{2 mol BaO}_{\text{2}}}{\text{1 mol HgO}}~~\times ~~\dfrac{\text{169.33 g}}{\text{1 mol BaO}_{\text{2}}}~~=~~\text{1.56 g} \ce{BaO2} \)

	1 HgO	+ 2 BaO2	+ 2 CaO	+ 3 CuO →	1 HgBa2Ca2Cu3O8	+ 1 O2
m (g)	1.00	1.56	0.518	1.11	4.04	0.148
M (g/mol)	216.6	169.33	56.08	79.55	874.0	32
n (mol)	0.00462	0.00923	0.00923	0.0139	0.00462	0.00462

Make sure you can do these calculations, and show that the sum of the masses of the reactants equals the sum of the masses of products as a final check.

From ChemPRIME: 3.1: Equations and Mass Relationships

References

1. ↑ http://arxiv.org/PS_cache/cond-mat/pdf/0311/0311265v2.pdf
2. ↑ en.Wikipedia.org/wiki/Meissner_effect
3. ↑ en.Wikipedia.org/wiki/Superconductor
4. ↑ materials.binghamton.edu/labs...er/superc.html
5. ↑ en.Wikipedia.org/wiki/Superconductor
6. ↑ Yoo, S. H.; Wong, K. W.; Xin, Y. Physica C: Superconductivity, Volume 273, Issue 3-4, p. 189-192 (1996)
7. ↑ Wu, X. S. Shao, H. M. Yao, X. X. Jiang, S. S. Wang, D. W. Wu, Z. H. Cai, Y. M. Shen, L. J. Wu, Z. Synthesis of the superconducting thin film of HgBa2Ca2Cu3O8+δ. Applied Physics Letters 68(12) 1723-1725 (1996)

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.